実は「円描写プロセスの理論化」は近世以降の数学・物理学の最大の成果とも。
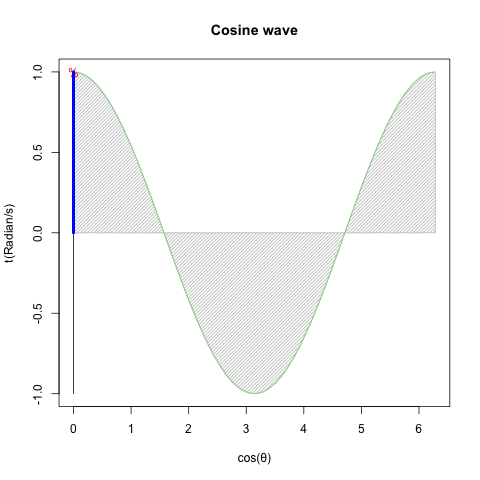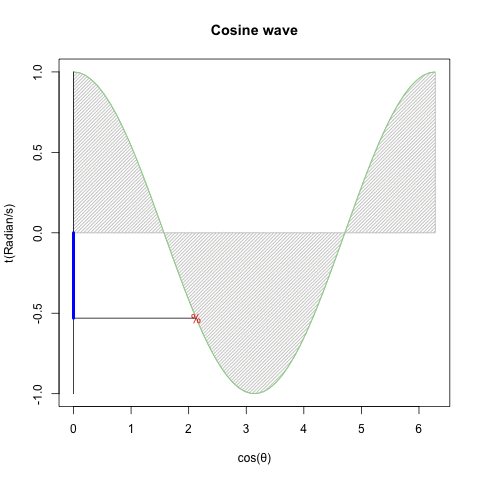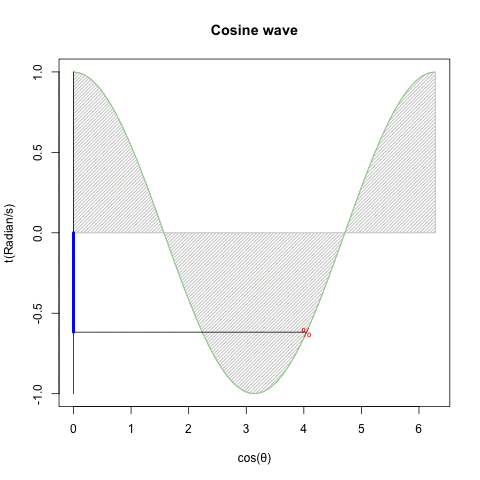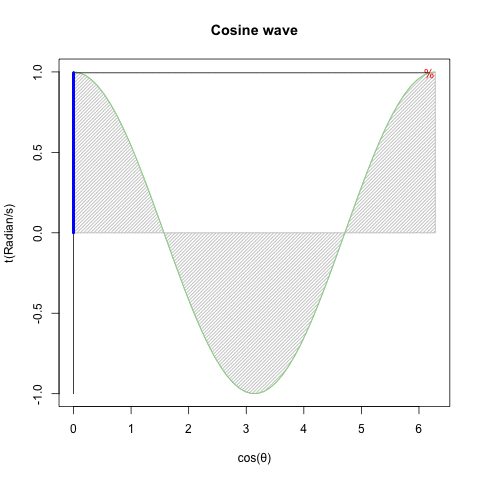
①等速円運動(Constant velocity circular motion)をX軸から観察すればCos波が、Y軸から観察すればSin波が得られる。②すなわちX軸にCos波、Y軸にSin波を配置すれば円が描かれる。
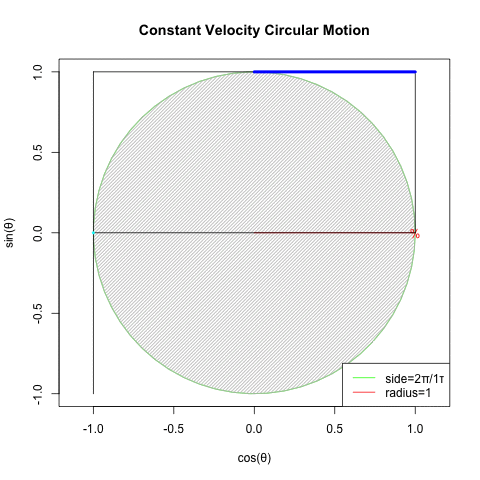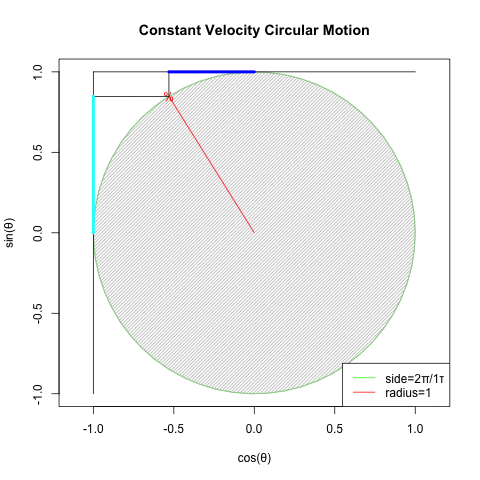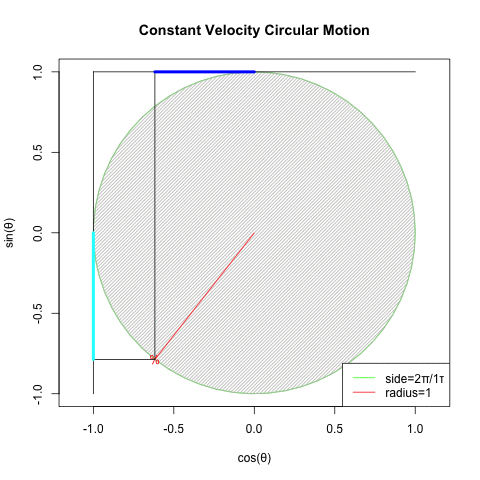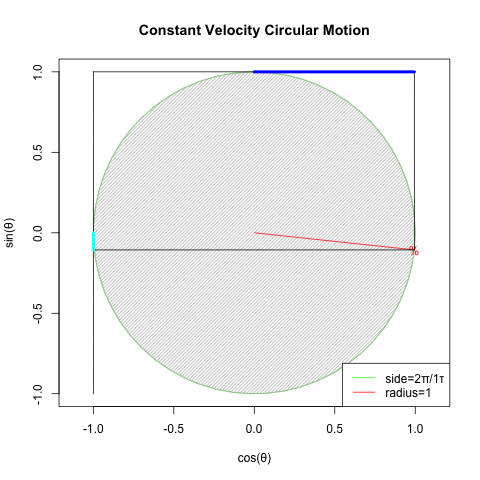

②物理学者や天文学者がこのシンプル極まりない、ある意味当たり前といえば当たり前過ぎる数理モデルを何時から採用してきたかは不明だが、一般的には不可逆的な形でコンセンサスとして共有される様になったのは概ね、初めてバネの伸縮の振動運動的周期性を力学的に規定したフックの法則(Hooke's law、1676年〜1678年)f=kxの発表以降と考えられている。
③この概念を関数Y=f(X)のフォーマットに落とし込む為、数学者は(2乗すると-1となる)虚数(Imaginary number)iなる概念を方便として新設し、これを指数とする冪乗関数X^iがCos波の様な偶関数の返り値が実数域、Sin波の様な奇関数の返り値が虚数域に振り分けられる性質を利用して複素平面(Complex plane)に円を描く技法を編み出した。ここに初登場を果たした「2乗すると-1となる」虚数(Imaginary number)iなる概念についての理解は、とりあえず「その関数内に含まれる(Cos波などの)偶関数をX軸=実数軸、(Sin波などの)奇関数をY軸=虚数軸に割り振ってくれる便利な判別フィルター」程度で良い。
*実は上掲の物理学や天文学の世界における方便、逆にかかる数学上の発見をそちらの世界に導入すべく発明されたとする考え方すら存在する。そもそもこうした研究の先人達は概ね数学者にして物理学者にしてや天文学者だったので、もう本当にどうやってコンセンサスが形成されてきたか判別が難しい。

*一般にはラプラス(Pierre-Simon Laplace, 1749年〜1827年)やガウス(Carolus Fridericus Gauss、1777年〜1855年)辺りが「犯人」と目されている。
こういう話をすると多くの人間がオイラーの公式(Euler's formula、1748年発表)e^θi=Cos(θ)+Sin(θ)i(理論値)=(1±θi/N)^N(ベルヌーイ大数弱の法則による到達不可能性の明示)を連想するし、実際そういう話なのですが、最もミニマムな形式は振動関数-1^θ(この形式のままだと実数領域に連続的に展開出来ない)=-1i^2^θ(-1に-1i^2を代入)=-1i^2θ(オイラーの公式同様に半径1の円を描くが、Sin波とCos波の周期はあくまで「2」。ちなみにこれはオイラーの公式e^θiを実際に描くSin波とCos波の周期も同様である)に現れるので、このサイトではこちらを採用しています。