
実は代数方程式(Algebraic formula)と超越方程式(Transcendental formula)の境界線を巡る議論がどの資料を見てもチンプンカンプン…
代数方程式でないすべての方程式をいう。対数方程式,指数方程式,三角方程式などは超越方程式である。
超越曲線(transcendental curve)とは代数曲線(algebraic curve)、特にユークリッド幾何学における平面代数曲線 (plane algebraic curve)でないもの,すなわちその曲線を表わす代数方程式 f(x,y)=0が存在しない曲線をいう。たとえば,指数曲線,対数曲線,サイクロイド,アルキメデスのスパイラル,正弦曲線,余弦曲線,正接曲線などは超越曲線である。
超越関数(Transcendental function) - Wikipedia
多項式方程式を満たさない解析関数であり、代数関数と対照的である。言い換えると、超越関数は加算、乗算そして冪根という代数的演算を有限回用いて表せないという意味で代数を「超越」したものである。
超越関数の例として、指数関数、対数関数、そして三角関数が挙げられる。
正式には、実あるいは複素変数 z の解析関数 f(z) が超越的とは、f(z) が z と代数的独立であることをいう。この定義は多変数関数にも拡張できる。
関数を大きく代数関数と超越関数に分けるのはなぜかというと、曲線の世界が代数曲線と超越曲線に区分けされているからです。代数曲線を代数関数のグラフとして把握したいのと同様に、超越曲線は超越関数のグラフとして把握したいというのがオイラーの数学的意図なのですが、超越曲線というものの正体が不明瞭なだけに、超越関数の姿もまたなかなか明確になりません。超越曲線というのは代数的ではない曲線というほどのことで、具体的な事例を挙げると、正弦曲線や余弦曲線、対数曲線、サイクロイドなどは超越曲線です。ですが、具体例をどれほど書き並べても、それだけでは超越曲線の一般概念を把握するにはいたりません。
超越曲線とは非代数的曲線のこととのみ理解するのであれば、それに対応して、超越関数もまた代数的ではない関数とのみ言うほかはありません。オイラーはいろいろな例を挙げていますが、sin x、cos x、tan x、e^x、log xなどを解析的表示式の仲間に入れてこれらを関数と呼ぶことにすれば、既知の超越曲線はたいてい超越関数のグラフとして認識されます。それでも関数の一般概念をはじめ代数関数についても超越関数についても今日のいわゆる厳密な定義は表明されていないのですから、その点を指摘して、オイラーは厳密ではないと批判する余地は確かにあります。ですが、オイラーには「曲線を関数のグラフとして認識する」というアイデアがあり、このアイデアを具体化しようとして関数の概念を模索しているのですから、オイラーにとってこの批判は意味をなさないと思います。
で、とりあえず代数方程式(Algebraic formula)とは何かについて自分なりにまとめてみたのが以下。
この考え方で正しいのなら超越方程式の骨子は「代数的演算(Algebraic operations、加減算、乗除算、冪根)を有限回用いて表せる表現」に収まらない事を指している事になります。で、著名なオイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θi)はそうした関数の関連性を証明して一つにまとめる壮大な構想の一部だったらしいのです…
①「X軸にCos(θ)波、Y軸にSin(θ)波を配すれば円弧が描画される」認識自体は等速円運動の解析からも得られるとされている。当然周期は円周分の2πとなる。
②ならばどうやって自然対数関数もCos(θ)波とSin(θ)に分解可能と気付いたか。それを可能とするのが(高階微分を応用した)テイラー/マクローリン級数や(正弦波の足し合わせによってあらゆる波形を再現する)フーリエ変換といった近似技法であり、実際オイラーの研究もテイラー/マクローリン級数の存在を知って習得して以降、急速に捗っている。ちなみに後者の周期は当然円周分の2πなのだが前者のそれは「微積分4連続分」としか分からない。
③次はどうやって一つの波形からCos(θ)波の様な偶関数とSin(θ)波の様な奇関数を分離するかだが、マクローリン級数の解析結果からも符号を調整すべきなのがSin(θ)波の方だったのは明らかで、既に百年以上前に発見されていた虚数に奇関数にだけ働く特徴がある事にも自然に気付いたと考えられている。かくしてオイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θi)そのものは成立した。
④表現を濁したのはマクローリン級数の近似値をそのまま複素空間に持ち込んでもちゃんと円を描かない事を知ってるから。複素平面の発明や1の冪根と単位円の関係を含め複素数にまつわる数理の多くはガウスが整備したのである。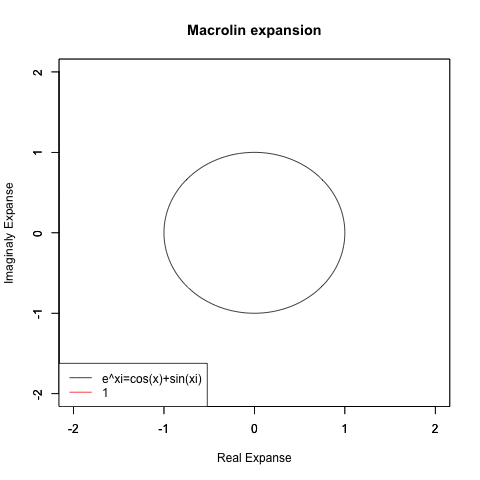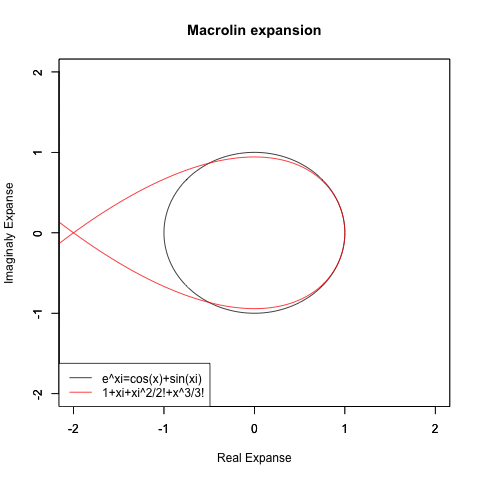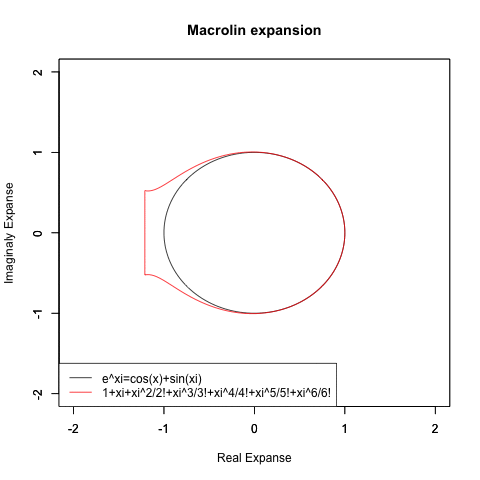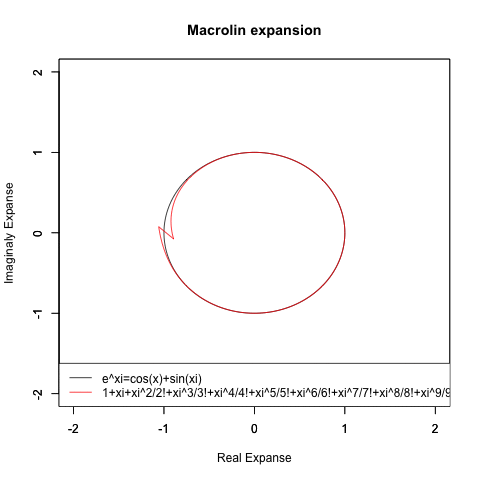
④ところで1572年にイタリア人数学者ボンベリの手でi^2=-1と定義された虚数は、振動関数-1^xに代入して-1i^2xの形に変形しても円を描くが、この時観測されるCos(θ)やSin(θ)波の周期は(e^θi関数同様に)2となる(-1と1の往復)。
⑤そもそも挟み撃ち法などによって近似される単位円の円周長2πはどちらかというと定数的扱い。それがe^θiと打ち消しあうという事は、この式の本来の形たる(無限大から無限小にかけての数直線上における)方程式(1±θi/N)^Nと(無限小の辺長の辺を無限大に有する)円そのもの(Circle itself)を表す方程式cos(θ-π/N)*Nがある種の逆数関係にある事を示唆している様にも見えるのである。
とりあえず以下続報…