
テイラー展開は展開の中心付近の近似は良いのですが,ある区間においてテイラー展開式の部分和で近似しようとすると,あまり良い近似式にならない場合があります.それで,関数を多項式関数や有理関数(多項式関数では不十分な場合もあります)による最良近似式を求めるための理論があり,実際に求められています.たとえば,「Computer Approximations, J.F.Hart etc , John Wiley & Sons.」には,100ページ以上にわたって,初等関数以外にガンマ関数,誤差関数,ベッセル関数,完全楕円積分等の最良近似多項式や最良近似有理式の表がのっています.
このようなことを最初に述べたのは,コンピュータで関数の数値計算をするときに,テイラー展開だけで十分だと思っていると思われる人がいるからです.もちろん,テイラー展開を用いた数値計算が役に立たないということではありません.(注) 近似式の理論に興味ある人は「近似式,一松信,竹内書店」を是非みて下さい.この本は残念ながら絶版ですので,大学の図書館もしくは数学科の図書室等で借りるしかないようです.気が向いたら解説しようと思っています.
とりあえず初学者なので、その多項式関数(Polynomial function)からテイラー展開/マクローリン展開を導出する最初歩の部分をやってみたいと思います。
統計言語Rによる実習
#多項式関数(Polynomial function)…とりあえず大学入試などで出る5次関数まで扱って残りは残余項とする。
PF00<-function(x,a0,a1,a2,a3,a4,a5,aN,N){a0+a1*x+a2*x^2+a3*x^3+a4*x^4+a5*x^5+aN^N}
#X軸フォーマット
glaph_x<-seq(-50:50,length=300)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"#タイトル定義
Main_title<-c("Polynomial function")
x_title<-c("X")
一次関数y=a1*x+a0あるいはa0の影響範囲
#グラフのスケール決定
gs_x<-c(-50,50)
gs_y<-c(-50,50)
#Y軸タイトル決定
y_title<-c("Y=a1*X+a0")
#y=x
f1_name<-c("y=x")
glaph_y1<-PF00(glaph_x,0,1,0,0,0,0,0,0)#y=x+10
f2_name<-c("y=x+10")
glaph_y2<-PF00(glaph_x,10,1,0,0,0,0,0,0)
#y=x-10
f3_name<-c("y=x-10")
glaph_y3<-PF00(glaph_x,-10,1,0,0,0,0,0,0)#y=-x
f4_name<-c("y=-x")
glaph_y4<-PF00(glaph_x,0,-1,0,0,0,0,0,0)#y=-x+10
f5_name<-c("y=x+10")
glaph_y5<-PF00(glaph_x,10,-1,0,0,0,0,0,0)
#y=-x-10
f6_name<-c("y=x-10")
glaph_y6<-PF00(glaph_x,-10,-1,0,0,0,0,0,0)
#グラフ描画
plot(glaph_x,glaph_y1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(glaph_x,glaph_y2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_x,glaph_y3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_x,glaph_y4,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_x,glaph_y5,xlim=gs_x,ylim=gs_y,type="l",col=Cyan, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(glaph_x,glaph_y6,xlim=gs_x,ylim=gs_y,type="l",col=Yellow, main="",xlab="",ylab="")
#par(new=T)#上書き指定
#plot(f7,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")#基準線
abline(h=0)
abline(v=0)
#凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name,f4_name,f5_name,f6_name),lty=c(1,1,1,1,1,1),col=c(Red,Magenta,Blue,Green,Cyan,Yellow))#legend("bottomleft", legend=c(f1_name,f2_name,f3_name,f4_name,f5_name,f6_name),lty=c(1,1,1,1,1,1),col=c(Red,Magenta,Blue,Green,Cyan,Yellow))

以降は二項定理の世界に…
統計言語Rによる計算例
#a1=a2=a3=a4=a5=aN=0の時、a0
#そして微分1回目でa1*1=a1*1!=a1。右辺にXを置くとa1=x
D01<-expression(a1*x+a2*x^2+a3*x^3+a4*x^4+a5*x^5+aN^N)
D(D01,"x")
a1 + a2 * (2 * x) + a3 * (3 * x^2) + a4 * (4 * x^3) + a5 * (5 *
x^4)
#微分2回目でa2*2*1=a2*2!。右辺にx^2を置くとa2*2!=x^2→a2=x^2/2!
D01<-expression(a2*(2*x)+a3*(3*x^2)+a4*(4*x^3)+a5*(5*x^4)
)
D(D01,"x")
a2 * 2 + a3 * (3 * (2 * x)) + a4 * (4 * (3 * x^2)) + a5 * (5 *
(4 * x^3))#微分3回目でa3*3*2*1=a3*3!。右辺にx^3を置くとa3*3!=x^3→a3=x^3/3!
D01<-expression(a3*(3*(2*x))+a4*(4*(3*x^2))+a5*(5*(4*x^3))
)
D(D01,"x")
a3 * (3 * 2) + a4 * (4 * (3 * (2 * x))) + a5 * (5 * (4 * (3 *
x^2)))#微分4回目でa4*4*3*2*1=a4*4!。右辺にx^4を置くとa4*4!=x^4→a4=x^4/4!
D01<-expression(a4*(4*(3*(2*x)))+a5*(5*(4*(3*
x^2)))
)
D(D01,"x")
a4 * (4 * (3 * 2)) + a5 * (5 * (4 * (3 * (2 * x))))#微分5回目でa5*5*4*3*2*1=a5*5!。右辺にx^5を置くとa5*5!=x^5→a5=x^5/5!
D01<-expression(a5 * (5 * (4 * (3 * (2 * x))))
)
D(D01,"x")a5 * (5 * (4 * (3 * 2)))
#残りはaN*N!、すなわち剰余項はx^(n-1)/(n-1)!+x^n/n!
この応用で「オイラーの公式e^θi=Cos(θ)+Sin(θi)」が導出されたという次第。
ネイピア数を底(root)とする対数関数log(x)の求め方はトリッキーで、まず|x|<1の場合におけるlog(1+x)と-log(1-x)と両者の和log*1のマクローリン展開の結果を求めます。指数関数の「収束が遅い部分」だけ取り出した形ですね。
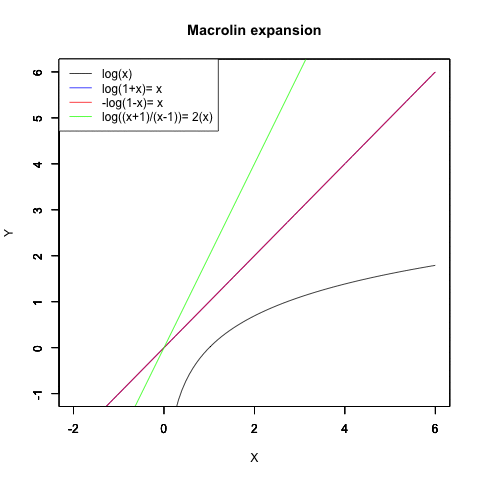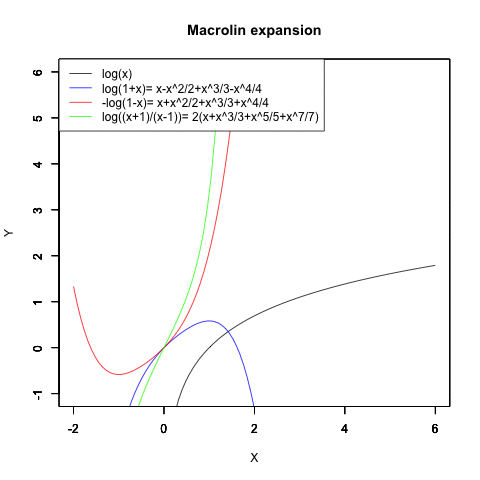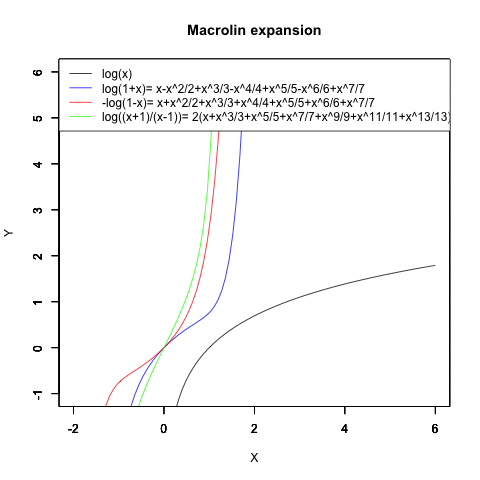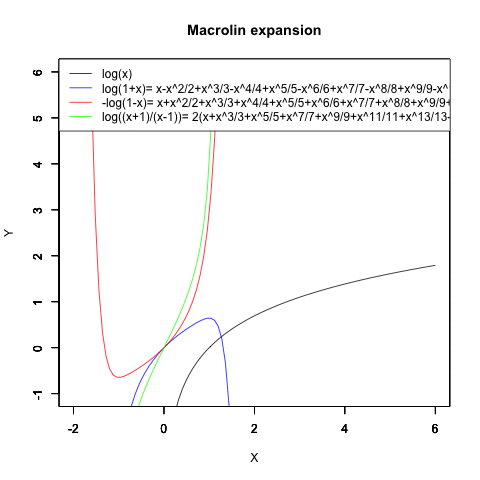

*1:1-x)/(1+x