ここでは指数(-n,-1,0,1,n)に対して(1/base^x,1/base^x,base/base,base,base^x)となるを返す指数関数y=底(root)^xや、逆に指数(-n,-1,0,1,n)を返す対数関数x=底(root)^yもしくはlog(x,base=底(root))を「現在」「過去」「未来」の3区間に分けて考えて見たいと思います。

#指数関数と対数関数の結果の対応
section01<-c("Past","Current","Current","Current","future")
exponential_result01<-c("root^-x","root^-1=1/root","root^0=root/root=1","root^1=root","root^x")
logarithm_result01<-c("log(1/root^x,base=root)=-x","log(1/root,base=root)=-1","log(1,base=root)=0","log(root,base=root)=1","log(root^x,base=root)=x")
Exponential_and_Logarithm01<-data.frame(Section=section01,Exponential_result=exponential_result01,Logarithm_result=logarithm_result01)
library(xtable)
print(xtable(Exponential_and_Logarithm01), type = "html")
| Section | Exponential_result | Logarithm_result | |
|---|---|---|---|
| 1 | Past | root^-x | log(1/root^x,base=root)=-x |
| 2 | Current | root^-1=1/root | log(1/root,base=root)=-1 |
| 3 | Current | root^0=root/root=1 | log(1,base=root)=0 |
| 4 | Current | root^1=root | log(root,base=root)=1 |
| 5 | future | root^x | log(root^x,base=root)=x |
①過去(Past)…指数関数の指数でいう-1未満の区間。
無視可能な状態(Ignorable State = 1/(root^x))の実例(IR)
#指数関数2^xあるいは対数関数log(x,base=2)の場合
target_numbers<-c("0.5=1/2","0.25=1/4","0.125=1/8","0.0625=1/16")
exponential_result<-c("2^-1=0.5","2^-2=0.25","2^-3=0.125","2^-4=0.0625")
logarithm_result<-c("log2(0.5)=-1","log2(0.25)=-2","log2(0.125)=-3","log2(0.0625)=-4")
Exponential_and_Logarithm<-data.frame(Target_numbers=target_numbers,Exponential_result=exponential_result,Logarithm_result=logarithm_result)
library(xtable)
print(xtable(Exponential_and_Logarithm), type = "html")
| Target_numbers | Exponential_result | Logarithm_result | |
|---|---|---|---|
| 1 | 0.5=1/2 | 2^-1=0.5 | log2(0.5)=-1 |
| 2 | 0.25=1/4 | 2^-2=0.25 | log2(0.25)=-2 |
| 3 | 0.125=1/8 | 2^-3=0.125 | log2(0.125)=-3 |
| 4 | 0.0625=1/16 | 2^-4=0.0625 | log2(0.0625)=-4 |
②未来(Future)…指数関数の指数でいう1以上の区間。
「 有意味な増大(Significant increase)」の実例(IS->SI)
#指数関数と対数関数の結果の対応
target_numbers<-c("4","8","16")
exponential_result<-c("2^2=4","2^3=8","2^4=16")
logarithm_result<-c("log2(4)=2","log2(8)=3","log2(16)=4")
Exponential_and_Logarithm<-data.frame(Target_numbers=target_numbers,Exponential_result=exponential_result,Logarithm_result=logarithm_result)
library(xtable)
print(xtable(Exponential_and_Logarithm), type = "html")
| Target_numbers | Exponential_result | Logarithm_result | |
|---|---|---|---|
| 1 | 4 | 2^2=4 | log2(4)=2 |
| 2 | 8 | 2^3=8 | log2(8)=3 |
| 3 | 16 | 2^4=16 | log2(16)=4 |
③現在(Current)…指数関数の指数でいう-1から+1にかけての区間。オイラーの等式e^iπ=-1やオイラーの公式e^iΘ=cos(Θ)+sin(Θi)などが切り抜いて単位円(半径1の円弧)に対応させる区間。

ここで底(root)の値を逆数化したり関数全体の符号を弄る形で指数関数a^xと対数関数Log(x,base=a)のイメージをさらに膨らましておきましょう。

①指数関数y=底(base)^x、対数関数x=底(root)^yもしくはlog(x,base=底(root))。底(root)の値はroot。
統計言語Rによる実際の計算例
#指数関数2^x
2^-1
[1] 0.5
2^0
[1] 1
2^1
[1] 2
#対数関数log(x,base=2)
log(1/2,base=2)
[1] -1
log(1,base=2)
[1] 0
log(2,base=2)
[1] 1
②底を逆転させた指数関数y=1/(底(base))^x、対数関数x=1/(底(root))^yもしくは-log(x,base=1/底(root))。指数との対応が逆転する。底(root)の値は1/root(root^-1)。
統計言語Rによる実際の計算例
#指数関数(1/2)^x
(1/2)^-1
[1] 2
(1/2)^0
[1] 1
(1/2)^1
[1] 0.5#対数関数log(x,base=1/2)
log(2,base=1/2)
[1] -1
log(1,base=1/2)
[1] 0
log(1/2,base=1/2)
[1] 1
③ここでいう①の式の符号を逆転させた指数関数y=-底(base)^x、対数関数x=-底(root)^yもしくはy=-log(x,base=底(root))。底(root)の値は-root。
統計言語Rによる実際の計算例
#指数関数-2^x
-2^-1
[1] -0.5
-2^0
[1] -1
-2^1
[1] -2
#対数関数-log(x,base=2)
log(1/2,base=2)
[1] -1
log(1,base=2)
[1] 0
log(2,base=2)
[1] 1
④ここでいう②の式の符号を逆転させた指数関数y=-1/(底(base))^x、対数関数x=-1/(底(root))^yもしくは-log(x,base=1/底(root))。底(root)の値は-1/root(-root^-1)。
統計言語Rによる実際の計算例
#指数関数(1/2)^x
-(1/2)^-1
[1] -2
-(1/2)^0
[1] -1
- (1/2)^1
[1] -0.5
#対数関数log(x,base=1/2)
-log(2,base=1/2)
[1] 1
-log(1,base=1/2)
[1] 0
-log(1/2,base=1/2)
[1] -1
全部合わせると以下の様になります。
- 例えば底(root)に2(2^1)もしくは1/2(2^-1)を取る指数関数・対数関数は全部で8個。
- 各曲線は単位円(半径1の円弧)上における0度(0ラジアン),90度(1/2πラジアン),180度(πラジアン)270度(3/2πラジアン)だけでなく、半径root^(-1/8)の円弧上の45度(1/4πラジアン),135度(3/4πラジアン),225度(5/4πラジアン),315度(7/4πラジアン)、半径root^(1/2)の円弧上の18度(π/10ラジアン),72度(1/2π-π/10ラジアン),108度(1/2π+π/10ラジアン),162度(π-π/10ラジアン),198度(π+π/10ラジアン),252度(3/4π-π/10ラジアン),288度(3/4π+π/10ラジアン),378度(2π-π/10ラジアン)で交差する。
- なんとなく全体に「無視可能な状態(IS=Ignorable State)」と「 有意味な増大(SI=Significant increase)」あるいは「有意味な減少(Significant Decrease = -(root^x))」の往復サイクルの様なものが見て取れる。
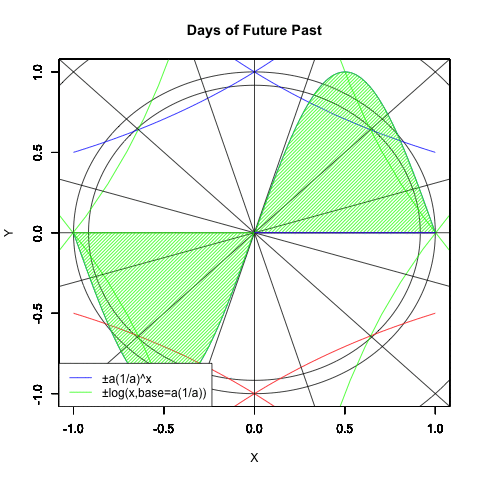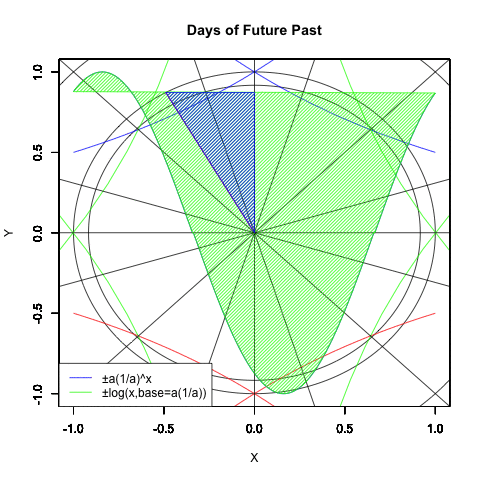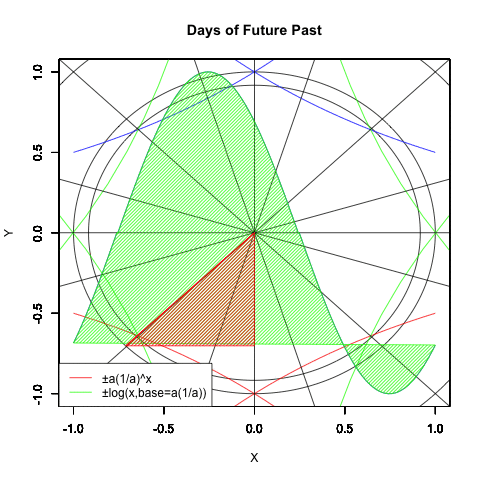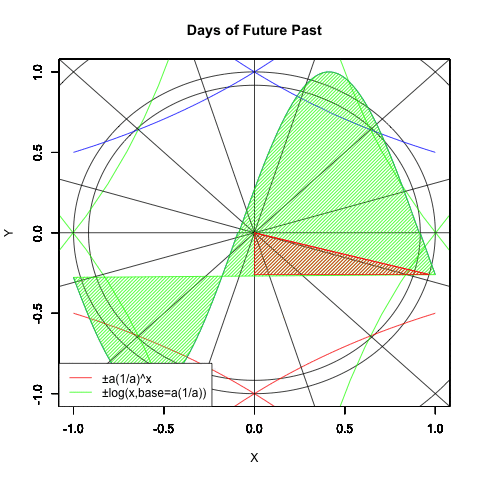
グラフに並べてみる。
#各指数関数・対数関数の交差点
Graph_scale_x<-c(-2,2)
Graph_scale_y<-c(-2,2)
theta <- seq(pi, -pi, length=360)
plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Days of Future Past", xlab="X", ylab="Y")par(new=T)#上書き指定
plot(cos(theta)* 2^(-1/8), sin(theta)* 2^(-1/8), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定par(new=T)#上書き指定
plot(cos(theta)*2/sqrt(2), sin(theta)*2/sqrt(2), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定
#指数関数
e0<-function(x){2^x}
plot(e0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e1<-function(x){1/2^x}
plot(e1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e2<-function(x){-1*(2^x)}
plot(e2,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e3<-function(x){-1*(1/2)^x}
plot(e3,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定#対数関数
tc <- seq(-6, 6, length=60) #-6から6までを60等分
l0<-function(x){2^x}
tcvals0 <- l0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定l1<-function(x){(1/2)^x}
tcvals1 <- l1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l2<-function(x){-1*(2^x)}
tcvals2 <- l2(tc) #それぞれの縦軸の値
plot(tcvals2,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l3<-function(x){-1**1
segments(-8,8,8,-8,col=rgb(0,0,0))
#18度(π/10)/72度の補助線
segments(-8,-(sin(pi/10))*8,8,(sin(pi/10))*8,col=rgb(0,0,0))
segments(-8,(sin(pi/10))*8,8,-1*(sin(pi/10))*8,col=rgb(0,0,0))
segments(-(sin(pi/10))*8,-8,(sin(pi/10))*8,8,col=rgb(0,0,0))
segments*2*8,-8,-1*(sin(pi/10))*8,8,col=rgb(0,0,0))
legend("bottomleft", legend=c("±a(1/a)^x","±log(x,base=a(1/a)))"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0)))

統計言語Rによる実際の計算例
#同心円2^(-1/8)2^(-1/8))
[1] 0.917004#同心円2^(1/2)
2/sqrt(2)
[1] 1.414214
2^0.5
[1] 1.414214
単位円(半径1の円弧)上における0度(0ラジアン),90度(1/2πラジアン),180度(πラジアン)270度(3/2πラジアン)の交差
#指数関数と対数関数の結果の対応
degrees_and_radians<-c("0Degrees(0Radians)","90Degrees(1/2πRadians)","180Degrees(πRadians)","270Degrees(3/2πRadians)")
fanctions01<-c("log(x,base=a)(IS) & log(x,base=1/a)(IS)","root^x(IS->SI) & 1/root^x(SR->IS)","-log(x,base=a)(IS) & -log(x,base=1/a)(IS)","-root^x(IS->SR) & -1/root^x(SI->IS)")
DRF01<-data.frame(Degrees_and_Radians=degrees_and_radians,Cross_Fanctions=fanctions01)
library(xtable)
print(xtable(DRF01), type = "html")
| Degrees_and_Radians | Cross_Fanctions | |
|---|---|---|
| 1 | 0Degrees(0Radians) | log(x,base=a)(IS) & log(x,base=1/a)(IS) |
| 2 | 90Degrees(1/2πRadians) | root^x(IS->SI) & 1/root^x(SR->IS) |
| 3 | 180Degrees(πRadians) | -log(x,base=a)(IS) & -log(x,base=1/a)(IS) |
| 4 | 270Degrees(3/2πRadians) | -root^x(IS->SR) & -1/root^x(SI->IS) |
半径root^(-1/8)の円弧上の45度(1/4πラジアン),135度(3/4πラジアン),225度(5/4πラジアン),315度(7/4πラジアン)の交差
#指数関数と対数関数の結果の対応
degrees_and_radians02<-c("45Degrees(1/4πRadians)","135Degrees(3/4πRadians)","225Degrees(5/4πRadians)","315Degrees(7/4πRadians)")
fanctions02<-c("1/root^x(SR->IS) & log(x,base=a)(IS)","root^x(IS->SI) & -log(x,base=a)(IS) ","-root^x(IS->SR) & -log(x,base=1/a)(IS) ","-1/root^x(SI->IS) & log(x,base=a)(IS)")
DRF02<-data.frame(Degrees_and_Radians=degrees_and_radians02,Cross_Fanctions=fanctions02)
library(xtable)
print(xtable(DRF02), type = "html")
| Degrees_and_Radians | Cross_Fanctions | |
|---|---|---|
| 1 | 45Degrees(1/4πRadians) | 1/root^x(SR->IS) & log(x,base=1/a)(IS) |
| 2 | 135Degrees(3/4πRadians) | root^x(IS->SI) & -log(x,base=a)(IS) |
| 3 | 225Degrees(5/4πRadians) | -root^x(IS->SR) & -log(x,base=1/a)(IS) |
| 4 | 315Degrees(7/4πRadians) | -1/root^x(SI->IS) & log(x,base=a)(IS) |
半径root^(1/2)の円弧上の18度(π/10ラジアン),72度(1/2π-π/10ラジアン),108度(1/2π+π/10ラジアン),162度(π-π/10ラジアン),198度(π+π/10ラジアン),252度(3/4π-π/10ラジアン),288度(3/4π+π/10ラジアン),378度(2π-π/10ラジアン)の交差
#指数関数と対数関数の結果の対応
degrees_and_radians03<-c("18Degrees(π/10Radians)","72Degrees(1/2π-π/10Radians)","108Degrees(1/2π-π/10Radians)","162Degrees(π-π/10Radians)","198Degrees(π+π/10Radians)","252Degrees(3/4π-π/10Radians)","288Degrees(3/4π+π/10Radians)","378Degrees(2π-π/10Radians)")
fanctions03<-c("1/root^x(SR->IS) & log(x,base=a)(IS)","root^x(IS->SI) & log(x,base=1/a)(IS)","1/root^x(SR->IS) & -log(x,base=1/a)(IS)","root^x(IS->SI) & -log(x,base=a)(IS)","-root^x(IS->SR) & -log(x,base=1/a)(IS)","-1/root^x(SI->IS) & -log(x,base=a)(IS)","-root^x(IS->SR) & log(x,base=a)(IS)","-1/root^x(SI->IS) & log(x,base=1/a)(IS)")
DRF03<-data.frame(Degrees_and_Radians=degrees_and_radians03,Cross_Fanctions=fanctions03)
library(xtable)
print(xtable(DRF03), type = "html")
| Degrees_and_Radians | Cross_Fanctions | |
|---|---|---|
| 1 | 18Degrees(π/10Radians) | 1/root^x(SR->IS) & log(x,base=a)(IS) |
| 2 | 72Degrees(1/2π-π/10Radians) | root^x(IS->SI) & log(x,base=1/a)(IS) |
| 3 | 108Degrees(1/2π-π/10Radians) | 1/root^x(SR->IS) & -log(x,base=1/a)(IS) |
| 4 | 162Degrees(π-π/10Radians) | root^x(IS->SI) & -log(x,base=a)(IS) |
| 5 | 198Degrees(π+π/10Radians) | -root^x(IS->SR) & -log(x,base=1/a)(IS) |
| 6 | 252Degrees(3/4π-π/10Radians) | -1/root^x(SI->IS) & -log(x,base=a)(IS) |
| 7 | 288Degrees(3/4π+π/10Radians) | -root^x(IS->SR) & log(x,base=a)(IS) |
| 8 | 378Degrees(2π-π/10Radians) | -1/root^x(SI->IS) & log(x,base=1/a)(IS) |
さらに底(root)を逆数化した関数と元関数はそれぞれの底(root)をスライドさせて連続化させる事が可能です。




①指数関数y=底(base)^xから指数関数y=1/(底(base))^xへの底(root)移動。指数0時点で傾きが消失しy=1となる。
#指数関数root^x
if01<-f0<-function(n){
f0<-function(x){2^x}
plot(f0,xlim=c(-5,5),ylim=c(0,5),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="2^x ~ (1/2)^x")
par(new=T)#上書き指定
f1<-function(x){1/2^x}
plot(f1,xlim=c(-5,5),ylim=c(0,5),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){n^x}
plot(f2,xlim=c(-5,5),ylim=c(0,5),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")abline(h=1)
abline(v=0)tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals <- f2(tc) #それぞれの縦軸の値polygon(c(-6,tc,6), #x
c(1,tcvals,1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色legend("topleft", legend=c("y=2^x","y=1/2^x","x=0,y=1"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if01(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

指数関数y=-底(base)^xから指数関数y=-1/(底(base))^xへの底(root)移動。指数0時点で傾きが消失しy=-1となる。
#指数関数-1*(root^x) ~ -1**3 #塗りつぶす色
legend("bottomright", legend=c("y=-(2^x)","y=-(1/2^x)","x=0,y=-1"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if01(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

対数関数x=底(root)^yもしくはlog(x,base=底(root))から対数関数x=1/(底(root))^yもしくはlog(x,base=1/底(root))への底(root)移動。指数0時点で傾きが消失しx=1となる。
#対数関数 log(x,base=root)
if02<-f0<-function(n){
f0<-function(x){log(x,base=2)}
plot(f0,xlim=c(0,5),ylim=c(-5,5),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="log(x,base=2~1/2)")
par(new=T)#上書き指定
f1<-function(x){log(x,base=1/2)}
plot(f1,xlim=c(0,5),ylim=c(-5,5),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){log(x,base=n)}
plot(f2,xlim=c(0,5),ylim=c(-5,5),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
abline(h=0)
abline(v=1)f3<-function(x){n^x}
tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals <- f3(tc) #それぞれの縦軸の値polygon(c(1,tcvals,1), #x
c(-6,tc,6), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
legend("topleft", legend=c("y=log(x,base=2)","y=log(x,base=1/2)","x=1,y=0"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if02(i)
}
}, interval = 0.1, movie.name = "TEST02.gif")

対数関数x=-底(root)^yもしくは-log(x,base=底(root))から対数関数x=-1/(底(root))^yもしくは-log(x,base=1/底(root))への底(root)移動。指数0時点で傾きが消失しx=1となる。
#対数関数 log(x,base=root)にマイナス符号をかけて反転
if02<-f0<-function(n){
tc <- seq(-6, 6, length=60) #-6から6までを60等分
f0<-function(x){-1*(2^x)}
tcvals0 <- f0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,xlim=c(-5,0),ylim=c(-5,5),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="log(x,base=2~1/2)")
par(new=T)#上書き指定
f1<-function(x){-1**4 #塗りつぶす色
legend("topleft", legend=c("y=-log(x,base=2)","y=-log(x,base=1/2)","x=-1,y=0"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if02(i)
}
}, interval = 0.1, movie.name = "TEST02.gif")

その基準円(半径1の円弧)上の振る舞いについては、三角関数に分類されているサイン関数sin(Θ)を彷彿とさせる側面も。
統計言語Rによる作表例
target_names<-c("0 radian & 0 degree","π/2 radian & 90 degree","π radian & 180 degree","3/2π& 270 degree","2π & 360 degree")
target_values<-c("0","1","0","-1","0")
Circular_function<-data.frame(Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Circular_function), type = "html")
| Target_names | Target_values | |
|---|---|---|
| 1 | 0 radian & 0 degree | 0 |
| 2 | π/2 radian & 90 degree | 1 |
| 3 | π radian & 180 degree | 0 |
| 4 | 3/2π& 270 degree | -1 |
| 5 | 2π & 360 degree | 0 |
統計言語Rでの実証例
#複素平面(球面)
Complex_plane<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_sin<-sin(theta01)
#方向の正負
ifelse*5#円弧の描写
plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Days of Future Past", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(cos(theta)* 2^(-1/8), sin(theta)* 2^(-1/8), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定
plot(cos(theta)*2/sqrt(2), sin(theta)*2/sqrt(2), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定
#指数関数
e0<-function(x){2^x}
plot(e0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e1<-function(x){1/2^x}
plot(e1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e2<-function(x){-1*(2^x)}
plot(e2,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
e3<-function(x){-1*(1/2)^x}
plot(e3,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
par(new=T)#上書き指定#対数関数
tc <- seq(-6, 6, length=60) #-6から6までを60等分
l0<-function(x){2^x}
tcvals0 <- l0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定l1<-function(x){(1/2)^x}
tcvals1 <- l1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l2<-function(x){-1*(2^x)}
tcvals2 <- l2(tc) #それぞれの縦軸の値
plot(tcvals2,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l3<-function(x){-1**6
segments(-8,8,8,-8,col=rgb(0,0,0))
#18度(π/10)/72度の補助線
segments(-8,-(sin(pi/10))*8,8,(sin(pi/10))*8,col=rgb(0,0,0))
segments(-8,(sin(pi/10))*8,8,-1*(sin(pi/10))*8,col=rgb(0,0,0))
segments(-(sin(pi/10))*8,-8,(sin(pi/10))*8,8,col=rgb(0,0,0))
segments*7*8,-8,-1*(sin(pi/10))*8,8,col=rgb(0,0,0))
#サイン波(ポリゴン)
polygon(theta00, #x
theta_sin, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色#インジケーター
segments(cos(dr[x]),sin(dr[x]),0,0,col=segC)
polygon(c(cos(dr[x]),0,0), #x
c(sin(dr[x]),sin(dr[x]),0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
#凡例
col=segC) #塗りつぶす色legend("bottomleft",legend=c("±a(1/a)^x","±log(x,base=a(1/a))"),lty=c(1,1),col=c(segC,rgb(0,1,0)))
}
#アニメーションさせてみる。library("animation")
#Time_Code=c(1,90,180,270)
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
一方、オイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θ)iの形となった時には、これまで見てきた様な「現在」「過去」「未来」の区分が消え、指数関数はX軸に沿って展開する周期関数Cos(θ)、対数関数はY軸に沿って展開する周期関数Sin(θ)そのものに変貌してしまいます。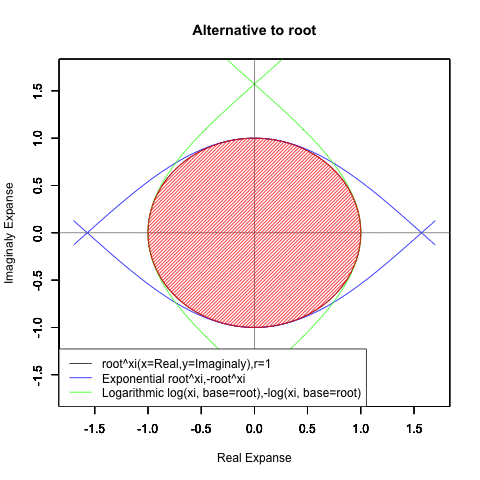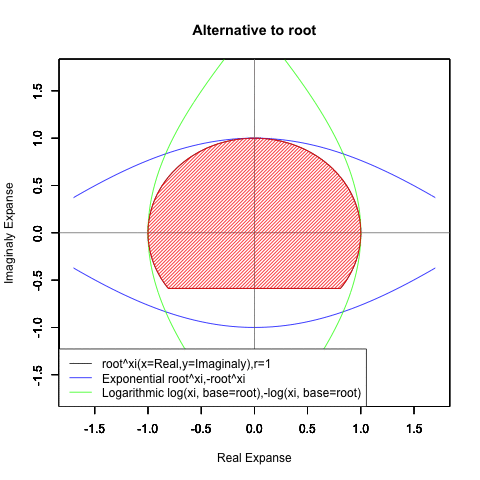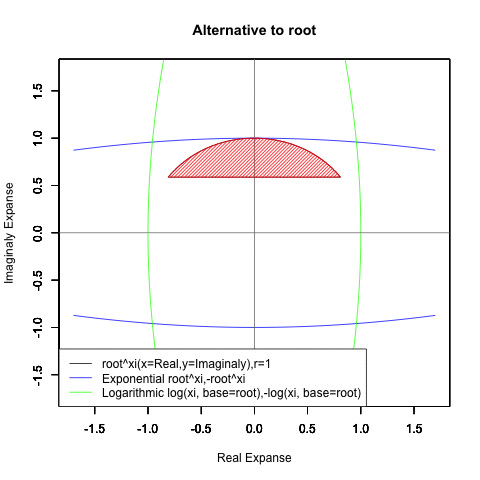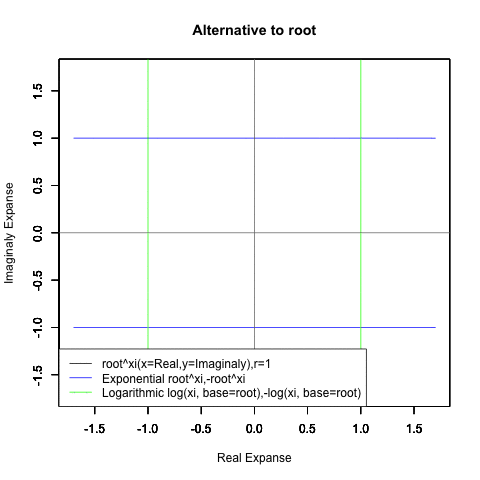
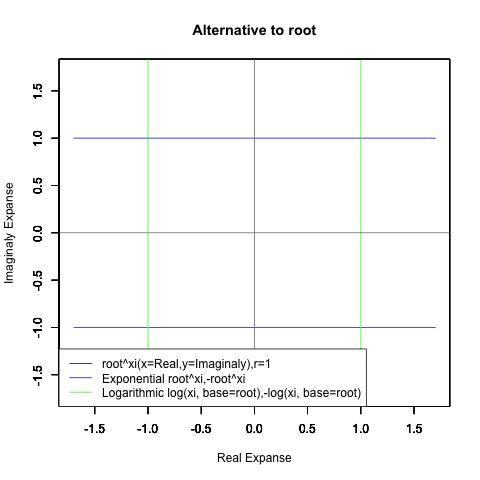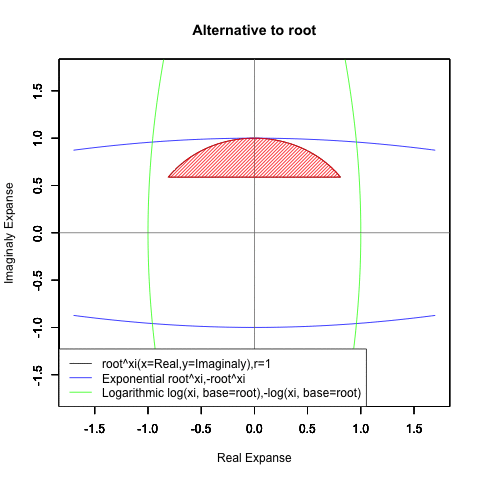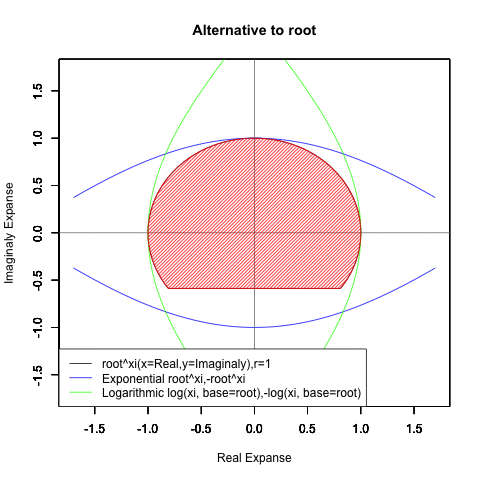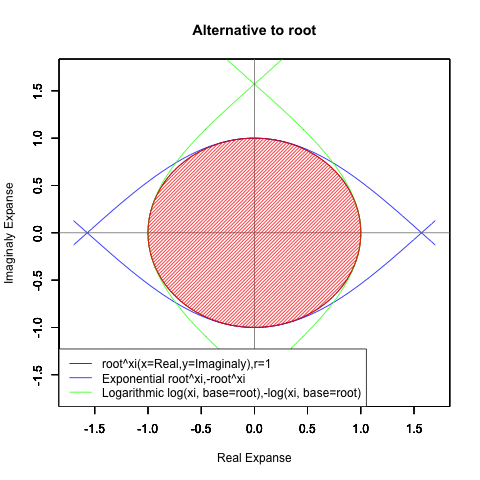
また「丁度1回だけ円を描く」のは底(root)がe(e^1,-e^1,log(1),-log(1))もしくは1/e(e^-1,-e^-1,log(1,base=1/e),-log(1,base=1/e))の場合だけで「現在」の区画では(円が完全に消えるe^0の区間を中心に)それが一部分しか描かれず「過去」「未来」の区画では逆にそれが幾重にも重ね書きされる展開を迎えます。
この変化を引き起こすのは「無限に奇関数と偶関数が連続する」指数関数や対数関数を「偶関数は実数軸に、奇関数は複素数軸に割り振ってそれぞれをCos関数とSin関数に変貌させてしまう」複素数Xiの働き。
要するに、ここでいう「指数関数a^xと対数関数Log(x,base=a)が本質的に内包する本質的に内包する特異な時間性(傾きなどは同じなのに「現在」を境界線に「過去」と「未来」が振る舞いを異にする)」のうち「現在」の部分だけを無造作に切り取って無限ループさせたのがオイラーの公式(Euler's formula)e^Xi=Cos(X)+Sin(Xi)で表される単位円(unit circle)の世界とも?
*1:1/2)^x)}
tcvals3 <- l3(tc) #それぞれの縦軸の値
plot(tcvals3,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
#90度(π/2)の補助線
abline(h=0)
abline(v=0)
#45度(π/4)の補助線
segments(-8,-8,8,8,col=rgb(0,0,0
*2:sin(pi/10
*3:1/root)^x)にマイナス符号をかけて反転
if01<-f0<-function(n){
f0<-function(x){-1*(2^x)}
plot(f0,xlim=c(-5,5),ylim=c(-5,0),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="2^x ~ (1/2)^x")
par(new=T)#上書き指定
f1<-function(x){-1*(1/2)^x}
plot(f1,xlim=c(-5,5),ylim=c(-5,0),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){-1*(n^x)}
plot(f2,xlim=c(-5,5),ylim=c(-5,0),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
abline(h=-1)
abline(v=0)
tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals <- f2(tc) #それぞれの縦軸の値
polygon(c(-6,tc,6), #x
c(-1,tcvals,-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0
*4:1/2)^x)}
tcvals1 <- f1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,xlim=c(-5,0),ylim=c(-5,5),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){-1*log(x,base=n)}
plot(f2,xlim=c(-5,0),ylim=c(-5,5),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
abline(h=0)
abline(v=-1)
f3<-function(x){-1*(n^x)}
tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals3 <- f3(tc) #それぞれの縦軸の値
polygon(c(-1,tcvals3,-1), #x
c(-6,tc,6), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0
*5:x>180),segC<-rgb(1,0,0),segC<-rgb(0,0,1
*6:1/2)^x)}
tcvals3 <- l3(tc) #それぞれの縦軸の値
plot(tcvals3,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
#サイン波
plot(theta00,theta_sin,xlim=Graph_scale_x, Graph_scale_y, type="l",col=rgb(0,0,1),,main="",xlab="", ylab="")
#90度(π/2)の補助線
abline(h=0)
abline(v=0)
#45度(π/4)の補助線
segments(-8,-8,8,8,col=rgb(0,0,0
*7:sin(pi/10