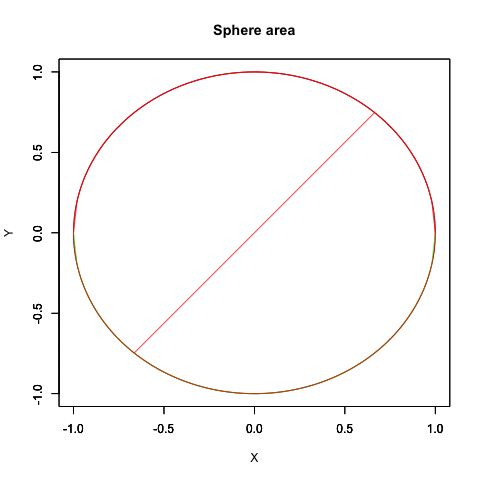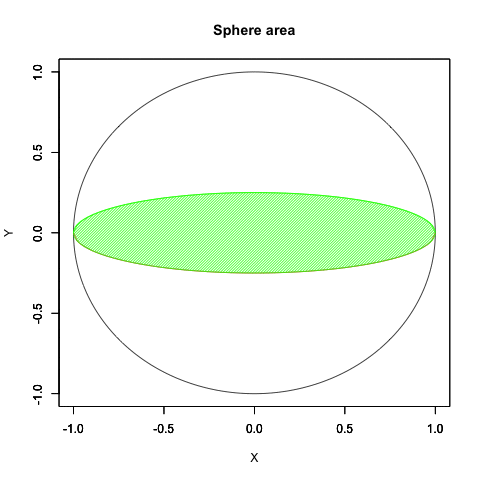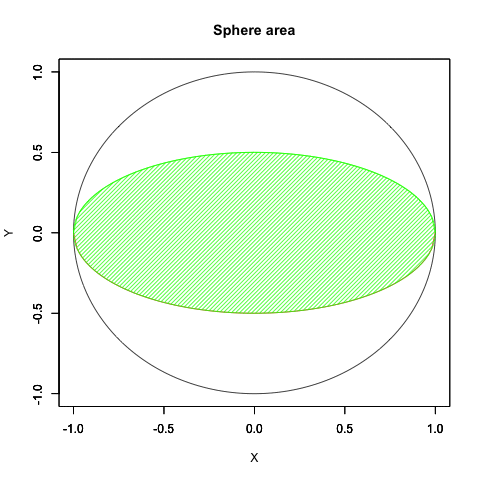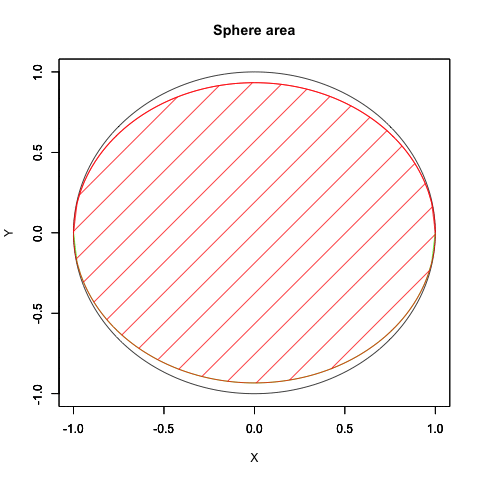
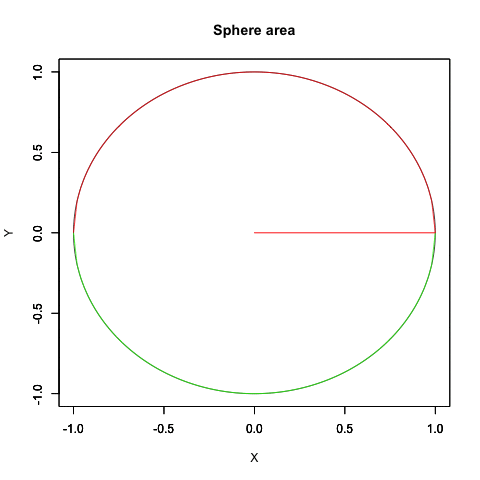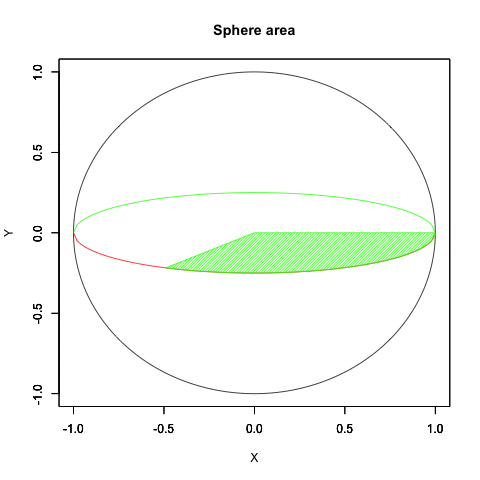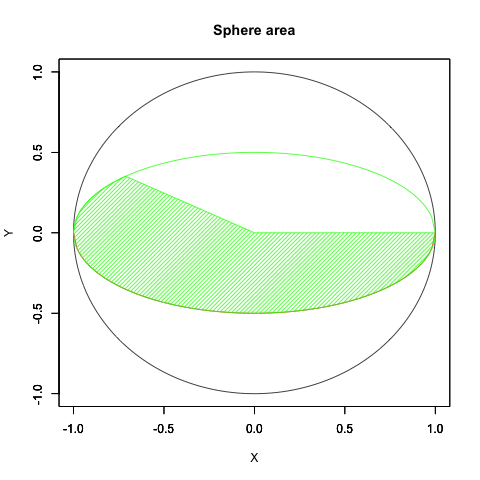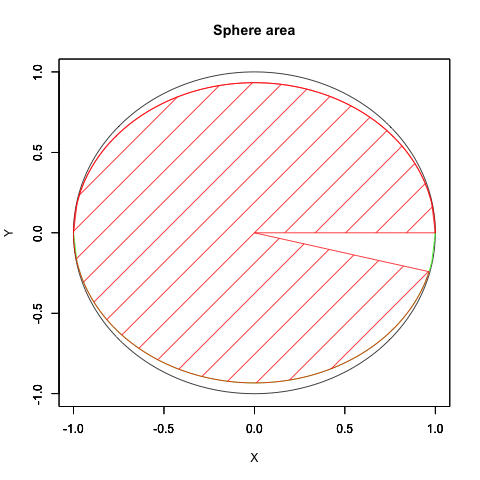
要するに円弧はプロッティング上、絶対値を同じくする周期関数2つを90度位相をズラしてx軸とy軸に割り振ると描かれるのです。
なので「-πからπにかけて値をX軸のCos関数とY軸のSin関数に与える」と考えても結果は同じとなり、しかもこの場合にはネイピア数eや複素数を登場させず済みます。
統計言語Rによる実演例「最もシンプルな円の描き方」
theta <- seq(pi, -pi, length=360)
plot(cos(theta), sin(theta),xlim=c(-1,1),ylim=c(-1,1), type="l",col=rgb(0,1,0), main="Simple Circle Draw", xlab="cos(x)", ylab="sin(x)")

これ実は「物理屋の発想」で、数学におけるそれとは導出過程が全く異なります。
大きさを持たない点または大きさを持つ物体が、ある点を中心としてあるいは直線を軸として、あるいは別の物体の周りを回る運動。この点を回転中心、この直線を回転軸という。
- 回転中心や回転軸が回転する物体の内部にある場合を特に自転というときもある。
- まさに運動している状態を指す場合も、運動の始状態から終状態への変化や移動を指す場合もある。前者の意味を強調したい場合は回転運動ということもある。
転じて、資金などの供給・サービス業の客の出入りなどをこう称する場合がある。
点の回転と等速円運動
物理的または数学的な文脈での回転とは、特に断らなくとも、回転中心や回転軸から回転する点への距離が一定の運動、つまり円運動を指すことが多い。また、回転した点の軌跡が円の一部である円弧(扇形の曲線部)の場合を指すことも多い。
- これらの円や扇形の半径を回転半径(Turning radius)という。
- 回転の軌跡である円弧の中心角、すなわち、回転中心から回転する点の始めにおける位置へ引いた直線と、終わりにおける位置へ引いた直線とのなす角を回転角(Angle of rotation)という。
- 単位時間当たりの回転角を、その回転運動の角速度(angular velocity)という。
回転半径と角速度が一定な回転運動を等速円運動という。特に断らなくとも、回転という言葉が等速円運動の意味に限定されていることも多い。
そう、物理学の次元では「まず等速円運動ありき」で話が始まるのです。
統計言語Rによる3D表示(z軸=t)
library(rgl)
complex_plane_z<-seq(-3*pi,3*pi,length=180)
complex_plane_x<-cos(complex_plane_z)
complex_plane_y<-sin(complex_plane_z)
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")


回転の向き
ひとつの平面内の等速円運動の回転の向きは2通りが可能であり、どちらかの向きの回転の角速度を正と定め他方を負と定めれば、可能な全ての回転(等速円運動)を正負の実数で定めた角速度、および正の実数値をとる回転半径の長さ、および回転中心の位置で指定できる。
3次元空間内ではさらに回転(等速円運動)の軌跡を含む平面を指定しなくてはならない。
- この平面を回転面または回転平面という。
- 3次元空間内の回転の角速度は、回転平面に垂直で平面内で定義した角速度の大きさに比例する大きさを持つベクトル量として表すことができる。このベクトルの向きは2通りが可能だが、通常の定義では、右ネジを回転方向に回した時にネジが進む方向を角速度ベクトルの向きとする。
*いわゆる「右手系」とはこれ。
こうして3次元空間内での可能な全ての回転(等速円運動)は、3次元ベクトルとして定義した角速度と回転半径と回転中心の位置で指定できる。
回転半径(Turning radius)
観測対象の座標を観測原点からの距離と角度で表す極座標系(polar coordinates system)などにおいて観測原点と観測対象を結ぶ半直線の距離rを指す。
- 数学史上、こうした定義は最初1811年頃にガウスによって導入された(ただしそれに先立つ1806年に Jean-Robert Argandも同様の手法を用いていおり、さらには1797年の Caspar Wesselの書簡でも同様の概念が語られている)数平面(独Zahlenebene)/複素数平面(独Komplexe Zahlenebene, 英complex plane)/ガウス平面 (Gaussian plane) /アルガン図 (Argand Diagram)の概念上において実数直線 (real line) を実軸 (real axis) として平面の直交座標 (x, y) のx軸に配置し、Y軸をy-軸を純虚数の全体に対応する虚軸 (imaginary axis) と配置するアイディアとして現れた。xy-平面上の点 (x, y) に複素数z = x + iyを対応させるのでz-平面とも言う。
統計言語RにおけるXY座標から極座標への変換
complex(mod=c(1,2), arg=c(0, pi)) # mod:絶対値,arg:偏角
[1] 1+0.000000e+00i -2+2.449213e-16iz<-complex(real=3,imaginary=2)
print(z)
[1] 3+2i
Re(z) # 実数成分を取り出す
[1] 3
Im(z) #虚数成分を取り出す
[1] 2
Conj(z) # 共益複素数
[1] 3-2i
#極座標(polar coordinates)表示関係
Mod(z)
[1] 3.605551
sqrt(Re(z)^2+Im(z)^2)
[1] 3.605551
# 複素平面ではz=x+ iy として「絶対値(Mod)=距離」sqrt(x^2+y^2)=Mod(z)
Arg(z)
[1] 0.5880026
#z=x+iy = Mod(z) * cos(t)+i sin(t); t=Arg(z)
Mod(z)*(cos(Arg(z))+complex(real=0,imaginary=1)*sin(Arg(z))
[1] 0.5880026
#汎用代数言語Yacasをライブラリ化したRYacasにおける極形式の扱い。
library(Ryacas)
yacas("Mod(1+I)") #絶対値
expression(remainder(complex_cartesian(1, 1)))
yacas("Arg(1+I)") #偏角
expression(pi/4)- やがてこうした概念をハミルトン (Sir William Rowan
Hamilton, 1805〜1865) が3次元へと応用する形で四元数(quaternion) を発明。ただし、あまりに複雑すぎる為にこれを簡略化したベクトルや線形代数の概念が数学や物理学の世界に広まっていく。
ベクトル・テンソル解析
これマジで面白すぎる。自分は最初にベクトル解析を習った身なので、四元数については「なんか変なトリックを使って無理やり外積と内積をまとめたやつ」みたいに見えるけど、先に四元数を習うと「積が二種類あるのはキモすぎる」になるんやろなぁ https://t.co/L1wuEAVOde
— 解答略 (@kaitou_ryaku) April 27, 2019
複素数の掛け算を行うと、(aーib)(c+id)=(ac+bd)+i(adーbd)と2次元ベクトルの内積と外積が現れる。3次元ベクトルで同じことをやりたかったら、四元数を使う。
— 新函館北斗の女♪(緒方秀教カラオケは適度に嗜む) (@HideOgata) December 9, 2017
習う順番は、普通、
— 中嶋慧 (@subarusatosi) December 2, 2017
ベクトル解析 → 四元数 → 微分形式
だけど、発見の順番は、
微分形式 → 四元数 → ベクトル解析。
微分形式の芽生え:1844年(グラスマン)
[外積はあるが、外微分はない?]
テンソル解析:1901年(リッチ, レビ・チビタ)
ベクトル解析:1900年ごろ(ヘヴィサイド, ギブス)
ちなみにハミルトンの四元数概念はその後、宇宙船やドローンの飛行、3Dポリゴンゲームの世界において再評価される展開を迎える。
回転角(Angle of rotation)
一般角(General angle)を決めれば動径(Radius、角を半直線の回転で定義するとき、もとの半直線(Front line、始線)に対して回転したと考えられる方の半直線)が定まるが(両者の関係が1:多なので)動径を決めても角度は1つには定まらない。
- 一般角(General angle)…弧度法(circular measure)に従って弧長lと半径rの中心角θをθ=lrと定義した尺度。例えば半径r=1の時、弧長l=360度と置けば中心角θは360度で一周する値、弧長l=2πと置けば2πで一周する値によって表示される事になる。
- 動径(Radius)…極座標系(polar coordinates system)などにおいて角を(観測原点から観測対象の間に仮に引かれた)半直線の回転で定義するとき、始線(Front line)に対して回転したと考えられる方の半直線
例えば始線OXから「+30°回ったとき」「-330°回ったとき」「+390°回ったとき」いずれも動径OPに一致する.
角速度(angular velocity) - Wikipedia
運動学においてある点をまわる回転運動の速度を、単位時間に進む角度によって表わした物理量である。言い換えれば原点と物体を結ぶ線分、すなわち動径が向く角度の時間変化量である。
- 円運動する物体に対する角速度ベクトル Ω と位置ベクトル r、速度ベクトル v の関係。それぞれのベクトルは(後述する右手の法則に従って)互いに直交している。
特に等速円運動する物体の角速度は、物体の速度を円の半径で割ったものとして与えられる。従って角速度の量の次元は、通常の並進運動の速度とは異なり時間の逆数 T^-1(1/T)となる。
- 角速度はある座標系における動径(角を半直線の回転で定義するとき、もとの半直線(始線)に対して回転したと考えられる方の半直線)の角度の時間微分であるが、角速度の時間微分は角加速度と呼ばれ、ある時刻間における回転角を与える。
- また、角速度の絶対値(またはノルム)をしばしば角速度の大きさと呼ぶが、文脈によっては、角速度の大きさを含めて単に「角速度」と呼ぶこともある。
その単位は角度の単位と時間の単位の比によって表わされる。例えば国際単位系においては、角度の単位はラジアン (rad)、時間の単位は秒 (s) であるため、角速度の単位はラジアン毎秒 (rad/s) となる。角速度を表す記号としてはしばしばギリシア文字の ω や Ω が用いられる。
自由振動(free oscillation/free vibration) - Wikipedia
ある系がその固有振動数で振動することである。減衰のない自由振動では強制振動とは異なり、系に外部から力が作用しなくても運動し続ける。
フックの法則(Hooke's law)F=-kx
多くの弾性体では変形の量が小さい限り復元力Fと変形量kxの間にF=-kx の比例関係がある。ここでxは自然長からの伸びまたは縮み(自然長とは、荷重のないばねが自然に停止する位置)、Fはばねによる反力、kはばね定数と呼ばれる個々のばねの固有値(ばねの強さ)。
これをその発見者である17世紀のイギリスの物理学者ロバート・フックの名にちなんでフックの法則とよぶ。
- フックは1676年にラテン語のアナグラムでこの法則を記述し、1678年にアナグラムの答えが羅: Ut tensio, sic vis (英: As extension, so is force)、即ち「 伸びとともに、力あり(力は伸びに比例する)。 」であると発表した。
「ばねの伸びと弾性限度以下の荷重は正比例する」なる近似的法則で弾性の法則とも呼ばれる。板や棒の曲げのような、伸び縮みとは別種の変形でも同じように成り立つ。
単振動(Simple harmonic motion)または調和振動(harmonic motion)
等速円運動の正射影の運動と同一である。等速円運動に光を当てると影ができる。この影の運動が単振動なのである。
- 単振動している物体を調和振動子(Harmonic oscillator)と呼ぶ。
単振動は等速円運動の正射影であるために、その性質が等速円運動と非常によく似ている。ちなみに単振動では回転数のことを振動数という。定義は回転数と同じ。
時刻0のときの物体の位置xは運動式C*sin(ω*t+φ)に従う正弦波を描くが、そこで各数値はそれぞれ以下のような物理量となる。
時刻0のときの物体の位置x=C*sin(ω*t+φ)
C…振幅=物体の最大の変位の絶対値
ω…角振動数(固有振動数)
t…指定時刻
φ…初期位相統計言語Rによるグラフ化例
plot(sin,xlim=c(-8,8),ylim=c(-1,1),main="Simple harmonic motion",xlab="t",ylab="C*sin(ω*t+φ)")
すなわち「等速円運動のX軸への写像(Cos波)をX軸に、等速円運動のY軸への写像(Sin波)をY軸に配置すると当然の如くX-Y軸上における等速円運動が再現される」という事。
改めて元グラフに目をやってみましょう。確かに「等速円運動のX軸への写像(Cos波)をX軸に、等速円運動のY軸への写像(Sin波)をY軸に配置した等速円運動の再現図」になってます。物理学的定義ではX軸上の写像Cos波、Y軸の写像それぞれが調和振動子(Harmonic oscillator)となり、それを同期させているe^Xi関数は、クォーツ時計の針を動かしている水晶振動子(Xtal=quartz crystal unit/crystal unit)同様にカプセル化(ブラックボックス化)されてしまうという次第。



水晶振動子(Xtal=quartz crystal unit/crystal unit) - Wikipedia
水晶(石英)の圧電効果を利用して高い周波数精度の発振を起こす際に用いられる受動素子の一つ。水晶発振子と呼ばれることもある。クォーツ時計、無線通信、コンピュータなど、現代のエレクトロニクスには欠かせない部品となっている。
原理
圧電体である水晶の結晶に電圧を加える(電界を印加する)と、圧電体に変形が生ずる。この現象の発見者は、ジャックとピエール・キュリーの兄弟である。
ピエール・キュリー(Pierre Curie, 1859年〜1906年) - Wikipedia
フランスのパリ生まれ。通学を嫌い、14歳まで医者である父ウジューヌ・キュリーや家庭教師、兄ジャックらから教育を受けたが、やがて数学と幾何学に大きな才能を示し始めた。16歳でパリ大学(ソルボンヌ)に入学し、18歳で学士号を取得し卒業したが、貧乏だったため博士課程にすぐには進めず、物理研究室の助手として働き始めた。
結晶と磁性の研究
1880年、同じくパリ大学鉱物学助手の兄ジャックと共に水晶などの結晶に圧力をかけると電位が発生するという圧電効果(ピエゾ効果)を発見、公表。翌年の1881年には逆の現象、すなわち水晶に電界を印加すると微妙に変形するという現象を確認した。今日、この現象を応用した水晶振動子が多くのデジタル回路で使われている。
磁性に関する有名な博士論文の前に、自差係数を計測するための精密なねじりばかりを設計し完成させた。この装置の原理は精密な計測を必要とするその後の研究者に広く使われた。
また博士論文のテーマとして強磁性、常磁性、反磁性について研究して常磁性への温度の影響を発見し、いわゆる「キュリーの法則」として定式化した。その式に出てくる物質固有の定数は「キュリー定数」と呼ばれている。また強磁性体が温度を上げるとその性質を失うことを発見した。この業績にちなみ、鉄などの強磁性体がその磁性を失う温度のことを「キュリー温度(キュリー点、Curie Temperature)」という。また、高感度の科学天秤も製作し、これはキュリー天秤と呼ばれる。
また今日では「キュリーの原理」として知られている原理を定式化した。すなわち物理現象において、原因に非対称性がないかぎり、結果にも非対称性は現れないという原理である。例えば、無重力状態で無作為に混ぜた砂には非対称性がない(等方性である)。そこに重力場を導入すると、重力の方向によって非対称性が現れる。すると、砂は重力方向に深くなるほど密度が高くなり、重力場の非対称性を反映した状態となる。
このような成果を挙げながら、ピエールは1883年から就いたパリ市立工業物理化学高等専門大学 (EPCI) の教職で得る薄給のまま研究に没頭する日々を送った。出世に興味を持たず、教育功労勲章も断っていた。ただし外国では既に高い評価を得ており、1893年にはイギリスのウィリアム・トムソン(ケルヴィン卿)が訪問し、科学について話し合っている。
*有名な放射性元素の研究で名を馳せるのは1894年春にポーランド没落貴族の娘マリア(仏語名マリ)・スクウォドフスカと出逢い、熱烈なプロポーズの末1895年7月26日に結婚して以降。その後二人は共同で放射性物質の研究を行い、ポロニウムとラジウムを発見。"radioactivity"(放射能)なる用語を作ってその先駆的研究を行ったが、そこではピエールと兄のジャックが製作した高感度な圧電式電位計が重要な役割を果たしている。ラジウム粒子が継続的に熱を放射していることを発見し、核エネルギーの発見者となったのもまたピエールと学生の1人だった。彼はまた磁場を使って放射性物質の放射の特性を調べ、一部の放射が正に帯電し、一部は負に帯電し、一部は帯電していないことを示した。これらはアルファ線、ベータ線、ガンマ線に対応している。電気的特性としては、通常はコンデンサとして作用するが、その固有振動数に近いある特定の周波数帯でのみコイルのように誘導性リアクタンスをもつものとして動作する。この原理を応用した電子部品が水晶振動子である。一般的な水晶振動子であるAT振動子は圧電体である水晶片(水晶ブランク)を2枚の電極で挟んだ水晶振動体を保持器に収めたものである。水晶振動子は自由振動を起こすため、波形は正弦波となる。
周波数
発振回路において、トランジスタとコイル・コンデンサの接続の組み合わせにより発振の条件が決まる回路がある(ハートレー発振回路、コルピッツ発振回路など)。これらの回路のうち、コイルが発振の条件として必要な部分に水晶振動子を接続すると、その固有振動数の発振出力が得られる。その周波数は106オーダーの精度が容易に得られ、他に類を見ないものであることから、周波数や時間の基準として広く用いられている。
結晶の大きさの関係から、実用に用いられている水晶振動子は1 - 20MHz程度のものが多い。それ以上の周波数が必要なときは、オーバートーン発振させるか(あるいは高い周波数用の水晶振動子は、オーバートーンで使用する前提のものもある)、周波数逓倍器を用いる。
水晶振動子の発振周波数自体は、水晶振動子の特性によって決まるため、基本的には変更できない。そのため無線通信などでは、用いる周波数に合わせて水晶振動子を差し替える方式が採られることもある。しかしながら、外部のキャパシタンスを調整することによって、±0.数%程度の微調整が可能であり、これを応用したVXO (Variable Xtal Oscillator)、キャパシタンスを可変容量ダイオードに置換して電圧制御できるようにしたVCXO(Voltage Controlled Xtal Oscillator、電圧制御水晶発振器)等の回路がある。また、水晶振動子と電圧制御発振器、デジタル回路によるカウンタ回路や位相比較器等を組み合わせた周波数シンセサイザによって、安定した任意の周波数の出力信号を得ることも可能である。
ある意味完全な循環論法とも見て取れますが…物理屋の発想では「結果良ければ全て良し」?