【多角形方程式情報倉庫】「ジンバルロック問題」とは何か① - 「諸概念の迷宮（Things got frantic）」用語集

f:id:ochimusha01:20191011182957j:plain

とりあえず現在取り掛かってるプログラムが以下。

これまで積み上げてきた右手法に基づく座標体系では「X軸＝前後」「Y軸＝上下」となるので自然な拡張として「Z軸=左右」となる。
画面上では重ねて表示する事しか出来ないので、航空機のナビゲーション・ライトの規定に従って「右=緑」「左=赤」なる表示方法を採用する。

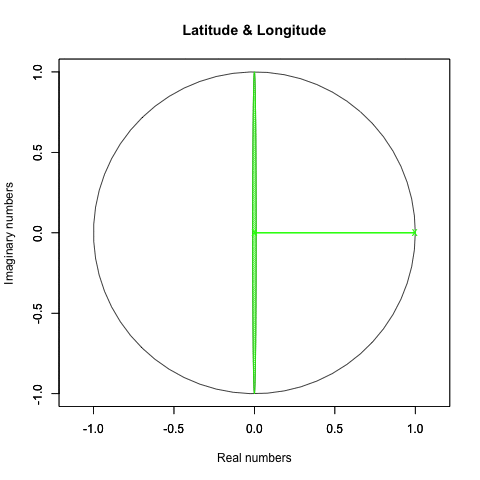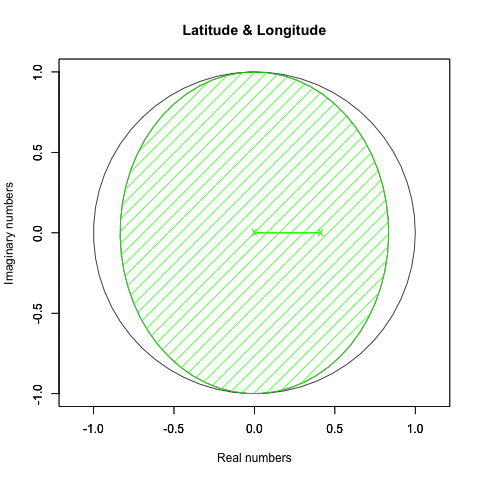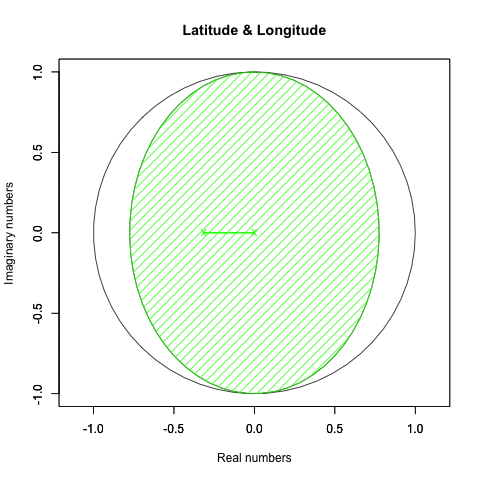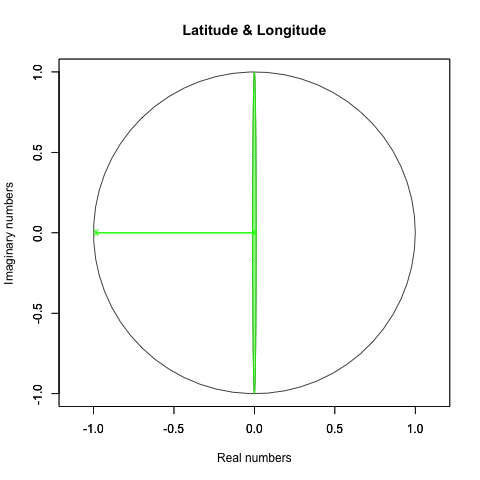
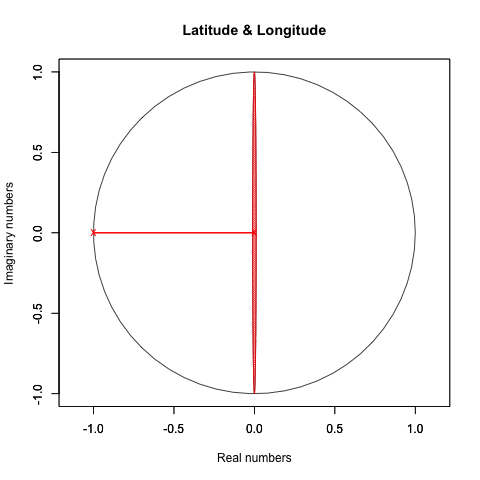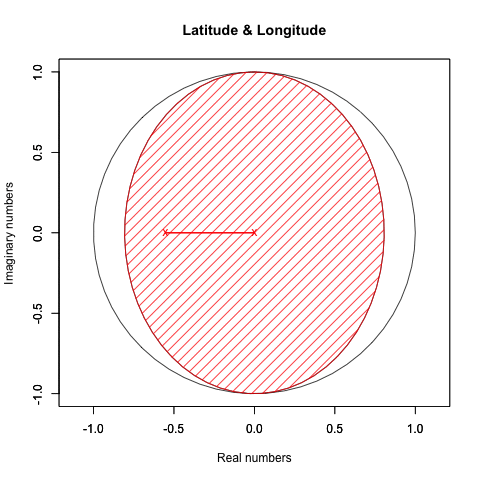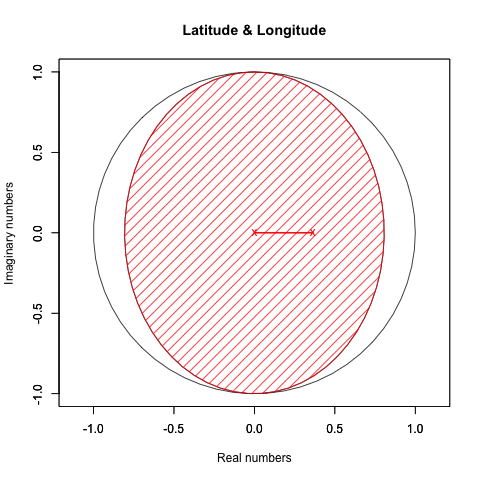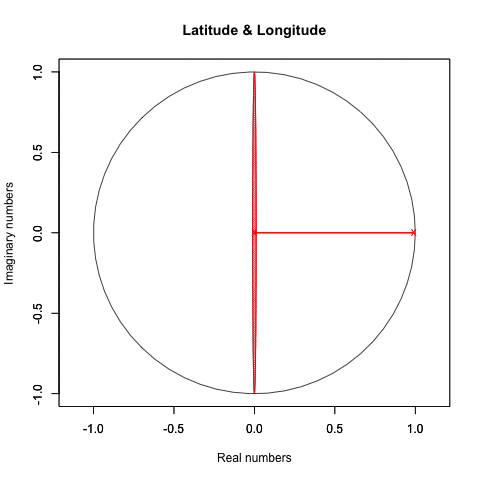
統計言語Rによる作画例（緯度と経度の回転）

#複素平面（球面）
Circle_Divide<-60 #円分割数
Complex_plane01<-function(x){

#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- seq(0,2*pi,length=Circle_Divide)
cercle01<-exp(theta*(0+1i))
crcl_r<-Re(cercle01)
crcl_i<-Im(cercle01)

#XY軸沿いの回転
xy_radian<-Re(x)
XY_Rotation_ratio<-cos(2*xy_radian/Circle_Divide*2*pi)/2+0.5
XYR_cos=crcl_r
XYR_sin=crcl_i*XY_Rotation_ratio

#塗り潰し色（「右」が緑、「左」が赤）
ifelse*1
#Z軸沿いの回転
z_radian<-Im(x)
Z_Rotation_ratio<-z_radian/Circle_Divide*pi*2
XYZ_Rotation<-complex(real=XYR_cos,imaginary=XYR_sin)*(cos(Z_Rotation_ratio)+sin(Z_Rotation_ratio)*(0+1i))
XYZ_Rotation_cos<-Re(XYZ_Rotation)
XYZ_Rotation_sin<-Im(XYZ_Rotation)

#Z軸沿いの回転（インジケーター）

ing<-complex(real=0,imaginary=crcl_i[xy_radian])*(cos(Z_Rotation_ratio)+sin(Z_Rotation_ratio)*(0+1i))

Ing_r<-Re(ing)
Ing_i<-Im(ing)

#円弧描写
plot(crcl_r, crcl_i,asp=1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Latitude & Longitude", xlab="Real numbers", ylab="Imaginary numbers")
par(new=T)#上書き指定

#円弧の描写（回転）
plot(XYZ_Rotation_cos,XYZ_Rotation_sin,asp=1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",main="", xlab="", ylab="")
segments(Ing_r,Ing_i,0,0,col=LR_color,lwd=2)
text(Ing_r,Ing_i,"x",col=LR_color)
text(0,0,"x",col=LR_color)
#円の塗り潰し
polygon(XYZ_Rotation_cos, #x
XYZ_Rotation_sin, #y
density=c(50*(1-XY_Rotation_ratio)), #塗りつぶす濃度
angle=c(45),　　　　#塗りつぶす斜線の角度
col=LR_color) 　#塗りつぶす色
}

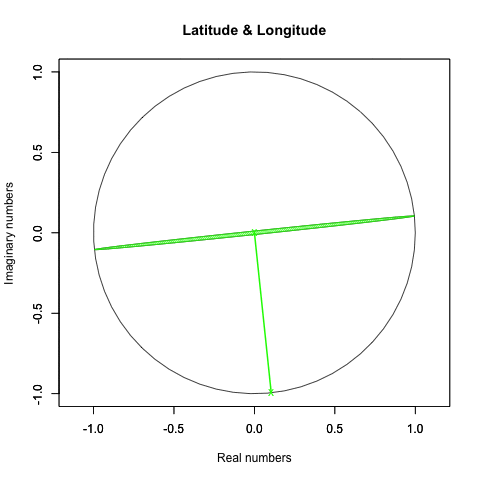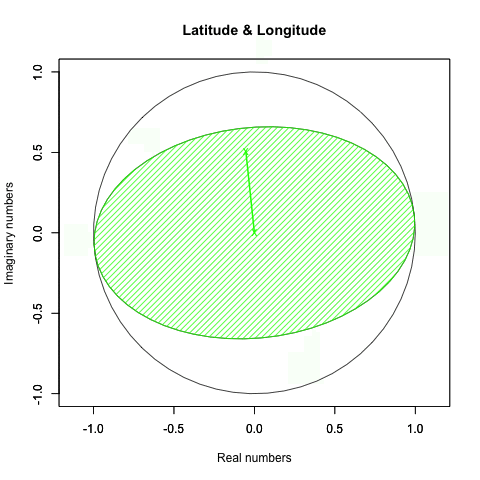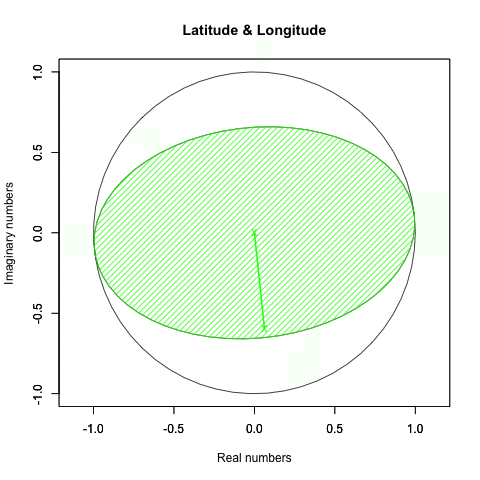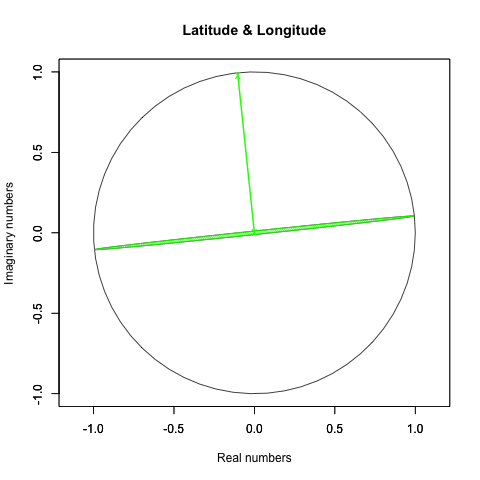
X軸のみ回す（Y軸とZ軸は0固定）とこう見えます。

library("animation")
#アニメーションさせてみる。
TC00=seq(0,2*pi,length=Circle_Divide/2)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]
Time_Code<-complex(re=TC02, im=rep(1,length=Circle_Divide/2))
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo01.gif")

f:id:ochimusha01:20191011021040g:plain
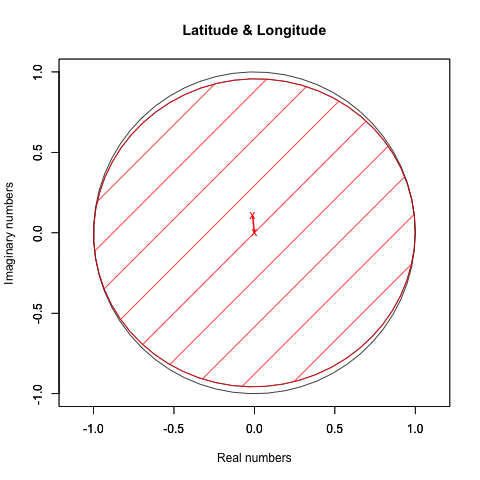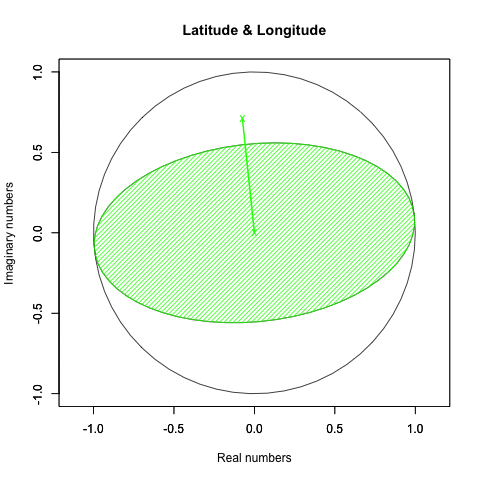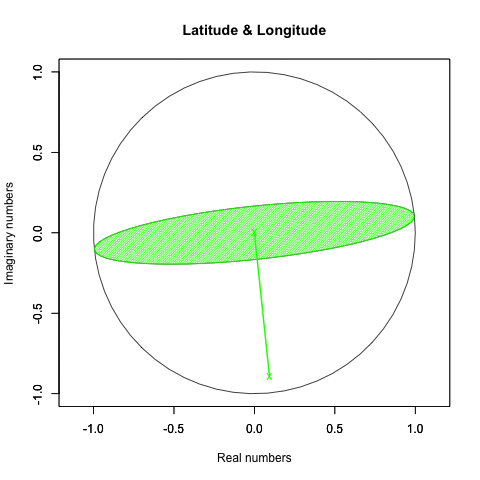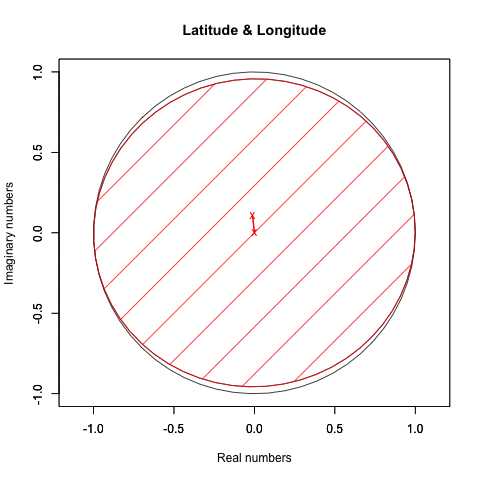
Y軸のみ回す（Y軸はπ/4固定、Z軸は0固定）とこう見えます。

library("animation")
#アニメーションさせてみる。
TC00=seq(0,2*pi,length=Circle_Divide/2)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]
Time_Code<-complex(re=TC02, im=rep(Circle_Divide/4,length=Circle_Divide/2))
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo02.gif")

f:id:ochimusha01:20191011160920g:plain

一方、X軸が45度（1/4πラジアン）の時、Z軸を回すとこう見えます。

library("animation")
#アニメーションさせてみる。
TC00=seq(0,2*pi,length=Circle_Divide/2)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]
x<-rep(Circle_Divide/8*5,length=(Circle_Divide/2))
Time_Code<-complex(re=x,im=TC02)

saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo04.gif")

f:id:ochimusha01:20191011021350g:plain

どうしてやり方を変えたのかというと、ただ水平なだけの時（すなわちXY軸を0に固定時）は、Z軸の値がどんなに変化しても表か裏が延々と続くのみで面白くないからです。

「表の映像」のみが延々と続く退屈なアニメーション

TC00=seq(0,2*pi,length=Circle_Divide/2)
#アニメーションさせてみる。
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]
x<-rep(c(Circle_Divide-1,Circle_Divide,1,2),length=(Circle_Divide/2))
Time_Code<-complex(re=x,im=TC02)

saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo06.gif")

f:id:ochimusha01:20191011184632g:plain

「裏の映像」のみが延々と続く退屈なアニメーション

TC00=seq(0,2*pi,length=Circle_Divide/2)
#アニメーションさせてみる。
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]
x<-rep(c(Circle_Divide/2-1,Circle_Divide/2,Circle_Divide/2+1),length=(Circle_Divide/2))
Time_Code<-complex(re=x,im=TC02)

saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo06.gif")

f:id:ochimusha01:20191011184104g:plain

似た様な「表裏逆転の危機」は以下の状況でも観測されます。

f:id:ochimusha01:20191011184910j:plain

①Y軸とX軸を0に固定した時のX軸=±90度(±π/4ラジアン)前後（すなわちZ軸=±90度(±π/4ラジアン)固定時のXY軸±90度(±π/4ラジアン）前後）

XY軸90度(±π/4ラジアン)前後

library("animation")
#アニメーションさせてみる。
xy<-rep(c(Circle_Divide/4-1,Circle_Divide/4),length=(Circle_Divide/2))
zz<-rep(1,length=Circle_Divide/2)
Time_Code<-complex(re=xy, im=zz)
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo01.gif")

f:id:ochimusha01:20191011145749g:plain

XY軸-90度(±π/4ラジアン)前後

library("animation")
#アニメーションさせてみる。
xy<-rep(c(Circle_Divide/4*3-1,Circle_Divide/4*3),length=(Circle_Divide/2))
zz<-rep(1,length=Circle_Divide/2)
Time_Code<-complex(re=xy, im=zz)
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo01.gif")

f:id:ochimusha01:20191011150029g:plain

逆を言えば、両者の間が表（あるいは裏）の状態がスムーズに連続している状態となる訳ですね。

「表」の動きのみ抽出（X軸のみ回転時）

library("animation")
#アニメーションさせてみる。
TC00=seq(0,2*pi,length=Circle_Divide/2)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]

TC03a<-TC02[TC02>=Circle_Divide/4*3 &TC02<=Circle_Divide ]
TC03b<-TC02[TC02>=1 & TC02<=Circle_Divide/4 ]
xy<-c(TC03a,TC03b)
zz<-rep(1,length=Circle_Divide/2)
Time_Code<-complex(re=xy, im=zz)
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo08R.gif")

f:id:ochimusha01:20191011162254g:plain

「裏」の動きのみ抽出（X軸のみ回転時）

library("animation")
#アニメーションさせてみる。
xy<-seq(Circle_Divide/4+1,Circle_Divide/4*3-1,length=Circle_Divide/2)
zz<-rep(1,length=Circle_Divide/2)
Time_Code<-complex(re=xy, im=zz)
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo07L.gif")

f:id:ochimusha01:20191011164321g:plain

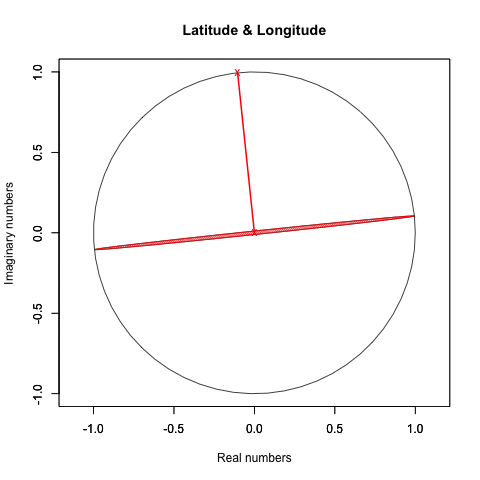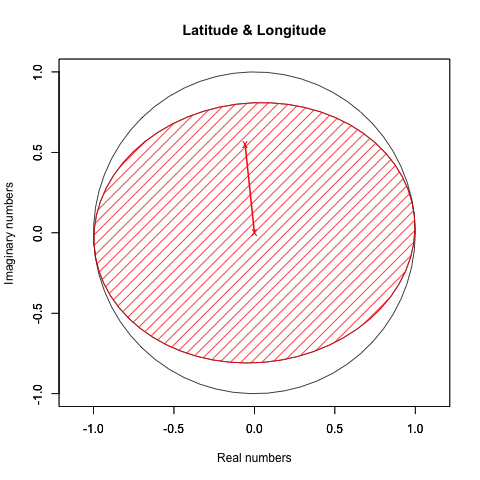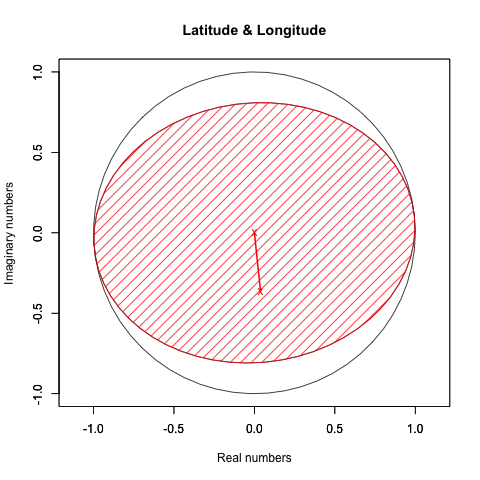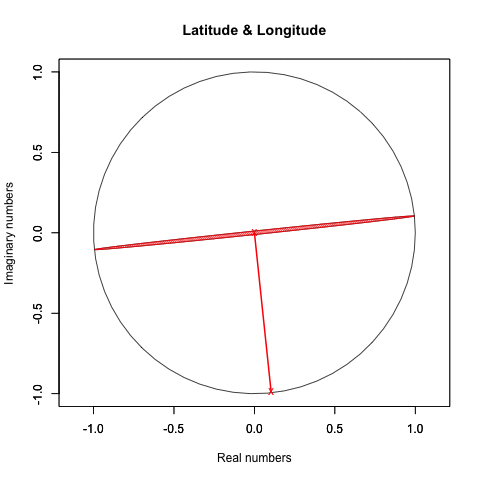
②X軸とZ軸を0に固定した時のY軸とY軸±90度(±π/4ラジアン)前後（すなわちZ軸=±90度(±π/4ラジアン)固定時のXY軸±90度(±π/4ラジアン）前後）

XY軸90度(±π/4ラジアン)前後

#アニメーションさせてみる。
xy<-rep(c(Circle_Divide/4-1,Circle_Divide/4),length=(Circle_Divide/2))
zz<-rep(Circle_Divide/4,length=Circle_Divide/2)
Time_Code<-complex(re=xy,im=zz)

saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo07.gif")

f:id:ochimusha01:20191011152127g:plain

XY軸-90度(±π/4ラジアン)前後

#アニメーションさせてみる。
xy<-rep(c(Circle_Divide/4*3-1,Circle_Divide/4*3),length=(Circle_Divide/2))
zz<-rep(Circle_Divide/4,length=Circle_Divide/2)
Time_Code<-complex(re=xy,im=zz)

saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo07.gif")

f:id:ochimusha01:20191011141028g:plain

逆を言えば、両者の間が表（あるいは裏）の状態がスムーズに連続している状態となる訳ですね。

「表」の動きのみ抽出（Y軸のみ回転時）

library("animation")
#アニメーションさせてみる。
TC00=seq(0,2*pi,length=Circle_Divide/2)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]

TC03a<-TC02[TC02>=Circle_Divide/4*3 &TC02<=Circle_Divide ]
TC03b<-TC02[TC02>=1 & TC02<=Circle_Divide/4 ]

tr01<-seq(Circle_Divide/4*3+1,Circle_Divide,length=Circle_Divide/4)
tr02<-seq(1,Circle_Divide/4-1,length=Circle_Divide/4)
xy<-c(tr01,tr02)
zz<-rep(Circle_Divide/4,length=Circle_Divide/2)
Time_Code<-complex(re=xy, im=zz)
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo07R.gif")

f:id:ochimusha01:20191011171034g:plain

「裏」の動きのみ抽出（Y軸のみ回転時）

library("animation")
#アニメーションさせてみる。
xy<-seq(Circle_Divide/4+1,Circle_Divide/4*3-1,length=Circle_Divide/2)
zz<-rep(Circle_Divide/4,length=Circle_Divide/2)
Time_Code<-complex(re=xy, im=zz)
saveGIF({
for (i in Time_Code){
　　Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo07L.gif")

f:id:ochimusha01:20191011171203g:plain

ここでいう「表裏逆転の危機」を、一般には「ジンバルロック問題」といいます。

ジンバル（Gimbal） - Wikipedia

1つの軸を中心として物体を回転させる回転台の一種。軸が直交するようにこれを設置すると、内側のジンバルに載せられたロータの向きを常に一定に保つことができる。例えば船舶や航空機に搭載された、ジャイロスコープ、羅針盤、焜炉、ドリンクホルダーなどが一般にジンバルを使って地平線に対して常に垂直を向くようになっている。

航空宇宙分野の慣性航法システムのジャイロにおけるジンバルなど、3軸の全てに自由な運動がある場合は、機体の回転によって3つのジンバルリングのうち2つの軸が同一平面上にそろってしまうジンバルロックという現象が発生しうる。発生すると、本来3あるはずの自由度が2になってしまう。この問題を回避するため、4番目のジンバルを追加するなどして、ジンバル間の角度を保つようにする。最近では、ジンバルを全く使わずに角(加)速度センサによって高精度に角(加)速度を検出し、それを計算機で数値積分し姿勢を逆算するという手法もある。

また物理的な問題ばかりではなく、慣性航法システムのコンピュータプログラムや3次元コンピュータグラフィックスなどにおいて、オイラー角で3次元の姿勢を表現する場合にも全く同様の問題があり、それらで発生する問題もジンバルロックと呼んでいる。表現においては、四元数を使うのが回避法のひとつである。

これについて、様々な人が様々な主張を展開しているのでまとめてみる事にしました。

*1:xy_radian%/%(Circle_Divide/4)==1 ||xy_radian%/%(Circle_Divide/4)==2),LR_color<-rgb(1,0,0),LR_color<-rgb(0,1,0