三角関数や自然対数を使って円が描ける様になると、ちょっとした応用でどんな正多角形も描ける様になります。
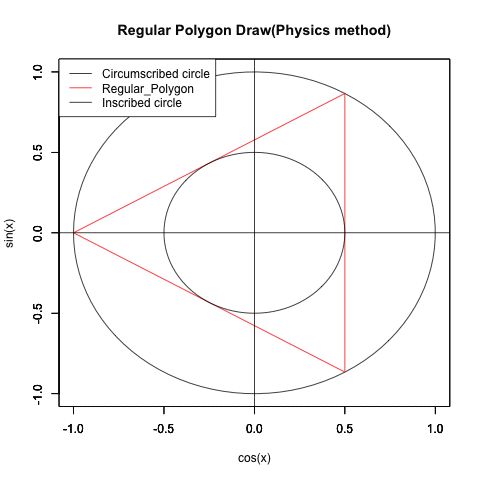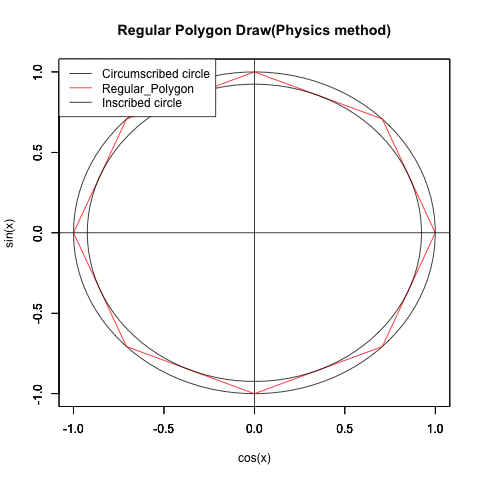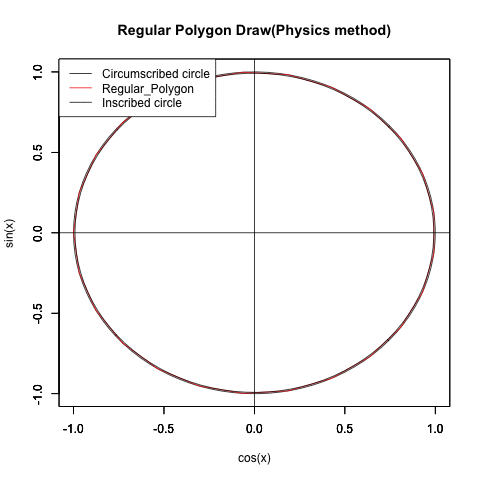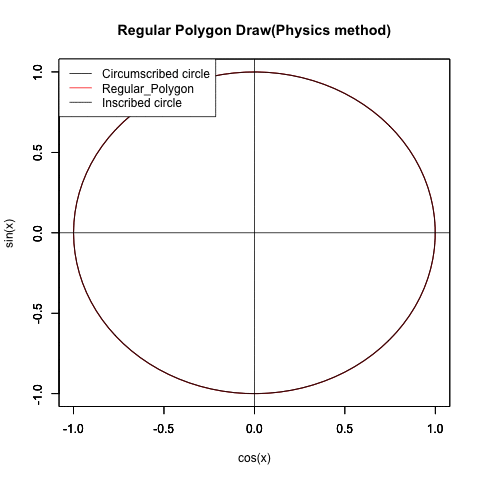
すると今度は内接円(Inscribed circle)の半径(Radius)を下限、外接円(Circumscribed circle)の半径を上限とする拡大縮小を伴った多角形の回転に直面する展開を迎えます。


正式名称は知りませんが、とりあえず私はこれを「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」と呼んでいます。何故かというと…

内接円(Inscribed circle)の半径(Radius)を下限、外接円(Circumscribed circle)の半径を上限とする拡大縮小を伴った多角形の回転は以下のルールに従う。

①「辺長=2π/辺数」が出発点となる。
- 一辺の長さがaの正N角形に内接する円の半径r
r=a*(2*tan(pi/N))
a=r/(2*tan(pi/N)) - 一辺の長さがaの正N角形に外接する円の半径R
R=a/(2*tan(pi/N))/cos(pi/N)
a=R*(2*tan(pi/N))/cos(pi/N)
②「サンプリング」の元波形となるのは辺数分だけ位相がマイナス方向にズレたコサイン波cos(θ-1/辺数*π)で、サンプリング範囲は0から2/辺数*π。サンプリングされた波形は辺数だけ繰り返される。
③サンプリング波形の頂点は辺長/2、その時の値は外接円の半径(単位円の場合は1)にその多角形の内接円と外接円の差を加えた結果となる。位相幾何学(Topology)的にトーラス(単数形torus, 複数形tori)形状と看做すとこう見える。

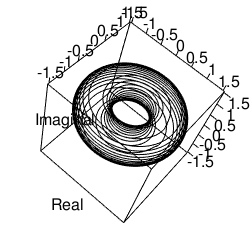

具体的にグラフ化してみたのが以下となります。

統計言語Rによる「サンプリング元」の作図
#RIC=内接円の角度(Radians of Inscribed Circle)
#Noc=角数(Number of corners)
RIC<-function(NoC){
f0<-function(x){cos(x)}
plot(f0,col=rgb(0,1,1),xlim=c(0,2*pi),ylim=c(-1,1),main="Radians of Inscribed Regular Polygons",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){cos(x-1/NoC*pi)}
plot(f1,col=rgb(0,0,1),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
abline(v =0)for(i in 1:NoC){
abline(v =2*i/NoC*pi)
}
#補助線
abline(h=1,col=rgb(1,0,0))
abline(h=cos(pi/NoC),col=rgb(0,1,0))#サンプリング範囲を塗りつぶす
polygon(c(0,2/NoC*pi,2/NoC*pi,0,0), #x
c(1,1,cos(pi/NoC),cos(pi/NoC),1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色text01<-paste0("y=cos(θ-1/",NoC,"*pi)")
legend("bottomright", legend=c("y=cos(θ)",text01,"Radius of Unit Circle","Radius of Inscribed circle"), lty=c(1,1,1,1), col=c(rgb(0,1,1),rgb(0,0,1),rgb(1,0,0),rgb(0,1,0)))
}
#アニメーション
library("animation")
Time_Code=rep(2:16, each=3)
saveGIF({
for (i in Time_Code){
RIC(i)
}
}, interval = 0.1, movie.name = "RIC01.gif")
切り取られる波形は「概ね」相似関係にあります。
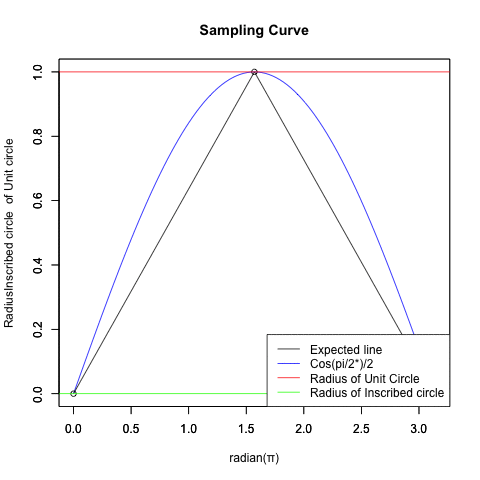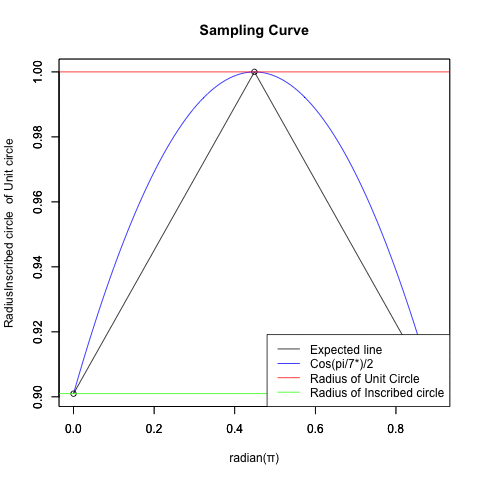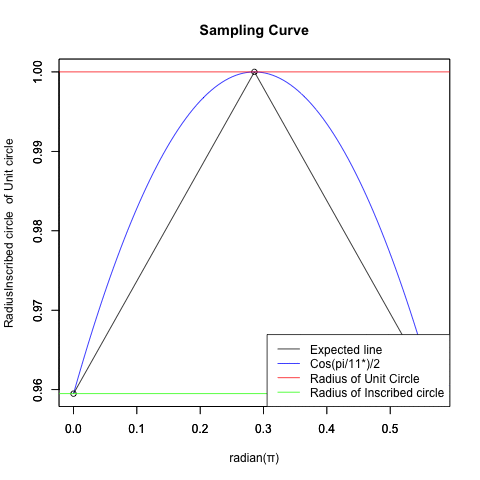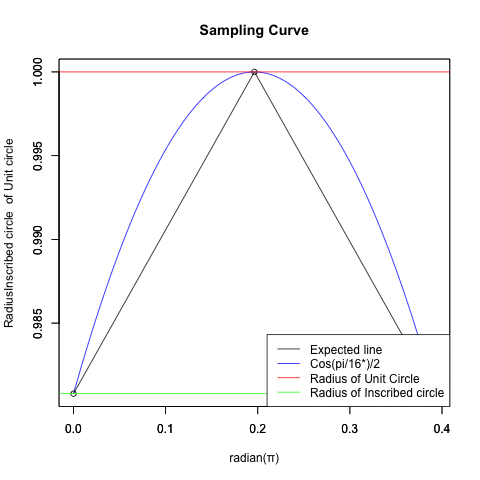
統計言語Rによる「欲しいサンプリング結果」の作図
#SC=サンプリングされた曲線(Sampling Curve)
#Noc=角数(Number of corners)
SC<-function(NoC){
f0<-function(x){cos(x-1/NoC*pi)}
plot(f0,col=rgb(0,0,1),xlim=c(0,2*pi/NoC),main="Sampling Curve",xlab="radian(π)",ylab="RadiusInscribed circle of Unit circle")
par(new=T) #上書き
#期待線
c0<-seq(0,2/NoC*pi,length=3)
c1<-c(cos(pi/NoC),1,cos(pi/NoC))
plot(c0,c1,col=rgb(0,0,0),type="o",xlim=c(0,2*pi/NoC),main="",xlab="",ylab="")#外接円=内接円による境界線
abline(h=1,col=rgb(1,0,0))
abline(h=cos(pi/NoC),col=rgb(0,1,0))
#凡例
text01<-paste0("Cos(pi/",NoC,"*)/2")
legend("bottomright", legend=c("Expected line",text01,"Radius of Unit Circle","Radius of Inscribed circle"), lty=c(1,1,1,1), col=c(rgb(0,0,0),rgb(0,0,1),rgb(1,0,0),rgb(0,1,0)))}
#アニメーション
library("animation")
Time_Code=rep(2:16, each=3)
saveGIF({
for (i in Time_Code){
SC(i)
}
}, interval = 0.1, movie.name = "SC01.gif")
実際には辺数だけ「サンプリングされた波形の再生」が遂行されます。
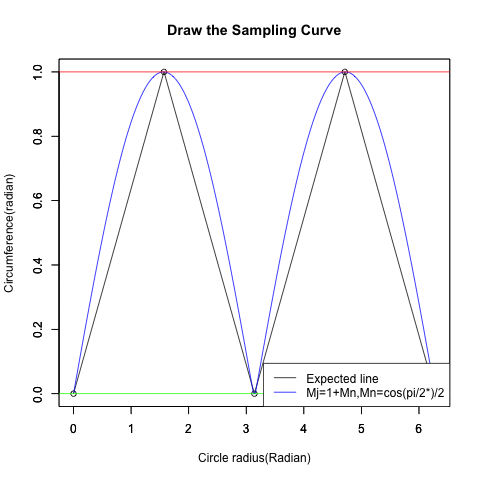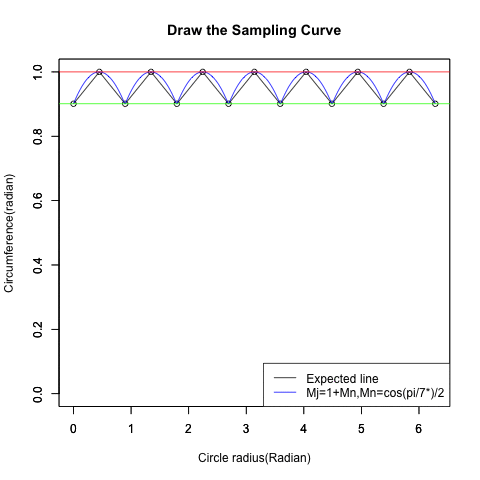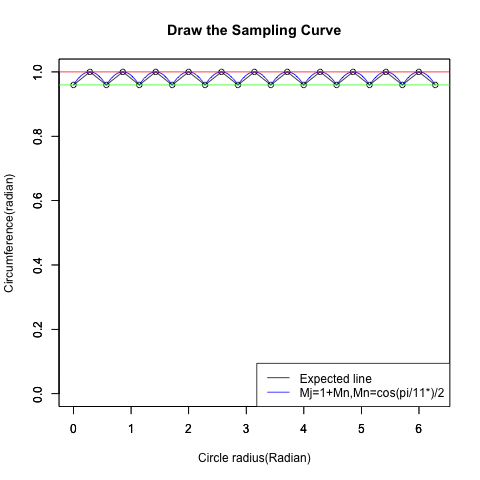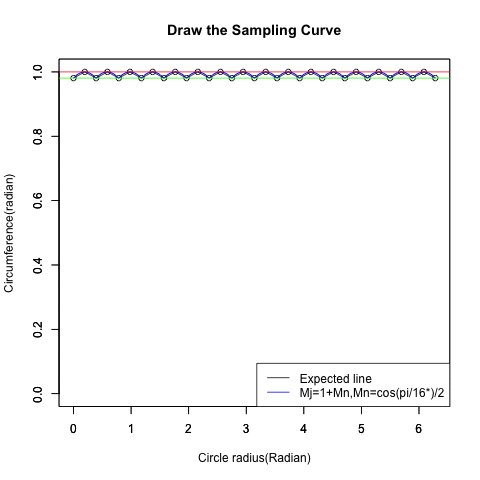
統計言語Rによる「サンプリング再生過程」の作図
#DSC=サンプリング再生過程(Draw the Sampling Curve)
#NoC=角数(Number of corners)
DSC<-function(NoC){
#期待線
c0<-seq(0,2*pi,length=NoC*2+1)
c1<-cos(pi/NoC)
for(i in 1:NoC-1){
c1=c(c1,1,cos(pi/NoC))
}
plot(c0,c1,type="o",xlim=c(0,2*pi),ylim=c(0,1),main="Draw the Sampling Curve",ylab='Circumference(radian)', xlab='Circle radius(Radian)')
#サンプリング線
par(new=T) #上書き
DN<-100 #分割数(Division Number)
R_time=seq(0,2*pi,length=NoC*DN)
Smp_time=seq(0,2/NoC*pi,length=DN)
f0<-function(x){cos(x-1/NoC*pi)}
S_data<-NULL
for(i in 1:NoC){
S_data<-c(S_data,f0(Smp_time))
}
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0,1),col=rgb(0,0,1),main="",ylab="", xlab="")
#外接円=内接円による境界線
abline(h=1,col=rgb(1,0,0))
abline(h=cos(pi/NoC),col=rgb(0,1,0))
#凡例
text01<-paste0("Mj=1+Mn,Mn=cos(pi/",NoC,"*)/2")
legend("bottomright", legend=c("Expected line",text01), lty=c(1,1), col=c(rgb(0,0,0),rgb(0,0,1)))
}#アニメーション
library("animation")
Time_Code=rep(2:16, each=3)
saveGIF({
for (i in Time_Code){
DSC(i)
}
}, interval = 0.1, movie.name = "DSC01.gif")
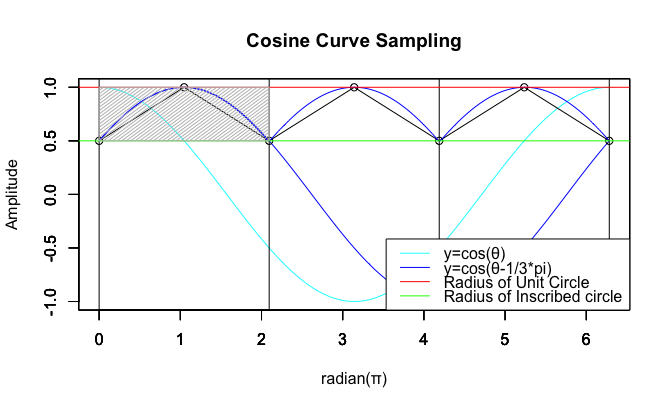
全体像を把握する為に一緒に表示したパターン。
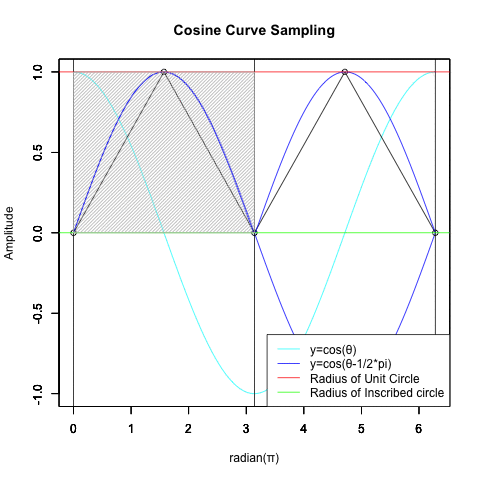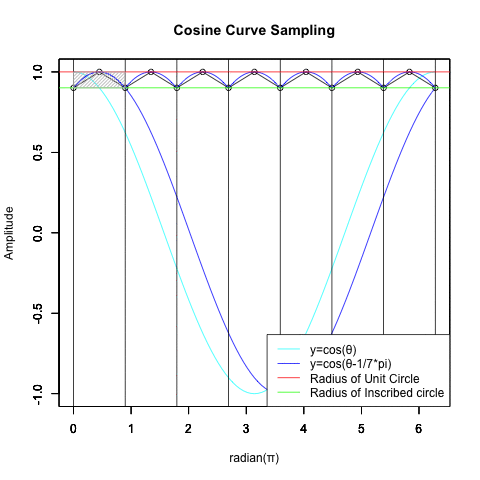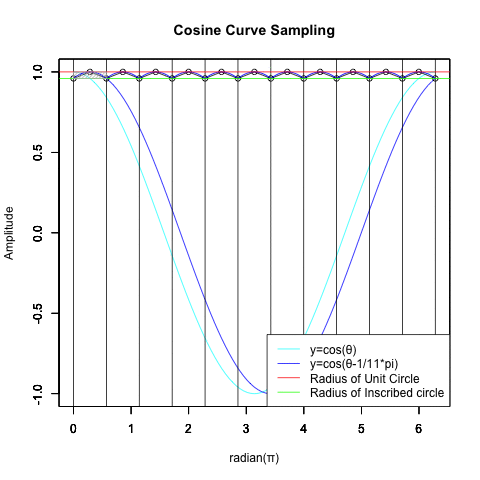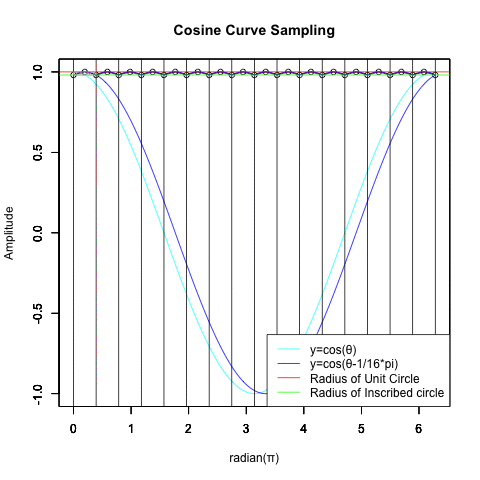
統計言語Rによる「サンプリング元」の作図
#CCS=コサイン曲線のサンプリン(Cosine Curve Sampling)
#Noc=角数(Number of corners)
CCS<-function(NoC){
f0<-function(x){cos(x)}
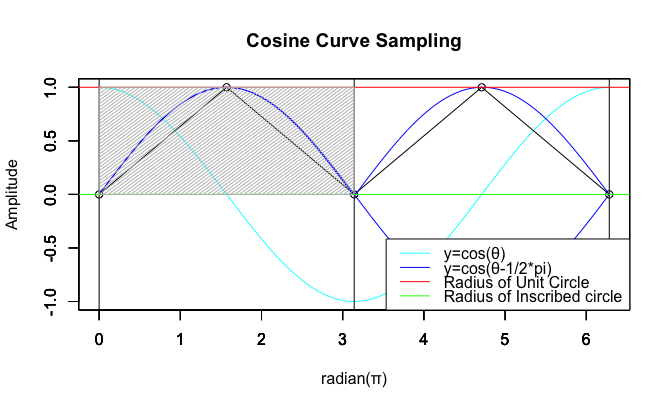
plot(f0,col=rgb(0,1,1),xlim=c(0,2*pi),ylim=c(-1,1),main="Cosine Curve Sampling",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){cos(x-1/NoC*pi)}
plot(f1,col=rgb(0,0,1),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き#期待線
c0<-seq(0,2*pi,length=NoC*2+1)
c1<-cos(pi/NoC)
for(i in 1:NoC-1){
c1=c(c1,1,cos(pi/NoC))
}
plot(c0,c1,type="o",xlim=c(0,2*pi),ylim=c(-1,1),main="",ylab="", xlab="")
#サンプリング線
par(new=T) #上書き
DN<-100 #分割数(Division Number)
R_time=seq(0,2*pi,length=NoC*DN)
Smp_time=seq(0,2/NoC*pi,length=DN)
f0<-function(x){cos(x-1/NoC*pi)}
S_data<-NULL
for(i in 1:NoC){
S_data<-c(S_data,f0(Smp_time))
}
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(-1,1),col=rgb(0,0,1),main="",ylab="", xlab="")
#補助線abline(v =0)
for(i in 1:NoC){
abline(v =2*i/NoC*pi)
}
abline(h=1,col=rgb(1,0,0))
abline(h=cos(pi/NoC),col=rgb(0,1,0))#サンプリング範囲を塗りつぶす
polygon(c(0,2/NoC*pi,2/NoC*pi,0,0), #x
c(1,1,cos(pi/NoC),cos(pi/NoC),1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#凡例
text01<-paste0("y=cos(θ-1/",NoC,"*pi)")
legend("bottomright", legend=c("y=cos(θ)",text01,"Radius of Unit Circle","Radius of Inscribed circle"), lty=c(1,1,1,1), col=c(rgb(0,1,1),rgb(0,0,1),rgb(1,0,0),rgb(0,1,0)))
}
#アニメーション
library("animation")
Time_Code=rep(2:16, each=3)
saveGIF({
for (i in Time_Code){
CCS(i)
}
}, interval = 0.1, movie.name = "CCS01.gif")
今度はそれぞれの図形についてみていきましょう。ここで表面化してくるのが「90度単位の特別性」なる概念。元波形たるCos(θ)波と、位相が90度(1/2πラジアン)ズレたSin(θ)波が直交すれば円を描き、逆にCos(θ)波とCos(θ)波あるいは-Cos(θ)波との組み合わせは観測結果を水平化(Flatline)させてしまいます。
- 0度=0ラジアン…正1角形(Regular Henagon)に登場。
- 180度=πラジアン…正2角形(Regular Digon)に登場。
- 90度=1/2πラジアン…正方形(Square)に登場。
- 360度=2πラジアン…円そのもの(Circle itself)に登場。
①円そのもの(Circle itself)の場合
以下に述べる「正多角形群全ての観測システム上の原型」となるので、最初に提示しておく事にする。
*プログラム中においては既に当然の様に円描写に「Cos(θ)波とSin(θ)波の直交」を用いているが、実際にそのシステム全体における意味付けが明らかとなるのは、ここでの「正多角形群全ての観測」が終わってからとなる点に注意しなければならない。
統計言語Rによるプログラミング例
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",main="Circle itself",xlab="cos(θ)",ylab="sin(θ)")

円そのもの(Circle itself)の「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」に基づく諸元は以下。
- 理論上辺数=無限大、辺数=無限小。実際の単位円(Unit Circle, 半径1の円弧)上における中心からの任意の分割数(Division Number)による計測結果を2Dヒストグラム(度数分布表)に表すと空間的広がり=仮想分割数*周期数に対応した半径(単位円では1)の集合、時間的広がり=観測開始から観測度数Count Upに至る周期=分割数が得られる。

こうした観測結果より得られた時空間認識から単位円柱(Unit cylinder=半径1,周期1)が構成可能となる。
統計言語Rによるプログラミング例
library(rgl)
Rtime<-seq(0,2*pi,length=60)
CosX<-cos(Rtime)
SinY<-sin(Rtime)
plot3d(CosX,SinY,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2*pi))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01")

- 「サンプリング」の元波形となるのはコサイン波cos(θ-1/無限大)=cos(θ)でオリジナルの波形たるコサイン波cos(θ)と完全に重なる。サンプリング範囲は0から2/無限大*π=無限大で実質上円周と同じ2π。
統計言語Rによるプログラミング例。
cx<-seq(0,2*pi,length=60)
cy<-cos(c0)
plot(cx,cy,type="l",main="Trajectory of Circle itself",xlab="Amplitude",ylab="Radians")
#凡例
legend("bottomright", legend=c("cos(θ)"), lty=c(1), col=c(rgb(0,0,0)))
もちろんCos(θ)波とCos(θ)波を直交させても、それ単体ではあまり面白い観測結果とはなり得ない。統計言語Rによるプログラミング例。
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)
plot(cx,cy,type="o",main="Cos(θ) orthogonal Cos(θ) ",xlab="cos(θ)",ylab="cos(θ)")
#凡例
legend("bottomright", legend=c("cos(θ) orthogonal cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))
- サンプリング波形の値は外接円の半径(単位円の場合は1)+内接円と外接円の差(常に0)なので頂点位置は存在しない。
*上掲の様に観測結果が以下だから仕方がない。

そう、正多角形の極限としての円そのもの(Circle itself)の最大の特徴は「内接円と外接円の差が0」である点にあるので位相幾何学(Topology)的にトーラス(単数形torus, 複数形tori)形状を考えると以下の様になってしまうのである。

②正1角形(Regular Henagon)の場合
平面上には描画可能な(あるいは立体との接点としてのみ映る)図形。ところで数学界には円周を2πでなく1τ(タウ)で表すべきとする立場もある。
角度をラジアン(弧度法)で表記したとき、「1周=τ」と表せるのが最大の利点である。
現在は高校の数学Ⅱで弧度法を学習するが、πが「半周」であることに違和感を覚えた人は多いだろう。
例えば、45°は1/8周なのに、πを使うと1/4πと表記しなければならない。τを使えば、1/8周は1/8τであり、直感的である。
実際のところどうなのだろう。とりあえず「どのタイミングで観測しても観測結果が必ず2π=1τとなる球面上の唯一の点(観測原点あるいは観測対象)が等速円運動している」と仮定してみる。
統計言語Rによるプログラミング例
#RH=1角形(Regular Henagon)
#Radian=角度(60分割)
RH<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",main="Regular Henagon",xlab="cos(θ)",ylab="sin(θ)")
text(cx[Radian],cy[Radian],"X",col=rgb(1,0,0))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
RH(i)
}
}, interval = 0.1, movie.name = "RH01.gif")

普通に考えると球面上の対応する動きはこうなる。
実際にはこういう動きをしてるかもしれないが、何しろそれを確かめる手段がないのである。むしろ「球面上の任意の位置に唯一の点(観測原点あるいは観測対象)が確率的に存在している」と捉えた方が状況を正確に要約してると言えるかもしれない。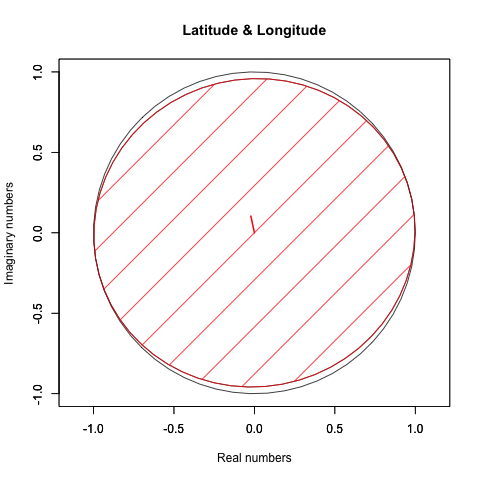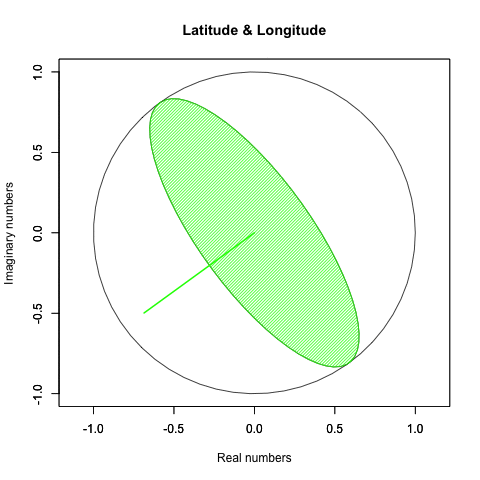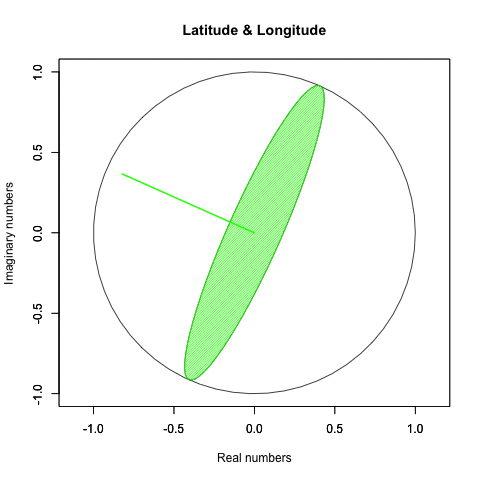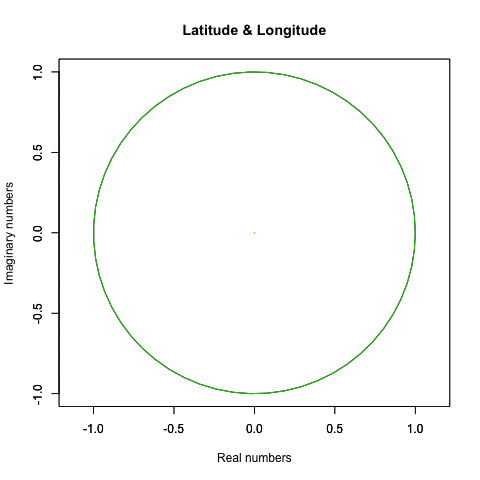
とりあえず「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」に基づく諸元は以下となる。
- 単位円(Unit Circle, 半径1の円弧)上においては辺数=1、辺長(2π/辺数)=2πあるいは1τ。球面上にのみ描画可能。
- 「サンプリング」元波形はcos(θ-π)=-cos(θ)でサンプリング範囲が0からπに及ぶので繰り返されない。オリジナル波形cos(θ)と合成すると完全に打ち消しあって水平化(Flatline)する。
統計言語Rによるプログラミング例。
cx<-seq(0,2*pi,length=60)
cy1<-cos(c0)*-1
plot(cx,cy1,type="l",main="Trajectory of Regular Henagon",xlab="Radians",ylab="Amplitude")par(new=T) #上書き
cy2<-cos(cx)
plot(cx,cy2,type="l",col=rgb(0,0,1),main="",xlab="",ylab="")
par(new=T) #上書き
cy3<-cos(cx)-cos(cx)
plot(cx,cy3,type="l",col=rgb(1,0,0),main="",xlab="",ylab="")
#凡例
legend("bottomright", legend=c("Sampling_wave=-cos(θ)","Origin_wave=cos(θ)","Sampling_wave+Origin_wave"), lty=c(1,1,1), col=c(rgb(0,0,0),rgb(0,0,1),rgb(1,0,0)))
もちろんCos(θ)波と-Cos(θ)波を直交させても、それ単体ではあまり面白い観測結果とはなり得ない。
統計言語Rによるプログラミング例。
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)*-1
plot(cx,cy,type="o",main="Cos(θ) orthogonal -Cos(θ) ",xlab="cos(θ)",ylab="-cos(θ)")
#凡例
legend("bottomright", legend=c("cos(θ) orthogonal -cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))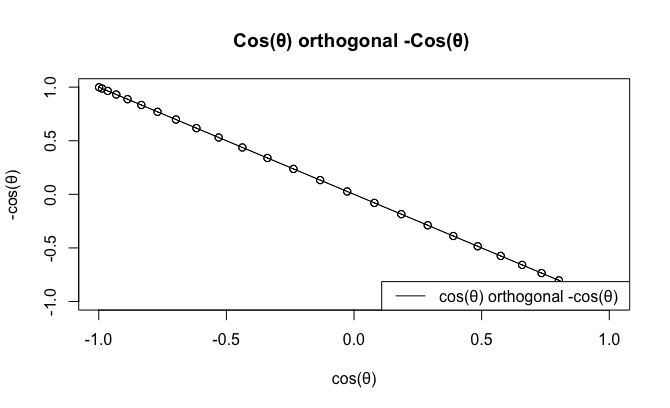
- あらゆる観測結果が水平化(Flatline)する為、サンプリング波形の頂点は計測不能、その値は全て外接円の半径(単位円の場合は1)そのものとなる。
位相幾何学(Topology)的にトーラス(単数形torus, 複数形tori)形状と看做す時は、概ね円そのもの(Circle itself)の特徴の真逆が割り振られる。
③正2角形(Regular Digon)の場合
やはりこれも平面上には描画可能な(あるいは立体との接点としてのみ映る)図形。
2つの点とその間を結ぶ「辺」で構成されるが、興味深いことにこの「辺」の概念がユークリッド幾何学上の線分の条件を満たしておらず「分割数に応じた同じ辺長(最大π)の線分の集合としてしか扱えない」というか「球面上の任意の位置に2点間を結ぶ同じ辺長(最大π)の直線が確率的に存在している」という状態。この巾着袋めいた動きこそが実は地球儀における緯度(Latitude)概念や共益複素数(Conjugate complex number)概念の大源流でもある。
位相のズレが90度(1/2πラジアン)単位なのでSin(θ)波が直交して円を描く。
*ただし「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」の制約で1/2のみ。これを2回繰り返す。
統計言語Rによるプログラミング例
#RD=2角形(Regular Digon)
#Radian=角度(60分割)
RD<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",main="Regular Henagon",xlab="cos(θ)",ylab="sin(θ)")p_max<-15
p0<-seq(pi,0,length=p_max)
px_Hi<-rev(cos(p0))
px_Low<-rev(cos(p0*-1))
py_Hi<-rev(sin(p0))
py_Low<-rev(sin(p0*-1))#左側インジケータ描画(緑)
polygon(c(px_Hi[1:Radian],px_Low[Radian:1]), #x
c(py_Hi[1:Radian],py_Low[Radian:1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
#右側インジケータ描画(赤)
polygon(c(px_Hi[p_max:Radian],px_Low[Radian:p_max]), #x
c(py_Hi[p_max:Radian],py_Low[Radian:p_max]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
}
#アニメーション
library("animation")
Time_Code=c(1:15,14:1)
saveGIF({
for (i in Time_Code){
RD(i)
}
}, interval = 0.1, movie.name = "RD01.gif")

正2角形(Regular digon)の「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」に基づく諸元は以下。
面白い観測結果が得られるのは正1角形と正2角形の間が最初となる。
統計言語Rによるプログラミング例。
#FHtD=1角形から2角形へ(From Henagon to Digon)
#Noc=角数(Number of corners), この場合1-2
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)
#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}
#アニメーション
library("animation")
Time_Code=seq(1,2, length=11)
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")
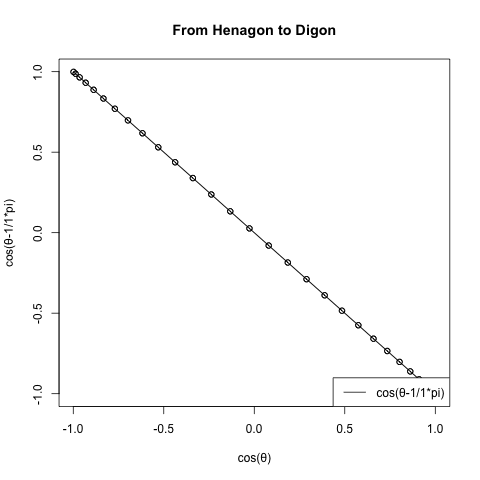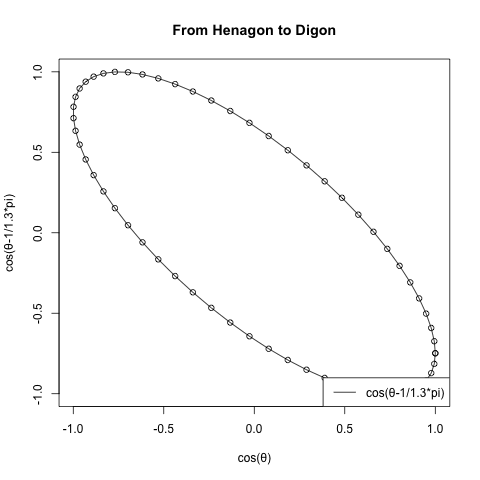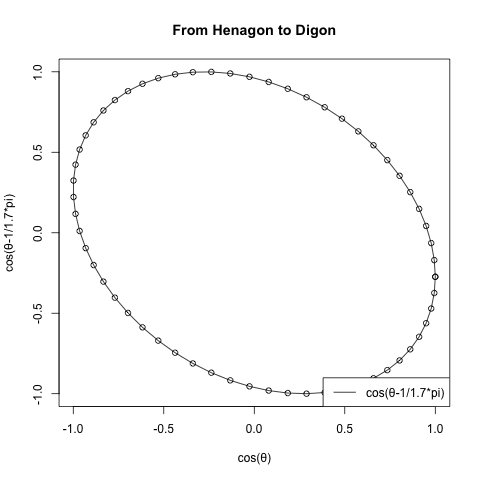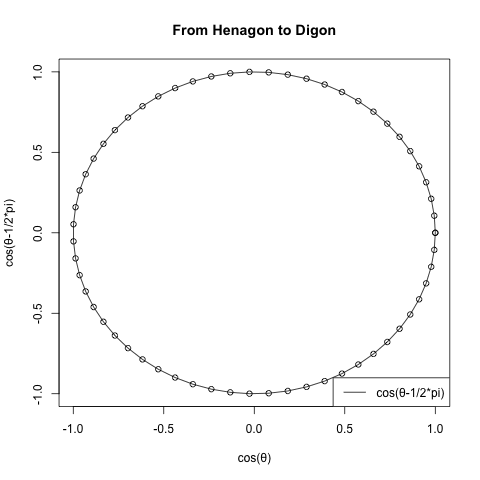
中心から補助線を引いてみた。
#FHtD=1角形から2角形へ(From Henagon to Digon)
#Noc=角数(Number of corners), この場合1-2
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)#中心からの補助線
cx0<-rep(0, length=length(cx))
cy0<-rep(0, length=length(cy))
segments(cx0, cy0, cx, cy,col=c(200,200,200))#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}
#アニメーション
library("animation")
Time_Code=c(seq(1,6, length=50),seq(6,64,length=20))
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")

とりあえずX軸とY軸を入れ替えてみたが何も変わらない。
#FHtD=1角形から2角形へ(From Henagon to Digon)
#Noc=角数(Number of corners), この場合1-2
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0-1/NoC*pi)
cy<-cos(c0)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab=text01,ylab="cos(θ)")#中心からの補助線
cx0<-rep(0, length=length(cy))
cy0<-rep(0, length=length(cx))
segments(cx0, cy0, cx, cy,col=c(200,200,200))#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}
#アニメーション
library("animation")
Time_Code=c(seq(1,6, length=50),seq(6,64,length=20))
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")
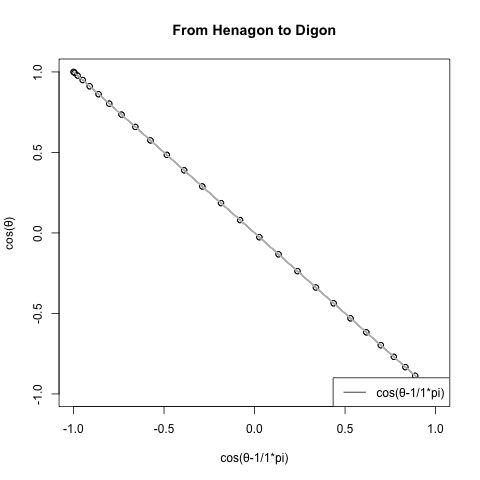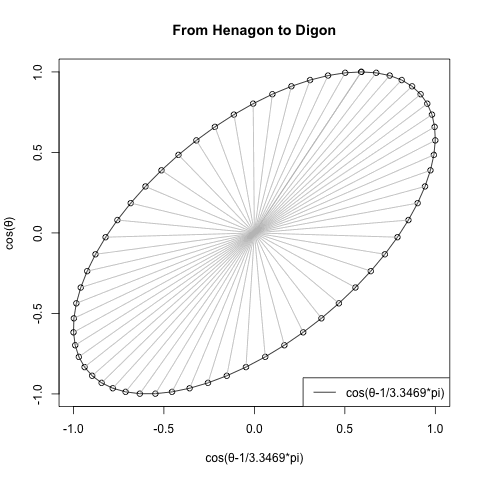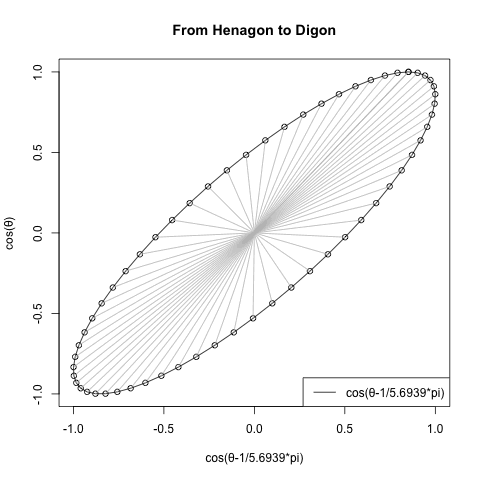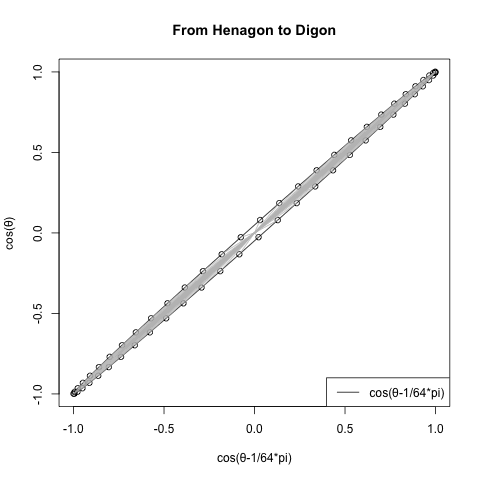
1以下の領域に手を出してみた。
#FHtD=1角形から2角形へ(From Henagon to Digon)
#Noc=角数(Number of corners), この場合1-2
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,asp=1,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)#中心からの補助線
cx0<-rep(0, length=length(cx))
cy0<-rep(0, length=length(cy))
segments(cx0, cy0, cx, cy,col=c(200,200,200))#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}
#アニメーション
library("animation")
Time_Code=seq(1,0.1,length=41)
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")
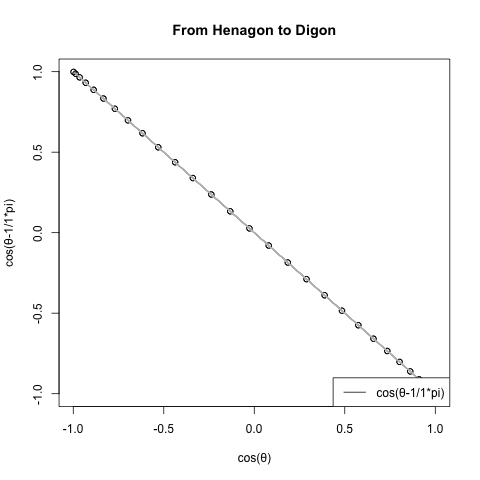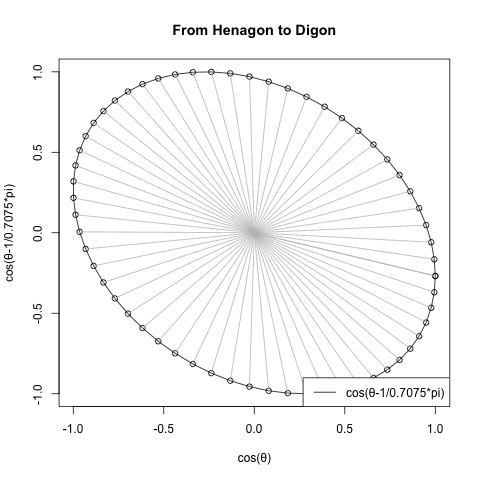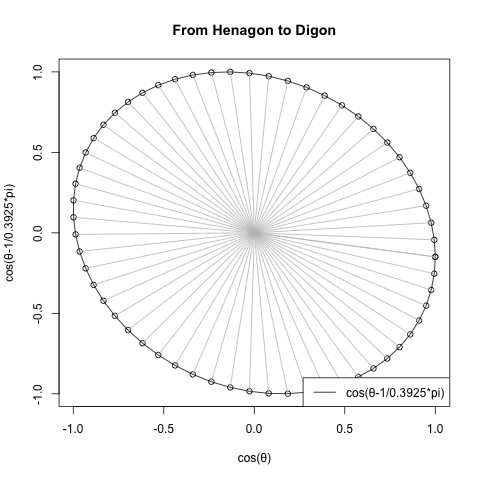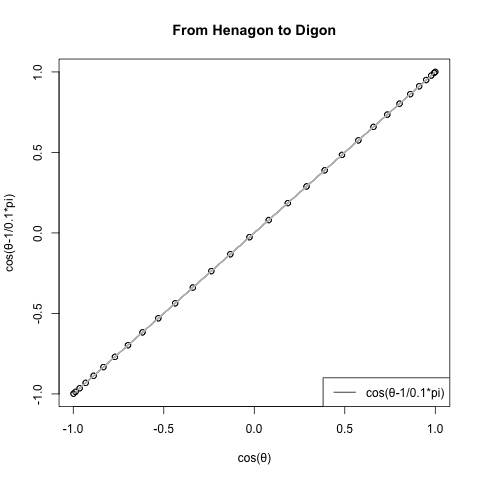
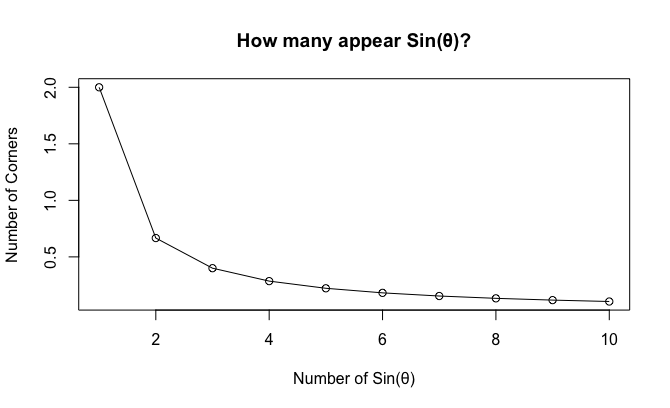
cos(θ-π/角数)。1以上では2のみしか現れないSin(θ)が、1以下の小数点下では0.1までに9個も現れる。
cy<-c(2,2/3,2/5,2/7,2/9,2/11,2/13,2/15,2/17,2/19)
cx<-c(1:length(cy))
plot(cx,cy,type="o",main="How many appear Sin(θ)?",xlab="Number of Sin(θ)",ylab="Number of Corners")
全体像としては以下の様になっている事が想定される。
- オリジナル波形Cos(θ)に対して正1角形のサンプリング波形は-Cos(θ)となり、観測結果を直交させると直線上に分布する。

- 正2角形のサンプリング波形はSin(θ)であり、その観測結果をオリジナル波形Cos(θ)オリジナル波形直交させると円を描く。この時の円周の最大値が2π。正多角形の辺数を無限に増やし、内接円と外接円の半径差を無限に0に近づけていった場合の極限値でもある。

- 以降のサンプリング波形は次第に円そのもののサンプリング波形であるCos(θ)(観測結果を直交させるとやはり直線上に分布)への無限収束を続ける。
統計言語Rによるプログラミング例。
#アニメーション
library("animation")
Time_Code=seq(1,48, length=96)
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")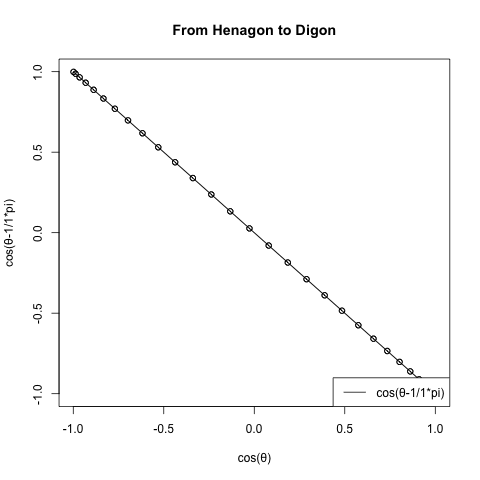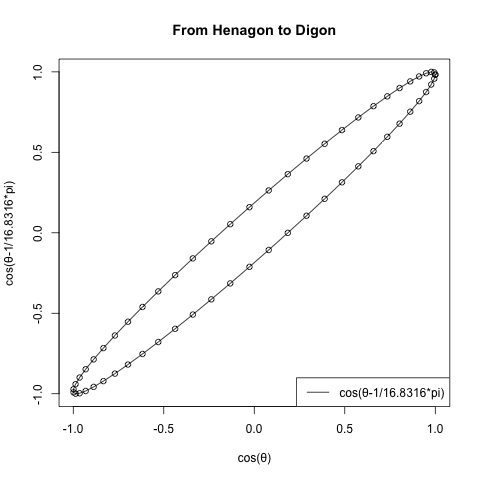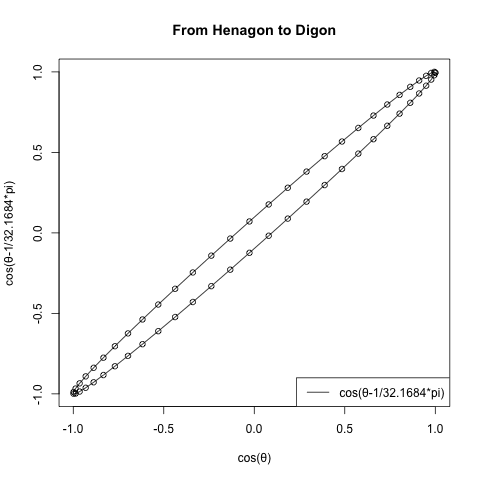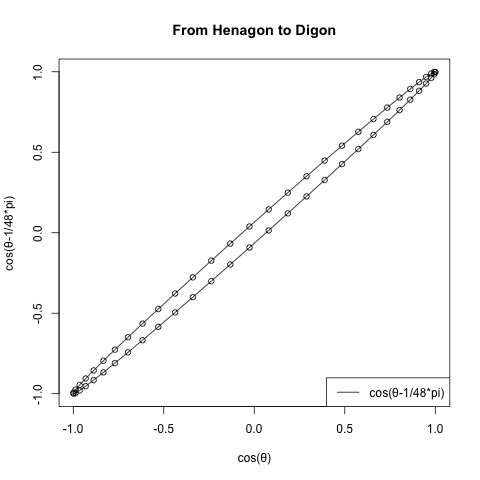

位相幾何学(Topology)的にトーラス(単数形torus, 複数形tori)形状と看做す時は以下となります。
③正三角形(Equilateral triangle)の場合

正3角形(Equilateral triangle)の「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」に基づく諸元は以下。

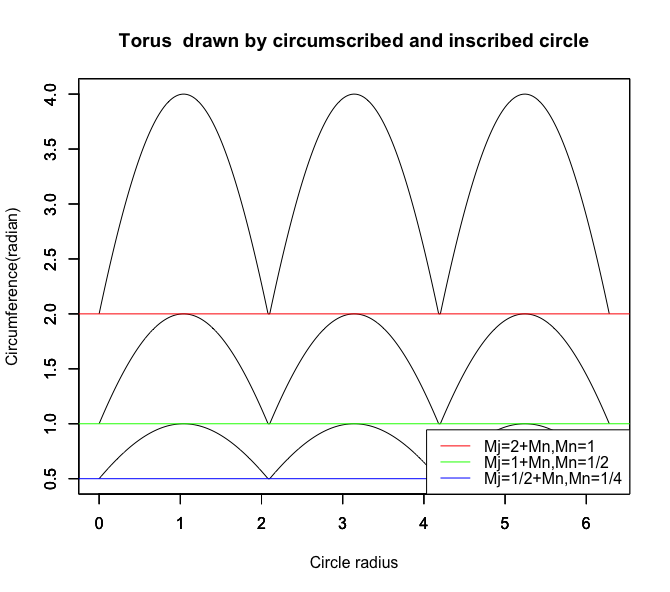
内接円と外接円の比率が対数規則を満たす等比数列なので「連続トーラス(Multiplex Tori)」を構築する。
大円(Major Circle)も小円(Miner Circle)も外接円/内接円、外接多角形/内接多角形の同心構造を備える重層的構造は、まさに華厳経でいう所の「海印三昧」の境地とも?
状況から予想される平面トーラス遷移図
c0=seq(0,2*pi,length=7)
c1=c(2,4,2,4,2,4,2)
c2=c(1,2,1,2,1,2,1)
c3=c(1/2,1,1/2,1,1/2,1,1/2)
plot(c0,c1,type="o",xlim=c(0,2*pi),ylim=c(1/2,4),ylab='x', xlab='y')
par(new=T) #上書き
plot(c0,c2,type="o",xlim=c(0,2*pi),ylim=c(1/2,4),ylab='', xlab='')
par(new=T) #上書き
plot(c0,c3,type="o",xlim=c(0,2*pi),ylim=c(1/2,4), main="Expected Multilayered Tori", ylab='', xlab='')
#外接円=内接円による境界線
abline(h=2,col=rgb(1,0,0))
abline(h=1,col=rgb(0,1,0))
abline(h=0.5,col=rgb(0,0,1))
#凡例
legend("bottomright", legend=c("Mj=2+Mn,Mn=1","Mj=1+Mn,Mn=1/2","Mj=1/2+Mn,Mn=1/4"), lty=c(1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))

統計言語Rによる「サンプリング結果のマッピング」
R_time=seq(0,2*pi,length=300)
Smp_time=seq(0,2/3*pi,length=100)#標準円(半径0.5→1)
f0<-function(x){cos(x-1/3*pi)}
S_data<-c(f0(Smp_time),f0(Smp_time),f0(Smp_time))
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,4),main="Torus drawn by circumscribed and inscribed circle",ylab='Circumference(radian)', xlab='Circle radius')
#半径1→2
par(new=T) #上書き
S_data<-c(f0(Smp_time)*2,f0(Smp_time)*2,f0(Smp_time)*2)
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,4),ylab='', xlab='')#半径2→4)
par(new=T) #上書き
S_data<-c(f0(Smp_time)*4,f0(Smp_time)*4,f0(Smp_time)*4)
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,4),ylab='', xlab='')
#外接円=内接円による境界線
abline(h=2,col=rgb(1,0,0))
abline(h=1,col=rgb(0,1,0))
abline(h=0.5,col=rgb(0,0,1))
#凡例
legend("bottomright", legend=c("Mj=2+Mn,Mn=1","Mj=1+Mn,Mn=1/2","Mj=1/2+Mn,Mn=1/4"), lty=c(1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1)))
④正方形(Square)の場合
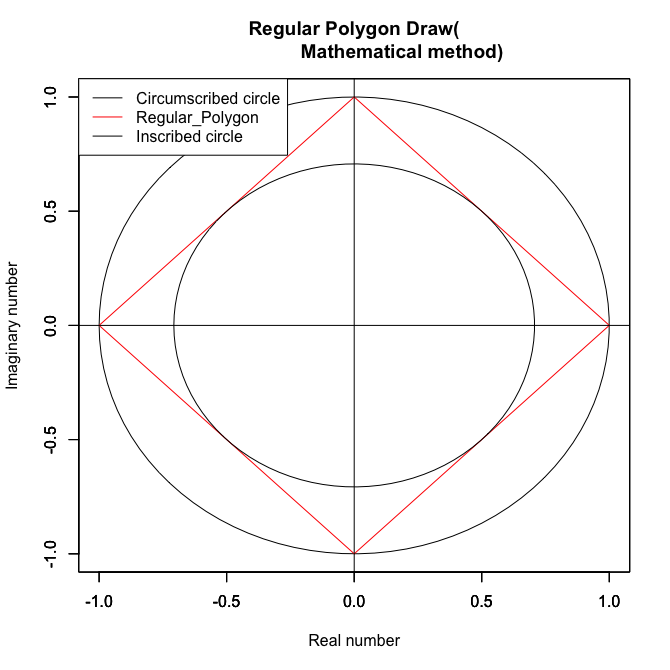
正方形(Square)の「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」に基づく諸元は以下。


内接円と外接円の比率が対数規則を満たす等比数列なので「連続トーラス(Multiplex Tori)」を構築する。
大円(Major Circle)も小円(Miner Circle)も外接円/内接円、外接多角形/内接多角形の同心構造を備える重層的構造は、まさに華厳経でいう所の「海印三昧」の境地とも?
状況から予想される平面トーラス遷移図
c0=seq(0,2*pi,length=9)
c1=c(sqrt(2),2,sqrt(2),2,sqrt(2),2,sqrt(2),2,sqrt(2))
c2=c(1,sqrt(2),1,sqrt(2),1,sqrt(2),1,sqrt(2),1)
c3=c(sqrt(2)/2,1,sqrt(2)/2,1,sqrt(2)/2,1,sqrt(2)/2,1,sqrt(2)/2)
plot(c0,c1,type="o",xlim=c(0,2*pi),ylim=c(sqrt(2)/2,2),main="Expected Multilayered Tori",ylab='x', xlab='y')
par(new=T) #上書き
plot(c0,c2,type="o",xlim=c(0,2*pi),ylim=c(sqrt(2)/2,2),main="",ylab='', xlab='')
par(new=T) #上書き
plot(c0,c3,type="o",xlim=c(0,2*pi),ylim=c(sqrt(2)/2,2),main="",ylab='', xlab='')
#外接円=内接円による境界線
abline(h=2,col=rgb(1,0,0))
abline(h=sqrt(2),col=rgb(0,1,0))
abline(h=1,col=rgb(0,0,1))
abline(h=1/sqrt(2),col=rgb(1,0,1))
abline(h=1/sqrt(2)^2,col=rgb(1,1,0))
#凡例
legend("bottomright", legend=c("Mj=2+Mn,Mn=√8/2","Mj=√2+Mn,Mn=(2-√2)/2","Mj=1+Mn,Mn=(√2-1)/2","Mj=√2/2+Mn,Mn=(1-√2/2)/2","Mj=1/2+Mn,Mn=(√2/2-1/2)/2"), lty=c(1,1,1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1),rgb(1,0,1),rgb(1,1,0)))

統計言語Rによる「サンプリング結果のマッピング」
R_time=seq(0,2*pi,length=400)
Smp_time=seq(0,pi/2,length=100)#標準円(半径1→sqrt(2))
f0<-function(x){cos(x)+cos(x-pi/2)}
S_data<-c(f0(Smp_time),f0(Smp_time),f0(Smp_time),f0(Smp_time))
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,2),main="Torus drawn by circumscribed and inscribed circle",ylab='Circumference(radian)', xlab='Circle radius')
#半径sqrt(2)→2
par(new=T) #上書き
S_data<-c(f0(Smp_time)*sqrt(2),f0(Smp_time)*sqrt(2),f0(Smp_time)*sqrt(2),f0(Smp_time)*sqrt(2))
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,2),ylab='', xlab='')#半径1→1/sqrt(2)
par(new=T) #上書き
S_data<-c(f0(Smp_time)/sqrt(2),f0(Smp_time)/sqrt(2),f0(Smp_time)/sqrt(2),f0(Smp_time)/sqrt(2))
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,2),ylab='', xlab='')#半径1/sqrt(2)→1/2
par(new=T) #上書き
S_data<-c(f0(Smp_time)/sqrt(2)^2,f0(Smp_time)/sqrt(2)^2,f0(Smp_time)/sqrt(2)^2,f0(Smp_time)/sqrt(2)^2)
plot(R_time,S_data,type="l",xlim=c(0,2*pi),ylim=c(0.5,2),ylab='', xlab='')
#外接円=内接円による境界線
abline(h=2,col=rgb(1,0,0))
abline(h=sqrt(2),col=rgb(0,1,0))
abline(h=1,col=rgb(0,0,1))
abline(h=1/sqrt(2),col=rgb(1,0,1))
abline(h=1/sqrt(2)^2,col=rgb(1,1,0))
#凡例
legend("bottomright", legend=c("Mj=2+Mn,Mn=√8/2","Mj=√2+Mn,Mn=(2-√2)/2","Mj=1+Mn,Mn=(√2-1)/2","Mj=√2/2+Mn,Mn=(1-√2/2)/2","Mj=1/2+Mn,Mn=(√2/2-1/2)/2"), lty=c(1,1,1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1),rgb(1,0,1),rgb(1,1,0)))
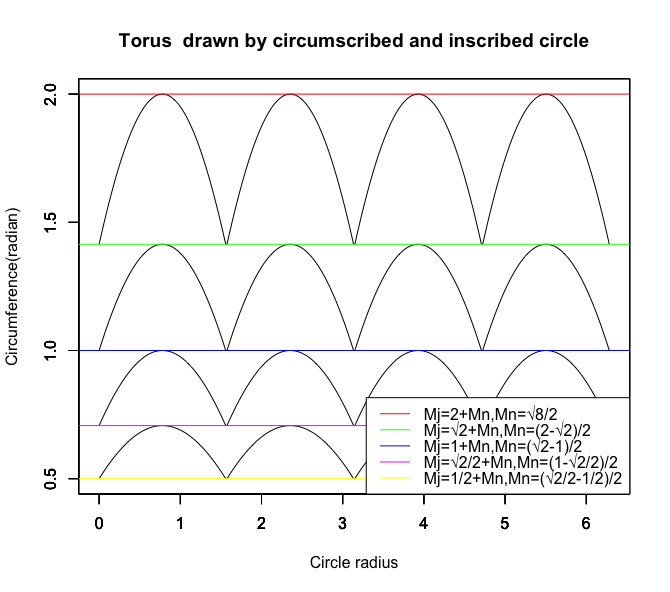
また位相のズレが90度(1/2πラジアン)単位なのでSin(θ)波が直交して円を描く。
*ただし「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」の制約で1/4のみ。これを4回繰り返す。
④正方形(Square)以上の多角形の場合


もはや「単層トーラス(Simplex Torus)」しか構築しない。
*より正確には「理論上それが構成されると考えるのは不可能でもないが、連鎖効果が見込めない為に普通は無視される」という感じかも。
◎ 正五角形(Regular pentagon)の場合



◎ 正六角形(Regular Hexagon)の場合


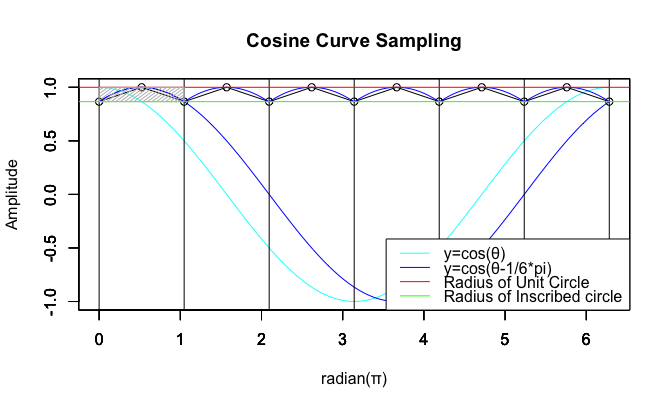
◎ 正七角形(Regular Heptago)の場合



◎ 正八角形(Regular Octagon)の場合



◎ 正九角形(Regular Pentagon))の場合


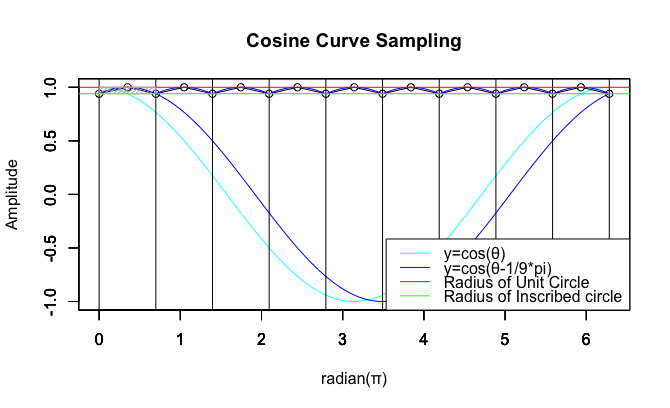
◎ 正十角形(Regular Decagon)の場合

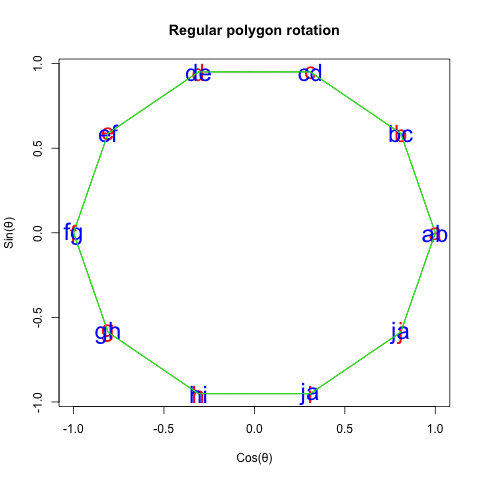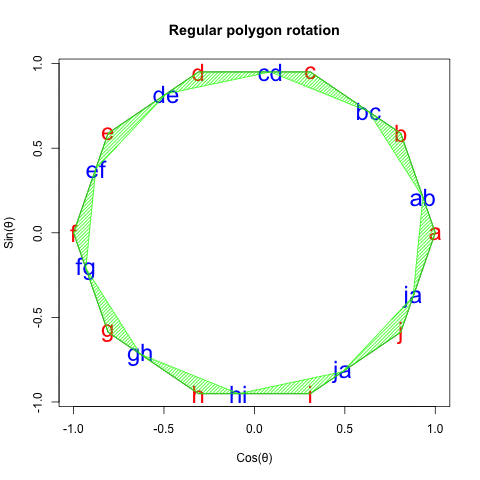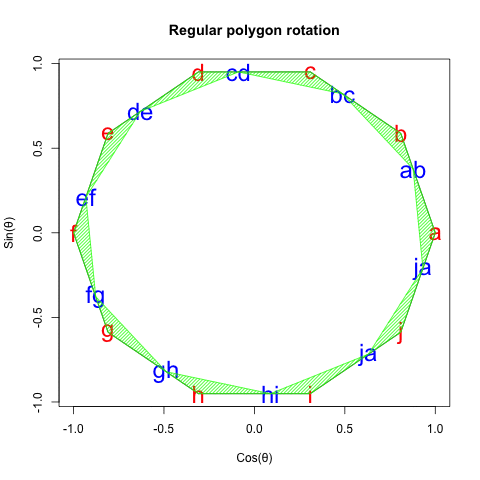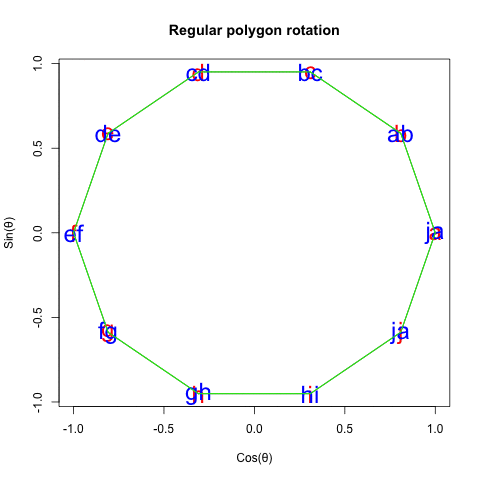

◎ 正11角形(Regular Hendecagon)の場合



◎ 正12角形(Regular Dodecagon)の場合



◎ 正16角形(Regular Hexagon)の場合


ちなみに以下はコーディング時参考にしたサイトのメモ。文字列処理、すぐに忘れちゃう…
*rep関数の使い方も、すぐに忘れちゃう…
*round関数の引数も、すぐに忘れちゃう…