正1角形(pi=3.141593ラジアンあるいは360度)の場合

平面上には描画可能な(あるいは立体との接点としてのみ映る)図形。概ね「球面上において出発点と終点を等しくする円周(距離も不定なら円面積全体)もしくは球表面(距離も不定なら球体積全体)」として想像される。その外接円の内接円に対する半径の比率は1倍、すなわち円周のそれと一致する。
「一角形は1つの辺と1つの内角しかもたないため、定義より全ての一角形は正一角形になる。」(wikipedia:一角形)
— κねこせん (@necocen) August 25, 2013
- 2*tan(pi)=-2.449294e-16
*これは「0に限りなく近い」という意味。 - 2*tan(pi)/cos(pi)=2.449294e-16
*符号にかかわらずこれも同様。 - cos(pi)=-1
ところで数学界には円周を2πでなく1τ(タウ)で表すべきとする立場もある。
角度をラジアン(弧度法)で表記したとき、「1周=τ」と表せるのが最大の利点である。
現在は高校の数学Ⅱで弧度法を学習するが、πが「半周」であることに違和感を覚えた人は多いだろう。
例えば、45°は1/8周なのに、πを使うと1/4πと表記しなければならない。τを使えば、1/8周は1/8τであり、直感的である。
実際のところどうなのだろう。とりあえず「どのタイミングで観測しても観測結果が必ず2π=1τとなる球面上の唯一の点(観測原点あるいは観測対象)が等速円運動している」と仮定してみる。
統計言語Rによるプログラミング例
#RH=1角形(Regular Henagon)
#Radian=角度(60分割)
RH<-function(Radian){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="l",main="Regular Henagon",xlab="cos(θ)",ylab="sin(θ)")
text(cx[Radian],cy[Radian],"X",col=rgb(1,0,0))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
RH(i)
}
}, interval = 0.1, movie.name = "RH01.gif")

普通に考えると球面上の対応する動きはこうなる。
統計言語Rによる作図
#正1角形
library(rgl)
Rtime<-seq(0,2,length=100)
tr01<-exp(seq(0,2*pi,length=100)*(0+1i))
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test100")
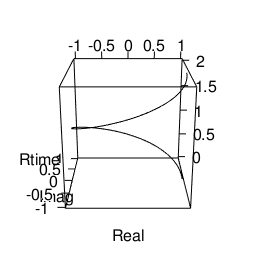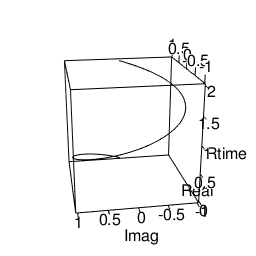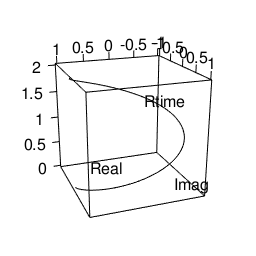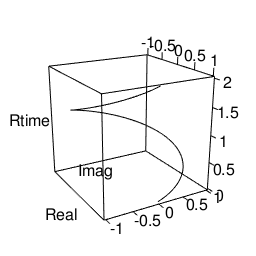

実際にはこういう動きをしてるかもしれない。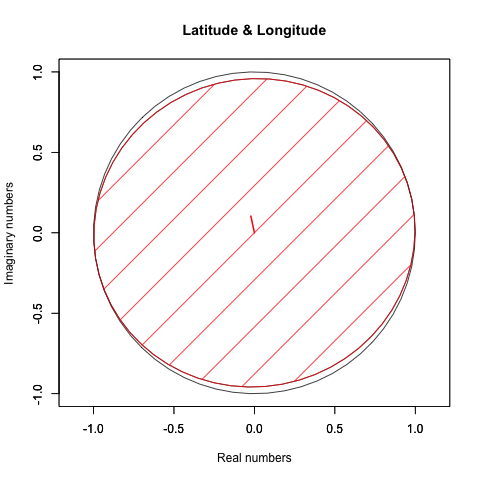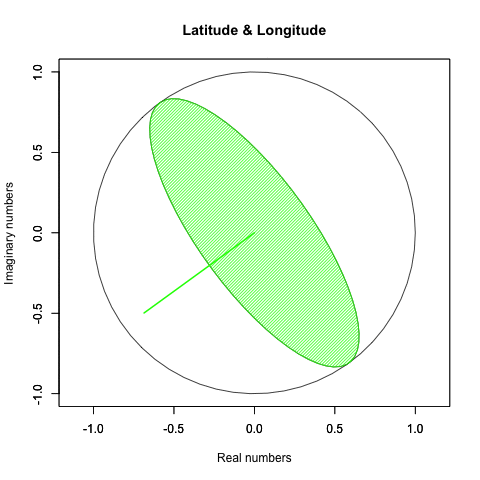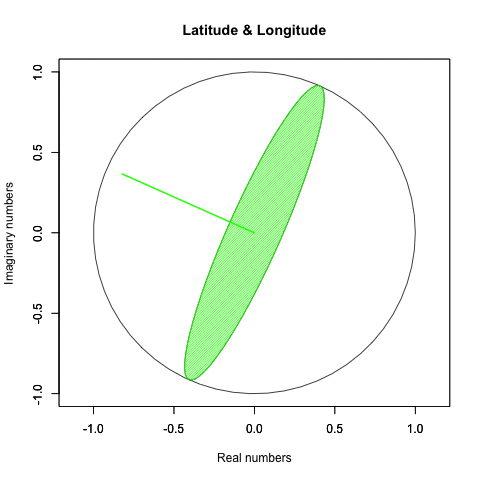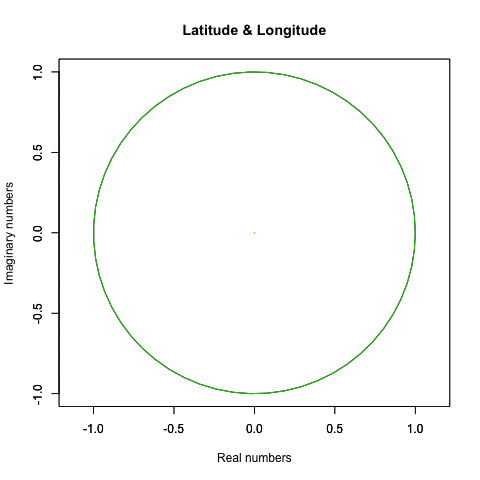
何れにせよそれを確かめる手段がないのである。むしろ「球面上の任意の位置に唯一の点(観測原点あるいは観測対象)が確率的に存在している」と捉えた方が状況を正確に要約してると言えるかもしれない。とりあえず「多角形におけるコサイン波サンプリング効果(Cosine wave sampling effect in polygons)」に基づく諸元は以下となる。
- 単位円(Unit Circle, 半径1の円弧)上においては辺数=1、辺長(2π/辺数)=2πあるいは1τ。球面上にのみ描画可能。
- 「サンプリング」元波形はcos(θ-π)=-cos(θ)でサンプリング範囲が0からπに及ぶので繰り返されない。オリジナル波形cos(θ)と合成すると完全に打ち消しあって水平化(Flatline)する。
統計言語Rによるプログラミング例。
cx<-seq(0,2*pi,length=60)
cy1<-cos(c0)*-1
plot(cx,cy1,type="l",main="Trajectory of Regular Henagon",xlab="Radians",ylab="Amplitude")par(new=T) #上書き
cy2<-cos(cx)
plot(cx,cy2,type="l",col=rgb(0,0,1),main="",xlab="",ylab="")
par(new=T) #上書き
cy3<-cos(cx)-cos(cx)
plot(cx,cy3,type="l",col=rgb(1,0,0),main="",xlab="",ylab="")
#凡例
legend("bottomright", legend=c("Sampling_wave=-cos(θ)","Origin_wave=cos(θ)","Sampling_wave+Origin_wave"), lty=c(1,1,1), col=c(rgb(0,0,0),rgb(0,0,1),rgb(1,0,0)))
もちろんCos(θ)波と-Cos(θ)波を直交させても、それ単体ではあまり面白い観測結果とはなり得ない。
統計言語Rによるプログラミング例。
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)*-1
plot(cx,cy,type="o",main="Cos(θ) orthogonal -Cos(θ) ",xlab="cos(θ)",ylab="-cos(θ)")
#凡例
legend("bottomright", legend=c("cos(θ) orthogonal -cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))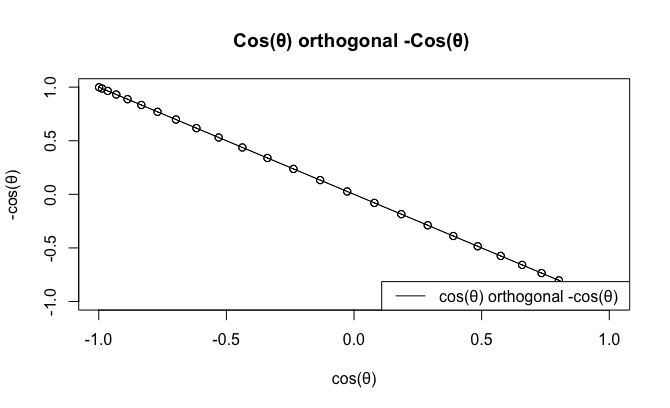
- あらゆる観測結果が水平化(Flatline)する為、サンプリング波形の頂点は計測不能、その値は全て外接円の半径(単位円の場合は1)そのものとなる。
位相幾何学(Topology)的にトーラス(単数形torus, 複数形tori)形状と看做す時は、概ね円そのもの(Circle itself)の特徴の真逆が割り振られる。
また、こんな特徴も指摘されている。
- 大円を2π回る間に小円を-2回って原点に戻る。
- 逆方向に進んでも同じ結果となる。
とにかく観測結果に従って認識論的に時空間イメージを構築する事が不可能なのが最大の特徴であり、もう一つの極限状態たる円そのもの(Circle itself)との(認識の対象範囲外における)連続性を想定するケースすら存在します。