まずは基本中の基本、すなわち「正弦波の位相変遷の法則」の確認から入りましょう。


この様にサイン波はコサイン波と位相が-90度ズレています。
サイン波(正弦波、sine wave、sinusoidal wave) - Wikipedia
正弦関数として観測可能な周期的変化を示す波動のことで、その波形は正弦曲線(sine curve)もしくはシヌソイド (Sinusoid) と呼ばれ、数学、信号処理、電気工学およびその他の分野において重要な働きをする。
コサイン波形(余弦波)もシヌソイドと言われる。これは、正弦波が後方にシフトされたもので波形が同一(Sin(θ+π/2)=Cos(θ))だからである。
統計言語Rによる検証結果。
Waves01<-function(prm){
#関数定義
f0=function(x) cos(x)
f1=function(x) sin(x)
f2=function(x) -sin(x)
f3=function(x) cos(x+prm)
f4=function(x) cos(x-prm)
#正弦波描写plot(f0,type="l",xlim=c(-pi,pi),ylim=c(-1,1),main="cos(x+pi/2)=-sin(x), cos(x-pi/2)=sin(x)",xlab="Frequency",ylab="Amplitude")
par(new=T) #上書き指定
plot(f1,type="l",xlim=c(-pi,pi),col=rgb(1,1,0),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f2,type="l",xlim=c(-pi,pi),col=rgb(0,1,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f3,type="l",xlim=c(-pi,pi),col=rgb(0,0,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f4,type="l",xlim=c(-pi,pi),col=rgb(1,0,0),ylim=c(-1,1),main="",xlab="",ylab="")#凡例
legend("bottomleft", legend=c("Cos(θ)","Sin(θ)","-Sin(θ)","Cos(θ+π/x)","Cos(θ-π/x)"), lty=c(1,1,1,1,1), col=c(rgb(0,0,0),rgb(1,1,0),rgb(0,1,1),rgb(0,0,1),rgb(1,0,0)))
}library("animation")
Time_Code=seq(0,pi/2,length=15)
saveGIF({
for (i in Time_Code){
Waves01(i)
}
}, interval = 0.1, movie.name = "CosSin01.gif")

統計言語Rによる検証結果。
Waves02<-function(prm){
#関数定義
f0=function(x) cos(x)
f1=function(x) -cos(x)
f2=function(x) cos(x+prm)
f3=function(x) cos(x-prm)
#正弦波描写plot(f0,type="l",xlim=c(-pi,pi),ylim=c(-1,1),main="cos(x+pi)=cos(x-pi)=-cos(x)",xlab="Frequency",ylab="Amplitude")
par(new=T) #上書き指定
plot(f1,type="l",xlim=c(-pi,pi),col=rgb(1,0,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f2,type="l",xlim=c(-pi,pi),col=rgb(0,0,1),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T) #上書き指定
plot(f3,type="l",xlim=c(-pi,pi),col=rgb(1,0,0),ylim=c(-1,1),main="",xlab="",ylab="")#凡例
legend("bottomleft", legend=c("Cos(θ)","-Cos(θ)","Cos(θ+π/x)","Cos(θ-π/x)"), lty=c(1,1,1,1), col=c(rgb(0,0,0),rgb(1,0,1),rgb(0,0,1),rgb(1,0,0)))
}library("animation")
Time_Code=seq(0,pi,length=15)
saveGIF({
for (i in Time_Code){
Waves02(i)
}
}, interval = 0.1, movie.name = "CosCos01.gif")

ちなみに統計言語Rから呼び出せる汎用代数ライブラリRyhacasは、こういう「頭が悪く見えそうな」単純過ぎる位相変遷を扱ってくれません。単なる計算機のくせにお高くとまりやがって…
統計言語R with 汎用代数ライブラリRyacasによる検証結果。
library(Ryacas)
#Cos(x+Pi/2)yac("Cos(x+Pi/2)")
[1] "Cos(x+Pi/2)"
yac("TrigSimpCombine(Cos(x+Pi/2))")
[1] "Cos(Pi/2+x)"#Cos(x-Pi/2)
yac("Cos(x-Pi/2)")
[1] "Cos(x-Pi/2)"
yac("TrigSimpCombine(Cos(x-Pi/2))")
[1] "Cos(Pi/2-x)"#Cos(x+Pi)
yac("Cos(x+Pi)")
[1] "Cos(x+Pi)"
yac("TrigSimpCombine(Cos(x+Pi))")
[1] "Cos(Pi+x)"
#Cos(x-Pi)
yac("Cos(x-Pi)")
[1] "Cos(x-Pi)"
yac("TrigSimpCombine(Cos(x-Pi))")
[1] "Cos(Pi-x)"
実質ここでやってるのは三角関数の微積分そのもので、そういう「頭が良く見えそうな」の問題なら解いてくれます。
解析学の基本的な部分を形成する数学の分野の一つである。局所的な変化を捉える微分と局所的な量の大域的な集積を扱う積分の二本の柱からなり、分野としての範囲を確定するのは難しいが、大体多変数実数値関数の微分と積分に関わる事柄(逆関数定理やベクトル解析も)を含んでいる。
- 微分(Derivative)…ある関数のある点での接線、あるいは接平面を考える演算である。数学的に別の言い方をすると、基本的には複雑な関数を線型近似して捉えようとする考え方である。従って、微分は線型写像になる。但し、多変数関数の微分を線型写像として捉える考え方は 20世紀に入ってからのものである。微分方程式はこの考え方の自然な延長にある。
- 積分(Integrate)…幾何学的には、曲線、あるいは曲面と座標軸とに挟まれた領域の面積(体積)を求めることに相当している。ベルンハルト・リーマンは(一変数の)定積分の値を、長方形近似の極限として直接的に定義し、連続関数は積分を有することなどを証明した。彼の定義による積分をリーマン積分と呼んでいる。
微分と積分はまったく別の概念でありながら密接な関連性を持ち、一変数の場合、互いに他の逆演算としての意味を持っている(微分積分学の基本定理)。微分は傾き、積分は面積を表す。
①解析学(Mathematical Analysis)は正弦波を以下の様に捉える。
- Cos(θ)を微分すると-Sin(θ)となる(位相+90度)。
- Cos(θ)を積分するとSin(θ)となる(位相-90度)。
- Sin(θ)を微分するとCos(θ)となる(位相+90度)。
- Sin(θ)を微分すると-Cos(θ)となる(位相+90度)。
- Cos(θ)を2階微分すると-Cos(θ)となる(位相+180度)。
- Cos(θ)を2階積分すると-Cos(θ)となる(位相-180度)。
単なる計算機のくせにお高くとまりやがって…
統計言語R with 汎用代数ライブラリRyacasによる検証結果。
library(Ryacas)
#Cos(θ)を微分すると-Sin(θ)となる(位相-90度)。
yac("D(x) Cos(x)")
[1] "-Sin(x)"
#Sin(θ)を微分するとCos(θ)となる(位相-90度)。
yac("D(x) Sin(x)")
[1] "Cos(x)"
#Cos(θ)を積分するとSin(θ)となる(位相+90度)。
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"#Sin(θ)を微分すると-Cos(θ)となる(位相+90度)。
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
#Cos(θ)を2階微分すると-Cos(θ)となる(位相+180度)。
yac("D(x,2) Cos(x)")
[1] "-Cos(x)"#Cos(θ)を2階積分すると-Cos(θ)となる(位相-180度)。
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
- Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)→Cos(θ)
- Sin(θ)→Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)
- Cos(θ)→Sin(θ)→-Cos(θ)→-Sin(θ)→Cos(θ)
- Sin(θ)→-Cos(θ)→-Sin(θ)→Cos(θ)→Sin(θ)
統計言語R with 汎用代数ライブラリRyacasによる検証結果。
#Cos波の微分(位相変遷-90度、4回で1周)
yac("D(x,1) Cos(x)")
[1] "-Sin(x)"
yac("D(x,2) Cos(x)")
[1] "-Cos(x)"
yac("D(x,3) Cos(x)")
[1]"Sin(x)"
yac("D(x,4) Cos(x)")
[1] "Cos(x)"#Sin波の微分(位相変遷-90度、4回で1周)
yac("D(x,1) Sin(x)")
[1] "Cos(x)"
yac("D(x,2) Sin(x)")
[1] "-Sin(x)"
yac("D(x,3) Sin(x)")
[1] "-Cos(x)"
yac("D(x,4) Sin(x)")
[1] "Sin(x)"#Cos波の積分(位相変遷+90度、4回で1周)
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
yac("Integrate(x) -Cos(x)")
[1] "-Sin(x)"
yac("Integrate(x) -Sin(x)")
[1] "Cos(x)"#Sin波の積分(位相変遷+90度、4回で1周)
yac("Integrate(x) Sin(x)")
[1] "-Cos(x)"
yac("Integrate(x) -Cos(x)")
[1] "-Sin(x)"
yac("Integrate(x) -Sin(x)")
[1] "Cos(x)"
yac("Integrate(x) Cos(x)")
[1] "Sin(x)"
③この性質は指数関数(Exponential function)や対数関数(Logarithm function)と似てるのでセットで扱われる事が多い。
指数関数内における±90度位相変遷
- -90度(微分)方向…exp(θ)→-exp(-θ)→-exp(-θ)→exp(-θ)→exp(θ)
- +90度(積分)方向…exp(θ)→exp(-θ)→-exp(-θ)→-exp(θ)→exp(θ)
対数関数内における±90度位相変遷
指数・対数関数間変遷を含む±90度位相変遷
指数関数
対数関数
悲しい事に統計言語Rから呼び出せる汎用代数ライブラリRyhacasは(というより解析学そのものが)こういう「頭が悪く見えそうな」時代遅れの位相変遷を扱ってくれません。単なる計算機のくせにお高くとまりやがって…一方、こうやって三角関数と対数・指数関数の関係をまとめて扱えると何が嬉しいって、テイラー級数(Taylor series)/マクローリン級数(Maclaurin series)を用いて三角関数や指数・対数関数の計算結果に近似値が与えられる様になるのです。こうした定理が出揃った18世紀には航海の世界も建築の世界もこうした近似値一覧表に頼ってましたから、かかる諸概念の整理は驚くべきパラダイムシフトを産んだのでした。
Cos(θ)波の近似値算出過程
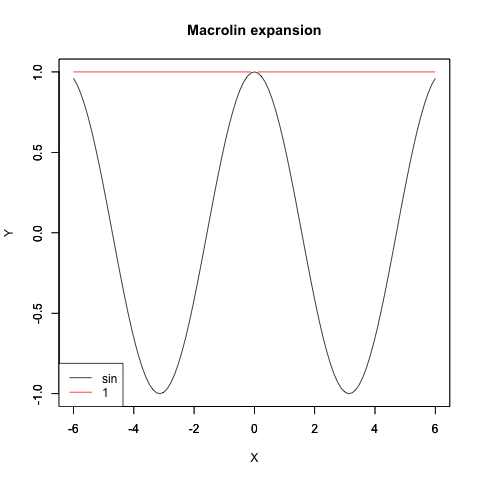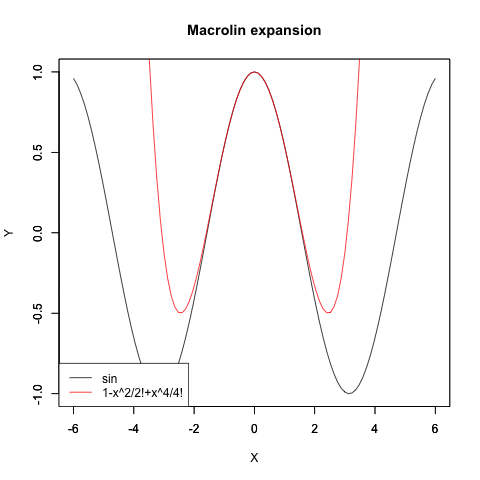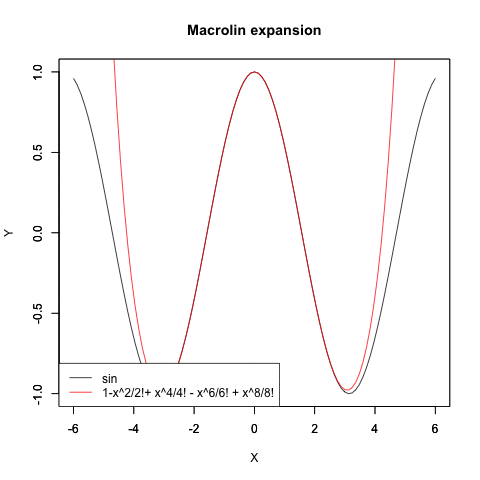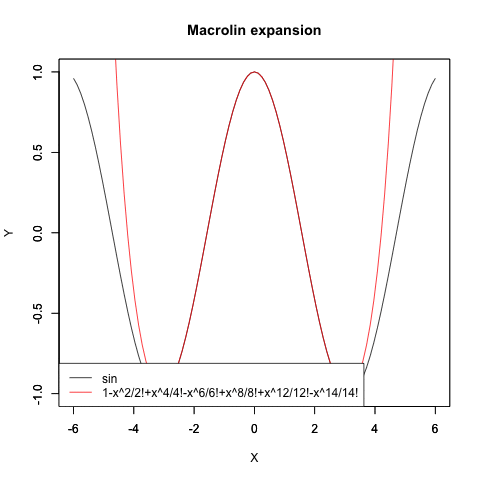
Sin(θ)波の近似値算出過程
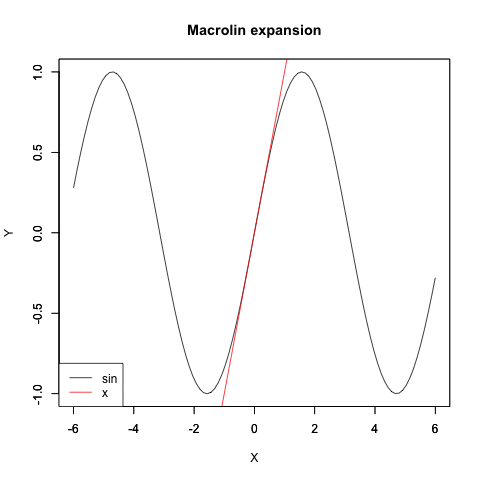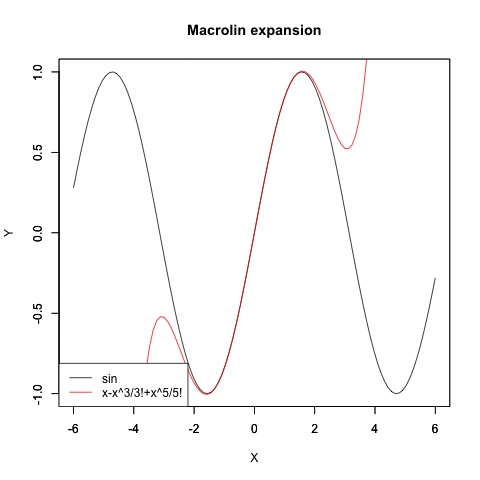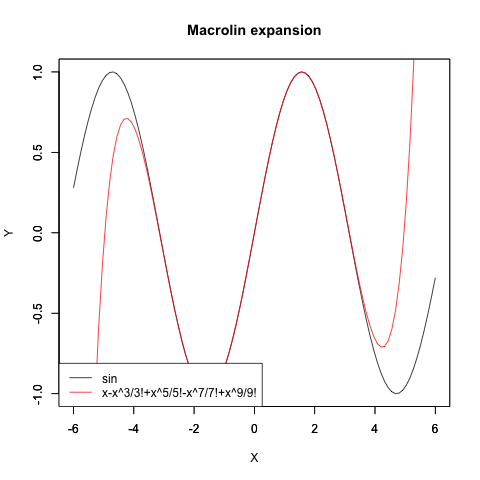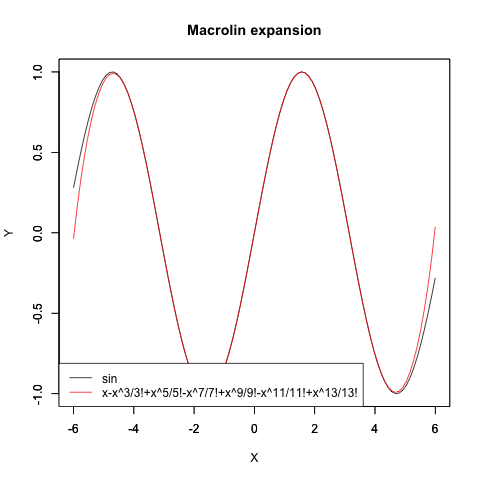
指数関数e^xの近似値算出過程
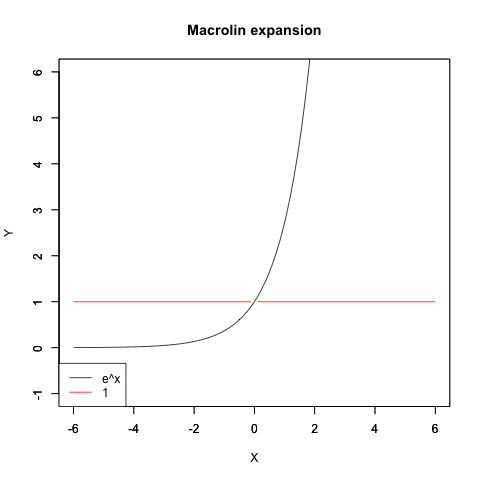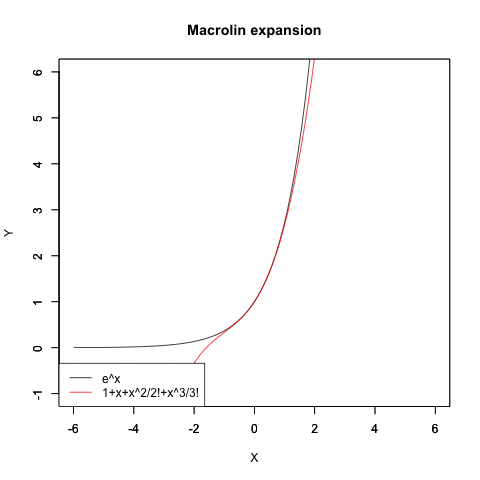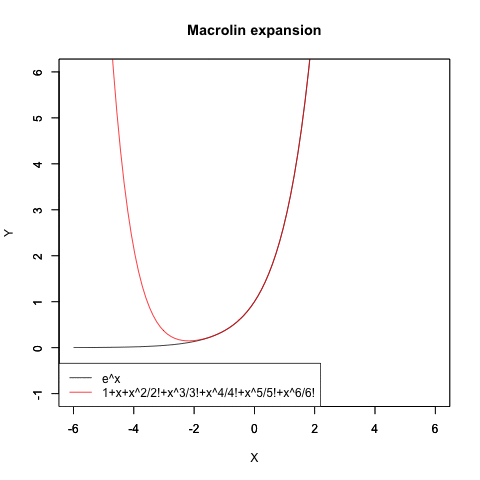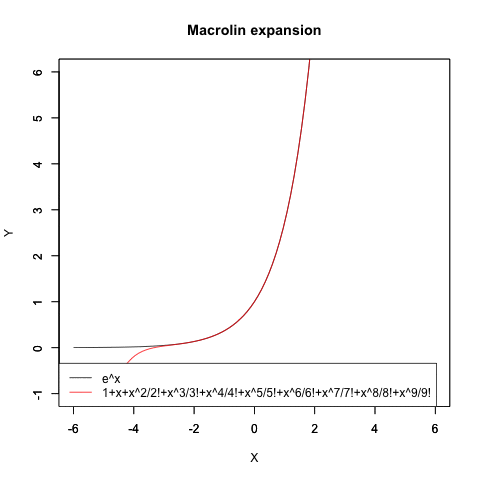
オイラーの公式(Euler's formula)e^π-θi=cos(θ)+sin(θi)がこうした検討を下敷きに生まれたのは有名な話ですが、実は当時はまだ複素数平面/ガウス平面(独Zahlenebene/Komplexe Zahlenebene、英complex plane、Gaussian plane)の概念が十分に確立していなかったせいで、複素数(Complex Number)概念も小数点を含まない自然数(Natural Number、小数点を含まない0,1,2,3…Nなる体裁の数列)の形でしか扱えず、そうした離散的アプローチではちゃんと円が描けない事も当時の数学者達の認識対象外となったのです。
複素平面(独Zahlenebene/Komplexe Zahlenebene、英complex plane、Gaussian plane) - Wikipedia
x, yが実数であるとき、複素数x + iyを単に実数の対とみなせば、平面の直交座標 (x, y) の点に対応付けることができる。xy-平面上の y-軸は純虚数の全体に対応し、虚軸 (imaginary axis) と呼ばれる。xy-平面上の点 (x, y) に複素数z=x + iyを対応させるとき、z-平面とも言う。
1811年頃にガウスによって導入されたため、ガウス平面 (Gaussian plane) とも呼ばれる。一方、それに先立つ1806年に Jean-Robert Argandも同様の手法を用いたている為、アルガン図 (Argand Diagram)とも呼ばれている。さらに、それ以前の1797年の Caspar Wesselの書簡にも登場している。このように複素数の幾何的表示はガウス以前にも知られていたが、今日用いられているような形式で複素平面を論じたのはガウスである。三者の名前をとってガウス・アルガン平面、ガウス・ウェッセル平面などとも言われる。
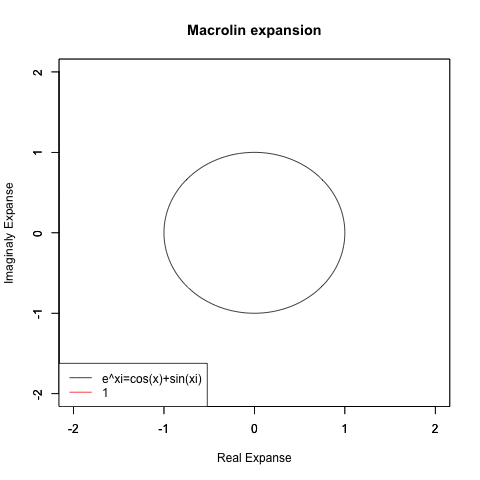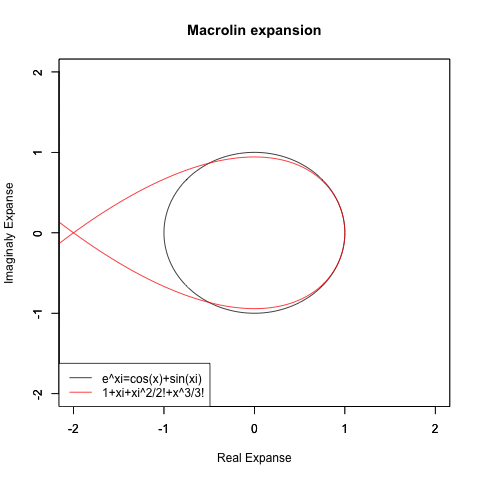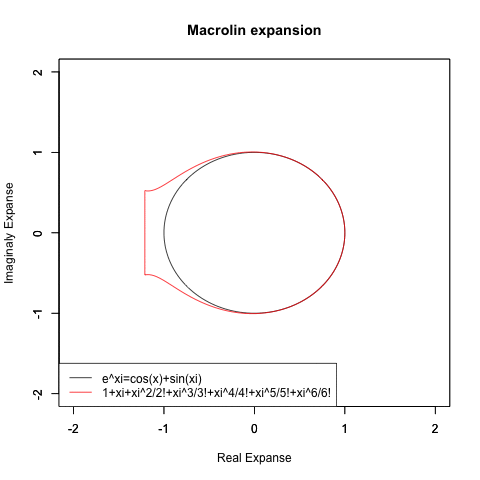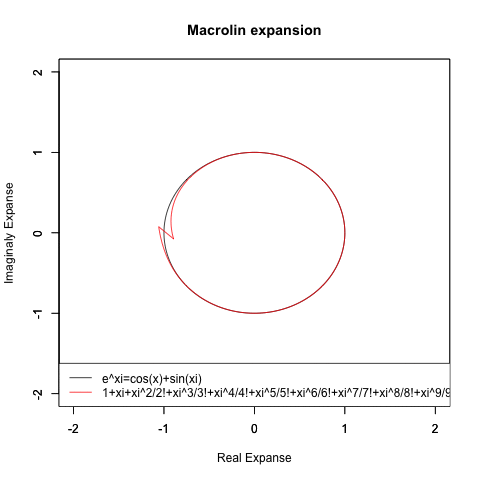
ここで下手に躓かなかった事はある意味、人類史にとって幸いだったとも?

いずれにせよオイラーの公式(Euler's formula)e^π-θi=cos(θ)+sin(θi)も複素数平面/ガウス平面(独Zahlenebene/Komplexe Zahlenebene、英complex plane、Gaussian plane)の概念も成立して以降の数学史は不可逆的にアイザック・ニュートン(Sir Isaac Newton、1642年〜1727年)やゴットフリート・ライプニッツ(Gottfried Wilhelm Leibniz、1646年〜1716年)が切り拓いた近世段階を抜け、実数(Real Number)と虚数(Imaginary number)の(複素数平面上における)連続が当然視される近代段階へと足を踏み入れる事になったのでした。