①外接円に対する内接円の半径の比率はCos(π/n)で推移し、究極的には円のそれ、すなわち1倍(Cos(0))と合致する。
統計言語Rによる実証例
#cos(pi/x)の振る舞い
f0=function(x) cos(pi/x)
plot(f0,xlim=c(0,50),ylim=c(-1,1),main="Ratio of inscribed circle and circumscribed circle",xlab="x(Number of vertices)",ylab="cos(pi/x)")

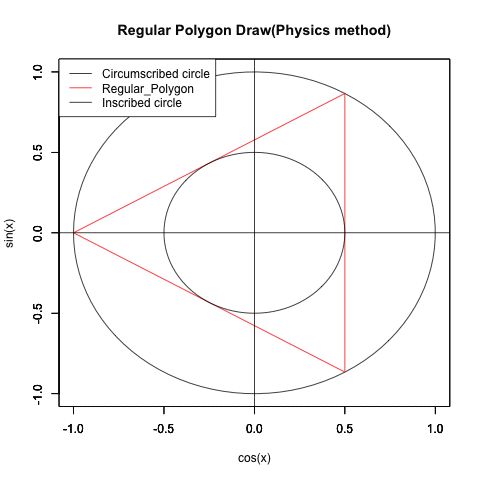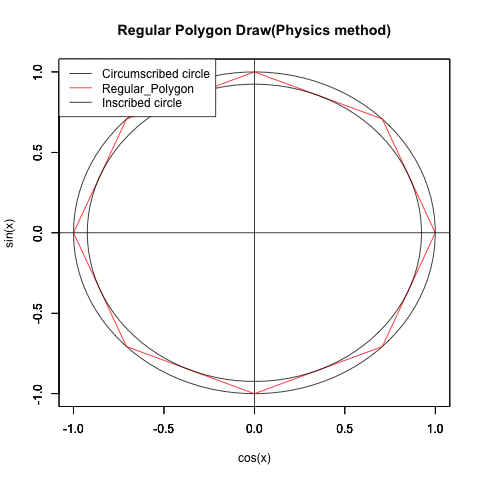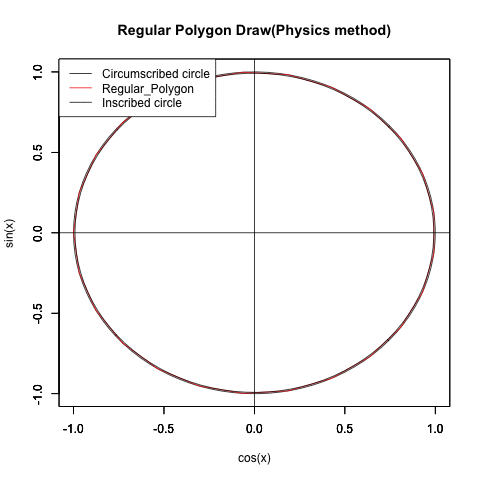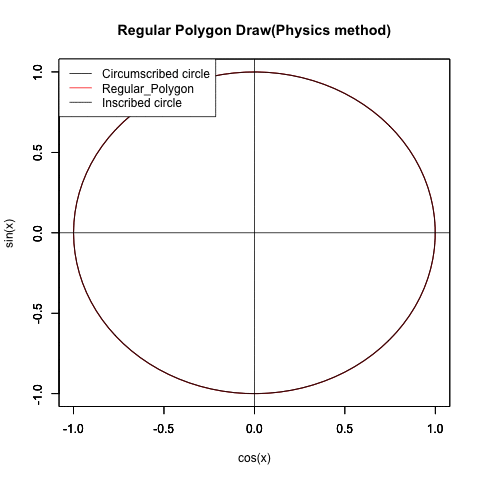
②この過程を外接円と内接円に挟まれた正多角形の側から見るとこうなる。
統計言語Rによる実習(等速円運動の写像を使う物理スタンス)
Regular_Polygon_draw01<-function(x) {
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"#タイトル定義
Main_title<-c("Regular Polygon Draw(Physics method)")
x_title<-c("cos(x)")
y_title<-c("sin(x)")#グラフのスケール決定
gs_x<-c(-1,1)
gs_y<-c(-1,1)
#y=sin(x)
f1_name<-c("Circumscribed circle")
c0<-seq(-pi,pi,length=100)
#y=2*sin(x)
f2_name<-c("Regular_Polygon")
c1<-seq(-pi,pi,length=x+1)
#y=3*sin(x)
f3_name<-c("Inscribed circle")
scl<-cos(pi/x)
#グラフ描画
plot(cos(c0),sin(c0),xlim=gs_x,ylim=gs_y,type="l",col=Black, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(cos(c1),sin(c1),xlim=gs_x,ylim=gs_y,type="l",col=Red, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(cos(c0)*scl,sin(c0)*scl,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
#基準線
abline(h=0)
abline(v=0)
#凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Black,Red,Black))
}library("animation")
Time_Code=c(3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,11,12,13,14,15,20,25,30,35,40,45,50,60,70,80,90,100)
saveGIF({
for (i in Time_Code){
Regular_Polygon_draw01(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
統計言語Rによる実習(複素係数を自然指数・対数関数に適用した数理スタンス)
Regular_Polygon_draw02<-function(x) {
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"#タイトル定義
Main_title<-c("Regular Polygon Draw(
Mathematical method)")
x_title<-c("Real number")
y_title<-c("Imaginary number")#グラフのスケール決定
gs_x<-c(-1,1)
gs_y<-c(-1,1)
#Circumscribed circle(外接円)
f1_name<-c("Circumscribed circle")
f0<-function(x){exp(x*(0+1i))}
c1<-seq(-pi,pi,length=100)
c1_r<-Re(f0(c1))
c1_i<-Im(f0(c1))
#Regular_Polygon(正多角形)
f2_name<-c("Regular_Polygon")
c2<-seq(-pi,pi,length=x+1)
c2_r<-Re(f0(c2))
c2_i<-Im(f0(c2))
#Inscribed circle(内接円)
f3_name<-c("Inscribed circle")
scl<-cos(pi/x)
#グラフ描画
plot(c1_r,c1_i,xlim=gs_x,ylim=gs_y,type="l",col=Black, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(c2_r,c2_i,xlim=gs_x,ylim=gs_y,type="l",col=Red, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(c1_r*scl,c1_i*scl,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
#基準線
abline(h=0)
abline(v=0)
#凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Black,Red,Black))
}
library("animation")
Time_Code=c(3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,11,12,13,14,15,20,25,30,35,40,45,50,60,70,80,90,100)
saveGIF({
for (i in Time_Code){
Regular_Polygon_draw02(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
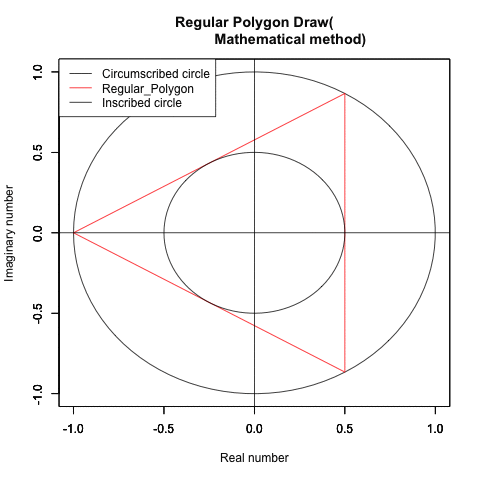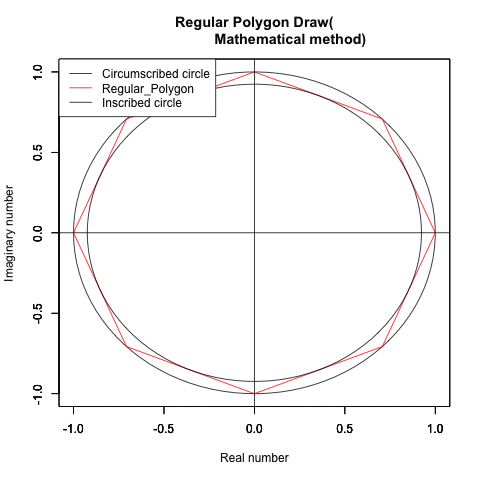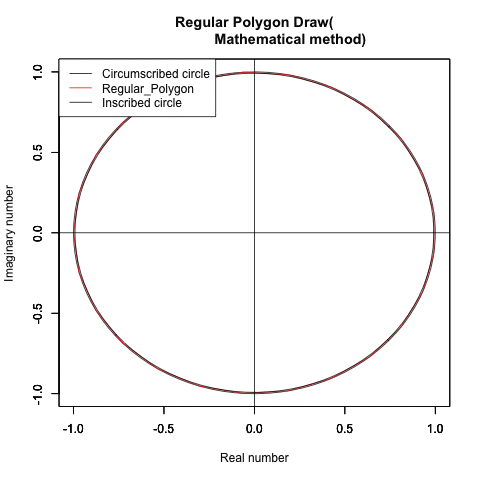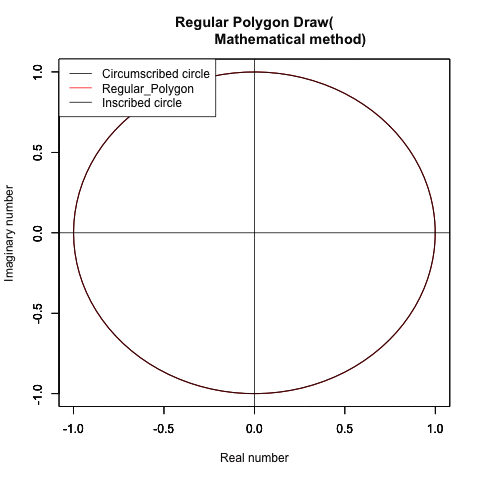
実は線積分(line integral, path integral=経路積分)∫(-π,π,sqrt(-sin(θ))+cos(θ))dt)になってる?
統計言語Rによる実習(基本円(半径1の円周)に対する内接多角形と外接多角形の辺長合計の極限としての2π)
Regular_Polygon_draw03<-function(x) {
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"#タイトル定義
Main_title<-c("The Limit of inscribed polygons and circumscribed polygons")
x_title<-c("Real number")
y_title<-c("Imaginary number")#グラフのスケール決定
gs_x<-c(-1,1)
gs_y<-c(-1,1)
#Circumscribed circle(外接多角形)
f1_name<-c("Circumscribed Polygon")
f0<-function(x){exp(x*(0+1i))}
c1<-seq(-pi,pi,length=x+1)
c1_r<-Re(f0(c1))
c1_i<-Im(f0(c1))
#Regular_Polygon(中間円)
f2_name<-c("Inner circle")
c2<-seq(-pi,pi,length=100)
c2_r<-Re(f0(c2))
c2_i<-Im(f0(c2))
#Inscribed circle(内接多角形)
f3_name<-c("Inscribed Polygon")
scl<-cos(pi/x)
#グラフ描画
plot(c1_r,c1_i,xlim=gs_x,ylim=gs_y,type="l",col=Green, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(c2_r*scl,c2_i*scl,xlim=gs_x,ylim=gs_y,type="l",col=Black, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(c1_r*scl,c1_i*scl,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
#基準線
abline(h=0)
abline(v=0)
#凡例描画
legend("topleft", legend=c(f1_name,f2_name,f3_name),lty=c(1,1,1),col=c(Green,Black,Blue))
}
library("animation")
Time_Code=c(3,3,4,4,5,5,6,6,7,7,8,8,9,9,10,11,12,13,14,15,20,25,30,35,40,45,50,60,70,80,90,100)
saveGIF({
for (i in Time_Code){
Regular_Polygon_draw03(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

統計言語Rによる実習(基本円(半径1の円周)に対する内接多角形と外接多角形の辺長合計の極限としての2π)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"
#タイトル
Main_title<-c("The Limit of inscribed polygons and circumscribed polygons ")
x_title<-c("x")
y_title<-c("y")#x軸=多角形の範囲(3~100)
c0<-seq(3,100,length=98)
#グラフのスケール決定
gs_x<-c(3,60)
gs_y<-c(5,10.5)
#基準円に外接する正多角形
f1_name<-c("Circumscribed Regular Polygons")
Circumscribed_Regular_Polygons_all_around<-function(n) {(2*tan(pi/n))*n}
c1<-Circumscribed_Regular_Polygons_all_around(c0)
#基準円に内接する正多角形
f2_name<-c("Inscribed Regular Polygons")
Inscribed_Regular_Polygons_all_around<-function(n) {(2*tan(pi/n))*cos(pi/n)*n}
c2<-Inscribed_Regular_Polygons_all_around(c0)
#描画
plot(c0,c1,xlim=gs_x,ylim=gs_y,type="l",col=Green, main=Main_title,xlab=x_title,ylab=y_title)par(new=T)#上書き指定
plot(c0,c2,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")abline(h=pi*2)
legend("topright", legend=c(f1_name,f2_name,"y=2π"),lty=c(1,1,1),col=c(Green,Blue,Black))

ある意味これもヤコブ・ベルヌーイの「大数の弱法則 (WLLN: Weak Law of Large Numbers) 」すなわち「独立同分布/独立同一分布に従う可積分な確率変数の無限列X1, X2,…Xnとその平均μが与えられた時、標本平均(Sample mean)(X1, X2,…Xn)/n(ただしn>=1) のとる値が平均μの近傍から外れる確率は、十分大きなnを取れば、いくらでも小さくできる」なる概念の証明の一つとなってますね。
- 独立同分布/独立同一分布(independent and identically distributed; IID, i.i.d., iid)…確率論と統計学において、確率変数の列やその他の系が、それぞれの確率変数が他の確率変数と同じ確率分布を持ち、かつ、それぞれ互いに独立している場合をいう。例えば6面体サイコロで各出目の確率は毎回1/6であり、その前後の出目の影響を受けない(メモリレス性)。「独立同分布/独立同一分布」なる確率分布自体が存在する訳ではない点に注意。
-
可積分(integrable)…ニュートンが17世紀にケプラー問題を解いて微分積分学や古典力学が発祥して以降追求されてきた「求積法で完全に解ける」範囲。
例えば「物差しの目盛は収束などしてはいけない」ルールに従って指数・対数関数や三角関数を「収束しない基準」として採用したフーリエ解析(Fourier analysis)におけるフーリエ展開(Fourier expansion)/フーリエ逆展開(Fourier inverse expansion)は、その立ち場故に指数・対数関数や三角関数そのものを直接扱えない(決して収束しないからこそ正負の目盛りが無限に続き微積分演算の対象となり得ない)。あえてこの制約を破ろうとしたのがラプラス変換となる。
- 確率変数(random variable, aleatory variable, stochastic variable)…ある確率のセットが変数として存在し、しかも概ねそうした確率の合計が1となる様に正規化(normalization)された状態モデルを指す。例えばコインの出目は{表,裏}のいずれかで、それぞれの目が出る確率は1/2(P(X)=1/2(x=0,1))。6面体サイコロを投げて出る目は{1, 2, 3, 4, 5, 6}のいずれかで、それぞれの目が出る確率は1/6(P(X)=1/6(x=1,2,3,4,5,6))。3の目が出る確率は1/6(P(X=3)=1/6,P(3)=1/6)。

一般化するとP(X)=1/N(X=1,2,3…N)となり、ここから以下に述べるベルヌーイ過程(Bernoulli process)」(1-1/N)^N(各出目の出現確率が均等に1/NのN面体サイコロをN回降って特定の目が1回も出ない確率)も導出される。
要するに「角度2πラジアン」を「距離2π」に変換してるだけですが…考えてみれば後者はフーリエ逆変換やラプラス逆変換に通じる? ならば前者は?