
そもそも「フーリエ解析(Fourier analysis)」は、全ての波形について(Sin波やCos波の様な)正弦波に適正な数字を掛けて足し合わせたら再現可能と考えます。
なので微積分の分野同様に「既存の方法で取り零してきた例を、より高度なテクニックの導入により解析する」過程を積み重ねてきたのです。
*要するに「まともな関数」と「ヤバい関数」の峻別と克服のプロセス?
①-1.有限期間-T/2<=t<=T/2における「フーリエ級数展開」。これが出発点。
有限期間-T/2<=t<=T/2における「フーリエ級数展開」
- f(t)=a0+(a1*cos(2π*t/T)+b2*sin(2π*t/T))+(a2*cos(4π*t/T)+b1*sin(4π*t/T))+(a3*cos(6π*t/T)+b2*sin(6π*t/T))+…+(an*cos(2πn*t/T)+bn*sin(2πn*t/T))+…
- a0=1/T*∫(-T/2<=t<=T/2,f(t)dt)
- an=2/T*∫(-T/2<=t<=T/2,f(t)cos(2π*n*t/T)dt)
- bn=2/T*∫(-T/2<=t<=T/2,f(t)sin(2π*n*t/T)dt)
- ただしT=波長(wavelength=展開したい元信号の周期)とする。基本円の場合は円周と同じで2π。オイラーの等式(Euler's identity)e^πi=-1は観測原点の対蹠地点(直線距離で2,円周上の距離でπ)を繰り返しの極限と見るのでこうなる。
またnは自然数とする。
この様なフーリエ級数展開が可能である為にはフーリエ係数を求める積分計算が可能でなければならな図、その為の制約が最も厳しい状態。
「空間的に捉える波」と「時間的に捉える波」の関係おさらい
波動の空間的定義
- 波長λ(ラムダ)
- 波数k
- k=2π/λ あるいは1(τ)/λ
波動の時間的定義
- 周期T
- 周波数(振動数)υ(ウプシロン)
- υ=1/T
上記を踏まえた正弦波(cos(ω*t),sin(ω*t))の定義
周波数(振動数)υの単位はHz(ヘルツ。1秒間あたりの振動数)
角周波数ωの単位はrad/s(ラディアン/秒。1秒間あたりの回転角)
①-2.さらに式セット①-1において「ω0(Basic Angular frequency=基本角周波数)=2π/T」と置くと式全体はこうなる。
有限期間-T/2<=t<=T/2における「フーリエ級数展開」
- f(t)=a0+(a1*cos(ω0*t)+b1*sin(ω0*t))+(a2*cos(2*ω0*t)+b2*sin(2*ω0*t))+(a3*cos(3*ω0*t)+b2*sin(3*ω0*t))+…+(an*cos(n*ω0*t)+bn*sin(n*ω0*t))+…
- a0=1/T*∫(-T/2<=t<=T/2,f(t)dt)
- an=2/T*∫(-T/2<=t<=T/2,f(t)cos(n*ω0)dt)
- bn=2/T*∫(-T/2<=t<=T/2,f(t)sin(n*ω0)dt)
ただし「ω0(Basic Angular frequency=基本角周波数)=2π/T」。
- a0はf(t)の変動しない成分の大きさ。
- cos(n*ω0)やcos(n*ω0)の角周波数(Angular frequency)はn*ω0。
とにかく式から表面上無理数πが消えたのが重要とも。
①-3.さらに式セット①-2に三角関数の合成式a*cos(θ)+b*sin(θ)=sqrt(a^2+b^2)*cos(θ+α)を用いるとこうなる。
有限期間-T/2<=t<=T/2における「フーリエ級数展開」
- f(t)=a0+sqrt(a1^2+b1^2)*cos(ω0*t*α1)+sqrt(a2^2+b2^2)*cos(ω0*t*α2*2)+sqrt(a3^2+b3^2)*cos(ω0*t*α3*3)+sqrt(an^2+bn^2)*cos(ω0*t*αn*3)+…
- a0=1/T*∫(-T/2<=t<=T/2,f(t)dt)
- an=2/T*∫(-T/2<=t<=T/2,f(t)cos(n*ω0)dt)
- bn=2/T*∫(-T/2<=t<=T/2,f(t)sin(n*ω0)dt)
- ただし「ω0(Basic Angular frequency=基本角周波数)=2π/T」。
- a0はf(t)の変動しない成分の大きさ。
- cos(n*ω0)やcos(n*ω0)の角周波数(Angular frequency)はn*ω0。
ここでsqrt(a1^2+b1^2)~sqrt(an^2+bn^2)はそれぞれの成分(角周波数ω0)の振幅、α1~αnはそれぞれの成分(角周波数ω0)に対する相対角度(Cos(0)の値{1,0}と原点{0,0}を結ぶ基準線に対する角度)に対応。後者はある意味、相関係数の概念に関与してくる。
ある意味スペクトル(spectrum)概念の大源流? ただしまだ表面上離散状態にあり、角評価軸の直交の保証もない…だが本当に?
②-1.次は定義域がp<=t<p+Tの「フーリエ級数展開」について考えてみる。
有限期間p<=t<p+Tにおける「フーリエ級数展開」
- f(t)=a0+(a1*cos(2π*t/T)+b2*sin(2π*t/T))+(a2*cos(4π*t/T)+b1*sin(4π*t/T))+(a3*cos(6π*t/T)+b2*sin(6π*t/T))+…+(an*cos(2πn*t/T)+bn*sin(2πn*t/T))+…
- a0=1/T*∫(p<=t<p+T,f(t)dt)
- an=2/T*∫(p<=t<p+T,f(t)cos(2πn*t/T)dt)
- bn=2/T*∫(p<=t<p+T,f(t)sin(2πn*t/T)dt)
ただしnは自然数とする。
②-2.式セット①-2.も当然同様に拡張可能。
有限期間p<=t<p+Tにおける「フーリエ級数展開」
- f(t)=a0+(a1*cos(ω0*t)+b1*sin(ω0*t))+(a2*cos(2*ω0*t)+b2*sin(2*ω0*t))+(a3*cos(3*ω0*t)+b2*sin(3*ω0*t))+…+(an*cos(n*ω0*t)+bn*sin(n*ω0*t))+…
- a0=1/T*∫(p<=t<p+T,f(t)dt)
- an=2/T*∫(p<=t<p+T,f(t)cos(n*ω0)dt)
- bn=2/T*∫(p<=t<p+T,f(t)sin(n*ω0)dt)
ところである周期Tが存在し、任意のtについてf(t+T)=f(t)が成立する時、関数f(t)を周期Tの周期函数という。記述をfs(t)と改める事もある。フーリエ級数によってこの状態をも記述する事を「周期的拡張(Periodic expansion)」という。
周期的拡張(Periodic expansion)にまつわる諸概念
不連続点におけるフーリエ級数の値…有限期間p<=t<p+Tで定義された関数f(t)に周期Tで周期的拡張を施した関数fs(t)はp+Tの箇所で不連続となる事がある。この時のフーリエ級数の値は丁度真ん中(中点)となる。
開区間の積分…数学では両端が入る区間を「閉区間(Closed section)」、両方とも入らない区間を「開区間(Open section)」、どちらか一方が入らない区間を「半開区間(Half-open section)」という。半開区間の積分では「lim(ε→+0)∫(a,b-ε,f(t)dx)が存在するなら、f(t)は閉区間[a,b)で積分可能である」と考え、この極限値を∫(a,b,f(t)dt)と表す。ここで記号ε→+0は正の値を取りながら0に限りなく近く事を意味する。
③ところで偶関数の「フーリエ余弦級数(Fourier cosine series)」と奇関数の「フーリエ正弦級数(Fourier sine series)」は同時出現しない。
関数f(x)が偶関数ならb0=0となり、以下の縦軸対称の波形となる(フーリエ余弦級数)。
- f(t)=a0+a1*cos(2π*t/T)+a2*cos(4π*t/T)+a3*cos(6π*t/T)+…+an*cos(2π*n*t/T)+…
- a0=2/T*∫(0<=t<=T/2,f(t)dt)
- an=4/T*∫(-T/2<=t<=T/2,f(t)cos(2π*n*t/T)dt)
関数f(x)が奇関数ならa0=0となり、以下の原点対称の波形となる。
- f(t)=b2*sin(2π*t/T)+b2*sin(4π*t/T)+b2*sin(6π*t/T)+…+bn*sin(2π*n*t/T)+…
- bn=4/T*∫(0<=t<=T/2,f(t)sin(2π*n*t/T)dt)
既に偶関数の波形を実数に、奇関数の波形を虚数に割り振る複素数関数を想起させる。
ところでフーリエ級数の考え方はそれぞれの有限期間で定義された関数f(t)が{1,cos(2π/T),sin(2π/T),cos(4π/T),sin(4π/T),…cos(2πn/T),sin(2πn/T),…}という「一時結合(定数倍の和)」された形で表現可能としている。そこで関数空間(ベクトル空間)の基底を調べてみると「1とcos(n*ω0*t)」「1とsin(n*ω0*t)」「cos(n*ω0*t)とsin(n*ω0*t)」「cos(n*ω0*t)とsin(n*ω0*t)(ただしm≠n)」「cos(n*ω0*t)とsin(n*ω0*t)(ただしm≠n)」の間にそれぞれ直交性が確かめられる。ここまで来るとマクローリン展開によって証明されたオイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θi)との親近性が益々強く感じられる様になる。
④-1.「フーリエ級数展開」にオイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θi)を用いると式が大幅に簡略化する。
有限期間-T/2<=t<=T/2で定義された関数f(x)は以下の「複素フーリエ級数(Complex Fourier series)」と「複素フーリエ係数(Complex Fourier coefficient)」で表される。
- f(t)=…+C-n*exp(-n*ω0*ti)…+C-3*exp(-3*ω0*ti)+C-2*exp(-2*ω0*ti)+C-1*exp(-ω0*ti)+C0+C1*exp(ω0*ti)+C2*exp(2*ω0*ti)+C3*exp(3*ω0*ti)…+Cn*exp(n*ω0*ti)…(複素フーリエ級数)
- Cn=1/T*∫(-T/2,T/2,f(t) exp(-n*ω0*ti)dt)(複素フーリエ係数)
- ω0=2π/T
和の記号Σを使えばf(t)の記述はさらに省略可能となる。
- f(t)=Σ(n=-∞,∞,Cn*exp(-n*ω0*ti))(複素フーリエ級数)
理工学分野では関数f(x)の複素フーリエ係数Cnをスペクトルと呼ぶ事がある。実際確かにそれは(各波形の成分一覧を並べた)スペクトルそのものといって良い。
①「三角波(Triangular wave)」や「放物線(Parabola)f(t)=t^2(-a<=t<=a)」の様な「(指数が偶数のCos関数の集合)偶関数系」の場合は、実数領域に波形がそのまま顕現する。
②「ノコギリ波(Sawtooth wave)」や「矩形波(Square wave)」の様な「(指数が奇数のSin関数の集合)偶関数系」の場合は、虚数領域に定数部を反映しない形で波形が顕現する。
定数項はあくまで表示エリア調整用?
④-2.ここから無限区間で定義され、かつ周期性を有さない関数f(x)を扱う「フーリエ変換(Fourier transform)」や「フーリエ逆変換(Fourier inverse transform)」 が派生する。
基本的戦略としては「有限区間におけるΣ(総和)」の「無限区間(-∞~∞)における∫(積分)」に置き換え、自然数nによる離散スペクトルを実数ωによる連続スペクトルに差し替えるというもの。
- フーリエ変換(Fourier transform)…複素フーリエ系数Cn=1/T*∫(-T/2,T/2,f(t) exp(-n*ω0*ti)dt)をF(ω)=∫(-∞,∞,f(t) exp(-i*ω*t)dt)に拡張。
- フーリエ逆変換(Fourier inverse transform)…複素フーリエ級数f(t)=Σ(n=-∞,∞,Cn*exp(-n*ω0*ti))をf(t)=1/2π*∫(-∞,∞,F(ω) exp(i*ω*t)dω)に拡張。
プリズム(prism)は異なる周波数の光が屈折率も異なる事を利用した分光器の1種であり、分けられた光の分布が連続スペクトルを構成する。
雨上がりの大気も同様の効果を示す事があり、かくして虹が現れる。
この様に「光のフーリエ解析」自体は以外と身近な存在。
整数でない実数は適当な有効数字の小数で表すのが実用的である.同じ
ことを関数でやるのがたとえばテイラー展開であり,フーリエ展開である。
*このドキュメントではMathematicaを活用しているが、このサイトだとRのRyacasライブラリの領分となる。
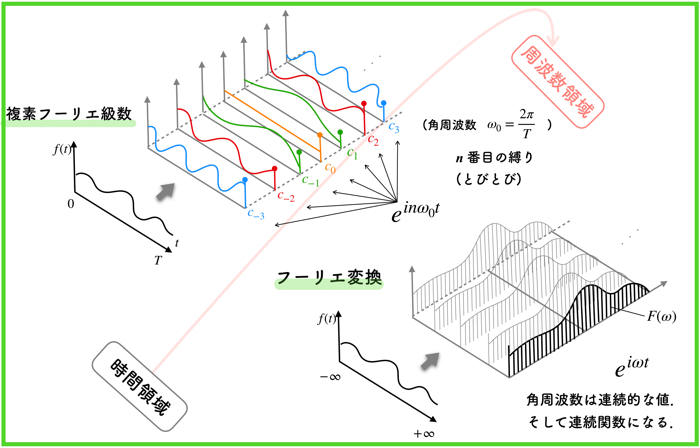
これと同じ成果に「関数空間(ベクトル空間)における各正弦波の直交基底」なる前提から出発して到達しようとすると(それぞれの角周波数の直交を証明する)「超関数」デルタ関数δ(x)に登場願わねばならない。
⑤-1.関数f(t)がフーリエ変換可能でF(ω)の値が定まる為には、その絶対値の積分∫(-∞,∞,|f(t)|dt)が有限確定地に収束せねばならない。その条件を満たさない関数群をまとめて救済したのが「ラプラス変換(Laplace transform)」となる。理論上の原点こそピエール=シモン・ラプラス(Pierre-Simon Laplace, 1749年〜1827年)の著作(1780年)にまで遡るが、回路方程式の解決に利用可能なほど実用レベルで磨き上げたのは英国の電気技師オリヴァー・ヘヴィサイド(Oliver Heaviside, 1850年〜1925年)の発表(1899年)を出発点とする。
そう、世の中には「パイレーツ・オブ・カリビアン(Pirates of the Caribbean、2003年〜)」に登場する「キャプテン・ジャックスパロウ(Capten Jack Sparrow)のコンパス」の如く単なるフーリエ変換だけではオイラーの単位円上の収束角度が導出出来ない関数が思うより沢山存在し、しかもそういう関数ほど利用頻度が高いから困り者だったりする。
ラプラス自身が考えたこれらの関数を絶対可積分(Absolute integrable)領域に引き戻さんとする対策は「対策の必要な元関数f(x)について、t→∞とすると非常に速く0に収束するy=exp(-Ct)(C>0)を掛け合わせf1(x)としてからフーリエ変換を遂行する」というもの。ではどの条件下でどの関数がかかる援用を受ける必要があるのか。それをまとめ上げたのが「叩き上げ」ヘヴィサイドという事になる。
- 基本形はf1(x)=f(t)*exp(-ct)={exp(-ct)(0<=t), 0(t<0)}。exp(-ct)は減衰関数なのでcを適当に選べばフーリエ変換時点の発散が食い止められる。積分表現としてはF(s)=∫(0,∞,f(t) exp(-st)dt)となる。sは複素数c+iωでcとωは実数。
*積分の下端が0なのを「片側ラプラス変換」というが、これが一般的なのは理工系の分野では時刻t=0スタートで現象を始動させ、その後の観察を続ける事が多いからだという。- 逆ラプラス変換は複素数の線積分そのもので経路積分ともいいf(t)=1/2πi∫(c-i∞,c+i∞,F(s) exp(s*t)ds)(t>=0)となる。
実際には以下の変換表を使う場合が多い。
- 普通に収束する場合は「t関数f(t)⇄s関数f(s)(f>=0)」
- N次関数は「t関数f(t)=1⇄s関数f(s)=1/S」「t関数f(t)=t⇄s関数f(s)=1/S^2」「t関数f(t)=t^N⇄s関数f(s)=N!/(S^(N+1))」
- ユニット関数の場合は「t関数f(t)=1⇄s関数f(s)=1/S」
- デルタ関数の場合は「t関数f(t)=δ(t)⇄s関数f(s)=1/S」
- 指数関数の場合は「t関数f(t)=exp(a*t)⇄s関数f(s)=1/(S-a)」
- 三角関数の場合は「t関数f(t)=cos(ω*t)⇄s関数f(s)=S/(S^2+ω^2)」「t関数f(t)=sin(ω*t)⇄s関数f(s)=ω/(S^2+ω^2)」
用途としては「回路方程式(Circuit equation)」や「線形応答理論(linear response theory)」など。ガチ工学系の世界…
ただノーバート・ウィーナー(Norbert Wiener, 1894年〜1964年)「サイバネティックス(Cybernetics 1961年)」にも通じるラプラスの悪魔(Laplace's demon)性、すなわち「全ての入力が制御下にあれば、全ての出力を制御下に置ける」万能感への陶酔も感じないではない。
そしてニューロン・ネットワーク分野の急先鋒だったパーセプトロン(Perceptron)研究はこの先入観故に一旦行き詰まり、「隠れ層」設定なるパラダイムシフトを経て新次元へと突入していく。
それにつけても本当にフーリエ解析(Fourier analysis)発展過程においてピエール=シモン・ラプラス(Pierre-Simon Laplace, 1749年〜1827年)とジョゼフ・フーリエ男爵(Jean Baptiste Joseph Fourier, Baron de、1768年〜1830年)それぞれが果たした役割の見極めが本当に難しいのですね…









