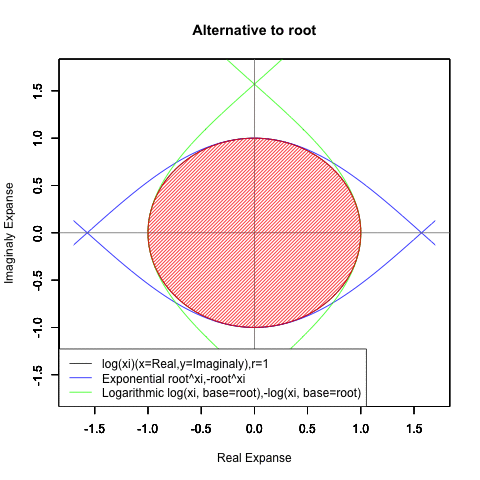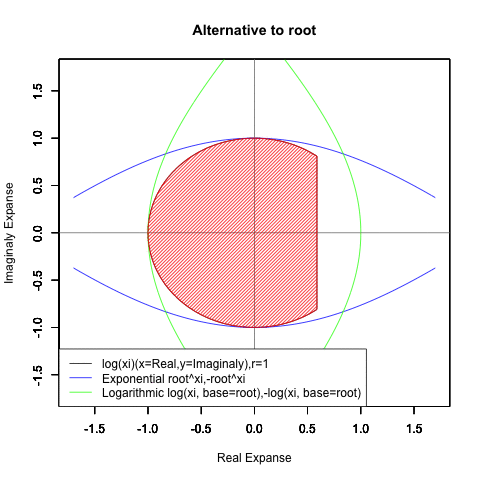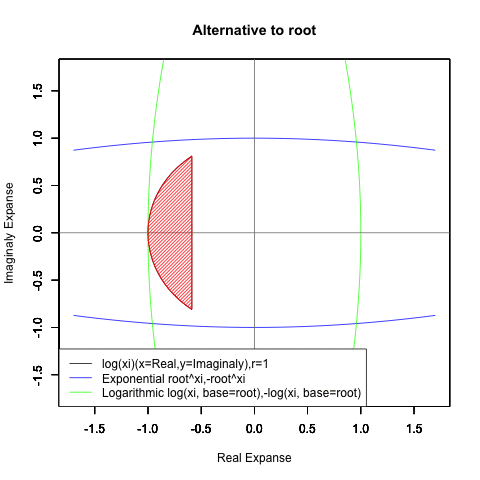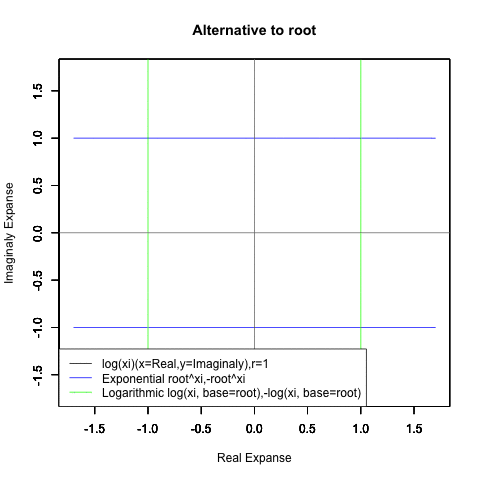
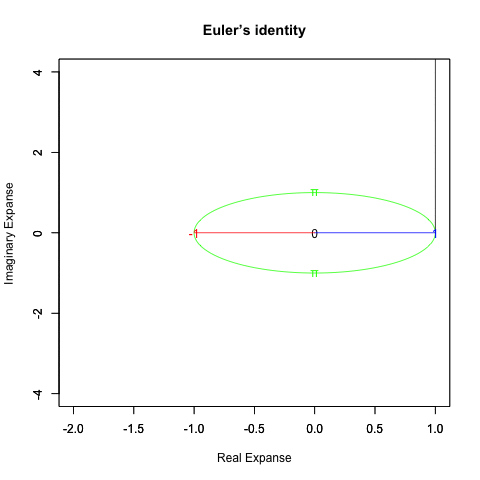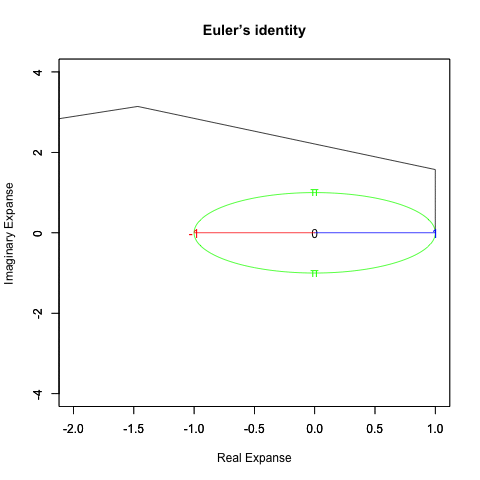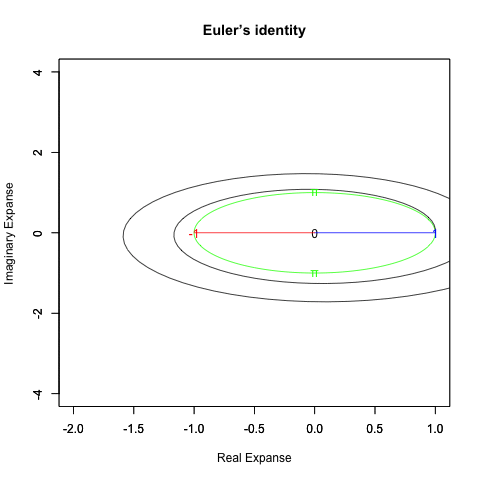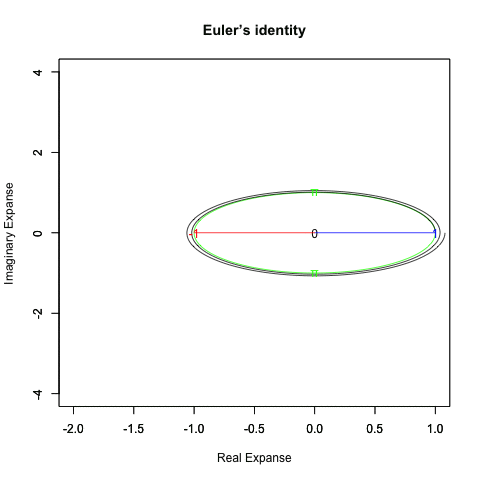
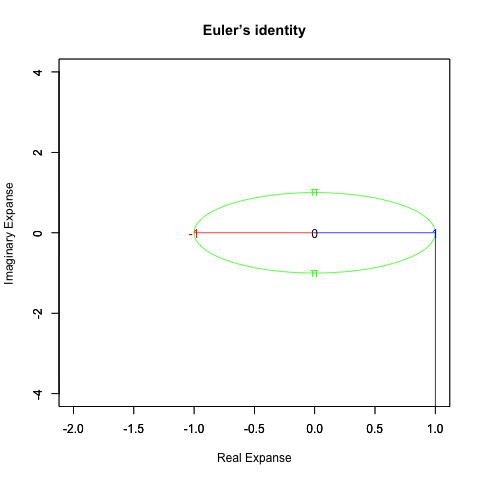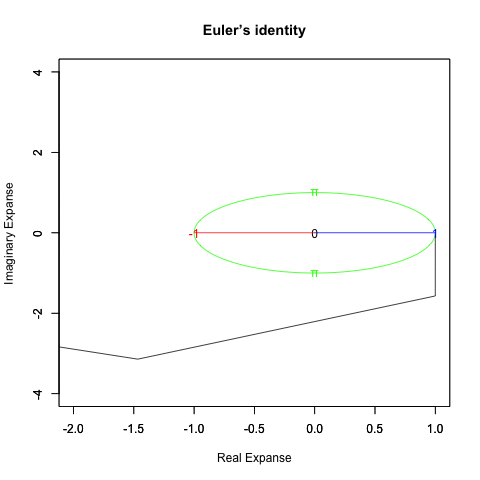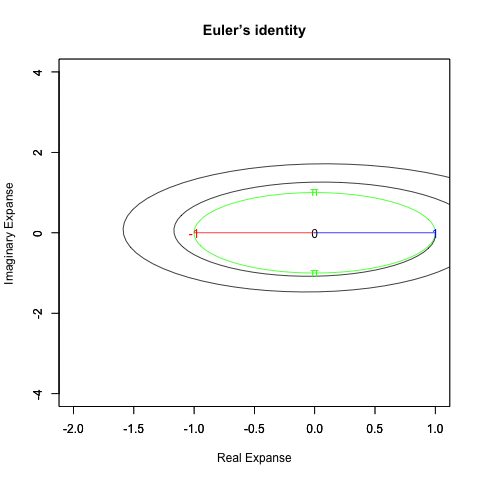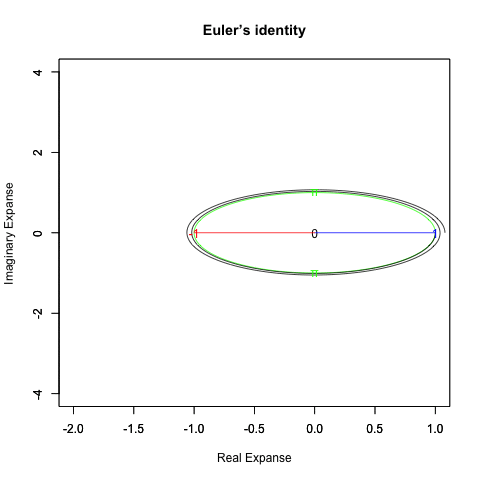
出発点はあくまで「オイラーの原始量(Euler's primitive sweep)=観測原点0を距離1ですっぽり包見込む全球型スクリーン」となります。
①任意の観測原点「0」を設置する。この時点ではまだ何も起こってはいない。
②何かが観測されると、たちまち観測原点「0」と対象「1」とを結ぶ距離1の半線分の旋回範囲に(これを半径とする)円周/円や球面/球が現出し「観測原点をすっぽり包む全球型スクリーン」として認識される。
「直径2」の概念が芽生える瞬間でもあり、その極限値は観測原点より半径分「1」あるいは半周分「π」離れた先に極限値「−1」。複素系座標でいうところの「1+πi=-1+0i」。
こうした考え方の大源流は「単位円(unit circle、原点0,半径1の円弧)の描き方」の確率過程に遡るのです。
半径が 1 の円のことである。
①解析幾何学(いわゆる“座標幾何”)では特に原点(すなわち x 軸と y 軸の交点) O(0, 0) を中心とするものをいう。これは、原点からの距離が 1 であるような点の全体が描く軌跡のことと言っても同じことである。
②しばしば S1 で表される(これは n 次元の球面 (sphere) という概念の n = 1 の場合という意味合いを含む)。
S1 = {x ∈ R^2 | dist(O, x) = 1} = {(x, y) ∈ R^2 | x^2 + y^2 = 1}.
- 太字の C あるいは黒板太字のℂ…複素数全体の成す集合
- R…実数全体の成す集合
単位円上の関数
単位円と三角関数との関係単位円上の任意の点の座標は、ある弧度 θ (0 ≤ θ < 2π) により正弦関数と余弦関数を用いて(cos θ, sin θ)と表される。これは三角関数の定義そのものである。
単位円上の関数は弧度を実数とみなすことにより、周期関数になる。周期関数のフーリエ展開は、単位円上の関数の既約指標による展開と見なされる。
ガウス平面上の単位円
複素数平面上の単位円は絶対値が 1 の複素数の描く軌跡{z ∈ C | |z| = 1} = {exp(iθ) | 0 ≤ θ < 2π}となる(exp は自然対数の底 e を底とする複素変数の指数関数)。これは、複素数の通常の積に関して閉じていて群を成し、円周群 (circle group) などと呼ばれることがある(これはまた 1 次元のユニタリー群と呼ばれるリー群であり、U(1) と記される。円周群は複素数平面において絶対値の定める通常の距離に関して、コンパクトな位相群である)。
任意の自然数nに対して円周群はただ一つの位数nの部分群をもつ。それは 1のn乗根の全体であり、1の原始n乗根で生成される巡回群である。
1の冪根(root of unity) - Wikipedia
数学において、冪乗して 1 になる(冪単である)ような数のことである。すなわち、ある自然数nが存在してz^n = 1となる z のことである。
通常は複素数の範囲で考えるが、場合によっては p 進数のような他の数の体系内で考える場合もある。以下では主として複素数の場合について述べる。自然数nに対しm (< n) 乗しても決して 1 にならず、n 乗して初めて 1 になるような 1 の冪根はn乗根として原始的 (primitive) であるという。自然数nを固定せず1の原始n冪根あるいは1の原始n乗根として得られる数を総称し「1の原始冪根(いちのげんしべきこん)または「1の原始累乗根(いちのげんしるいじょうこん)」という。
1の原始冪根
複素数の範囲では、1 の原始 n 乗根は n ≥ 3 のとき2つ以上存在する。ド・モアブルの定理より、1の原始n乗根の一つはζ^(1/n)=Cos(2π/n)+Sin(2π/n)iで与えられることが分かる。この時、ζ^(1/n)の共役複素数ζ^(1/n)も1の原始n乗根である。nと互いに素な(a, b の最大公約数 gcd(a, b) が1)自然数mに対してξ^(1/n)^mは1の原始 n 乗根であり、逆に 1 の原始n乗根はこの形に表せる。すなわち、1の原始n乗根は、オイラーのφ関数を用いて、ちょうどφ(n)個存在する。
方程式x^n = 1を考える。この方程式の根は、ド・モアブルの定理よりx=Cos(k*2π/n)+Sin(k*2π/n)i(ただし0≤k≤n-1)であるが、1の原始n乗根ξ^(1/n)を一つ選べばξ^(1/n)^k(ただし0≤k≤n-1)と書くことができる。
また上記のように根を三角関数で表すことは容易であるが、それが根号を用いて表示できること、つまり方程式が代数的にも可解であることはガウスにより証明された。
具体例
以下、iは虚数単位である。
- ζ(ゼータ)^2=-1
- ζ^3=(-1±sqrt(3)i)/2 *しばしば「ω(オメガ)」と書かれる
- ζ^4=±i
- ζ^5=(-1+sqrt(5)±sqrt(10+2sqrt(5)))i/4,(-1-sqrt(5)±sqrt(10+2sqrt(5)))i/4
- ζ^6=(1±sqrt(3)i)/2
- ζ^8=(sqrt(2)±sqrt(2)i)/2,(-sqrt(2)±sqrt(2)i)/2
1 の冪根は全て、ガウス平面における単位円上にある。また概要で述べたことは1のn乗根の全体が位数nの巡回群となることを示している。
【古典幾何学】単位円の方程式x^2+y^2=1
ピタゴラスの定理z=sqrt(x^2+y^2)の応用だが、半円しか描けない。これ実は「愛の正反対は無関心(相関係数0)か、それとも憎悪(相関係数マイナス)か?」なる設問を経て直交概念、すなわち線型従属(一次従属)でない線型独立 (linearly independent、一次独立ともいう) に至る重要な数理モデル設定上の課題だったりする。
解析幾何学において「(a, b) を中心とする半径 r の円」は(x-a)^2+(y-b)^2=r^2を満たす点 (x, y) 全体の軌跡である。この方程式を、円の方程式と言う。これは、中心 (a, b) と円上の任意の点 (x, y) との二点間の距離が r であるということを述べたものに他ならず、半径を斜辺とする直角三角形にピタゴラスの定理を適用しすることで導出できる(直角を挟む二辺は、各座標の絶対差 |x − a|, |y − b| を長さとする)。
中心を原点に取れば、方程式は「x^2+y^2=r^2」と簡単になる。この形(x2, y2 の係数が等しく、xy の項を持たない)の方程式が与えられたとき、以下の何れか一つのみが成り立つ:
- ρ < 0 のときは、この方程式に解となる実点は存在しない。この場合を虚円(imaginary circle) の方程式と呼ぶ。
- ρ = 0 のとき、方程式 f(x, y) = 0 は中心となる一点 O := (a, b) のみを解とし、点円(point circle) の方程式と言う。
- ρ > 0 のときには、f(x, y) = 0 は O を中心とする半径 r := √ρ の円、あるいは実円 (real circle)の方程式になる。
α = 0 のとき f(x, y) = 0 は直線の方程式であり、a, b, ρ は(射影平面上で、あるいは見かけ上)無限大になる。実は、直線を「無限遠点を中心とする半径無限大の円」と考えることができる。
統計言語Rによる実証例
#「x^2+y^2=1」だけでは半円しか描けない
f0<-function(x){sqrt(1-x^2)}
plot(f0, xlim=c(-1,1),ylim=c(0,1),type="l",main="The Circle ploting x^2+y^2=1", xlab="x", ylab="y")

実際的な対応策は実にシンプル。プラス領域で半円を描く関数y=sqrt(1-x^2)のグラフとマイナス領域で半円を描く関数y=-sqrt(1-x^2)のグラフを同時表示すれば良いのです。
統計言語Rによる実証例
#y=-sqrt(1-x^2)のグラフ
f0<-function(x){-sqrt(1-x^2)}
plot(f0, xlim=c(-1,1),ylim=c(-1,0),type="l",main="The Circle ploting x^2+y^2=1(reverse)", xlab="x", ylab="y")

#y=sqrt(1-x^2)のグラフとy=-sqrt(1-x^2)のグラフの同時表示
f0<-function(x){sqrt(1-x^2)}
plot(f0, xlim=c(-1,1),ylim=c(-1,1),type="l",main="The Circle ploting x^2+y^2=1", xlab="x", ylab="y")
par(new=T)#上書き指定
f1<-function(x){-sqrt(1-x^2)}
plot(f1, xlim=c(-1,1),ylim=c(-1,1),type="l",main="", xlab="", ylab="")

【古典物理学】X軸にCos(θ)、Y軸にSin(θ)を配置
ある種の循環論法だが、ネイピア数e(1/e)も複素数も登場しないので使い勝手はそれなりに良い。とはいえ何か「蕎麦屋のカレー」みたいなアウェー感が漂う。
①等速円運動(Uniform circular motion)をX軸側とY軸側からそれぞれ観測。
②結果としてX軸観測結果としてCos(θ)関数、Y軸観測結果として(Cos波と同波形ながら位相が90度ズレている)SIN(θ)関数の写像を獲得し「直交し互い違いに単振動する2つの調和振動子(Harmonic oscillator)」なる物理モデルを組み上げる。
③かかる2つの調和振動子(Harmonic oscillator)をそれぞれX軸とY軸に配置して観察環境を再現すると単位円(原点0,半径1の円弧)もまた再現される。
統計言語Rによる実演例「最もシンプルな円の描き方」
theta <- seq(pi, -pi, length=360)
plot(cos(theta), sin(theta),xlim=c(-2,2),ylim=c(-2,2), type="l",col=rgb(0,1,0), main="Simple Circle Draw", xlab="cos(x)", ylab="sin(x)")

統計言語Rによる3D表示(z軸=t)
library(rgl)
complex_plane_z<-seq(-3*pi,3*pi,length=180)
complex_plane_x<-cos(complex_plane_z)
complex_plane_y<-sin(complex_plane_z)
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")


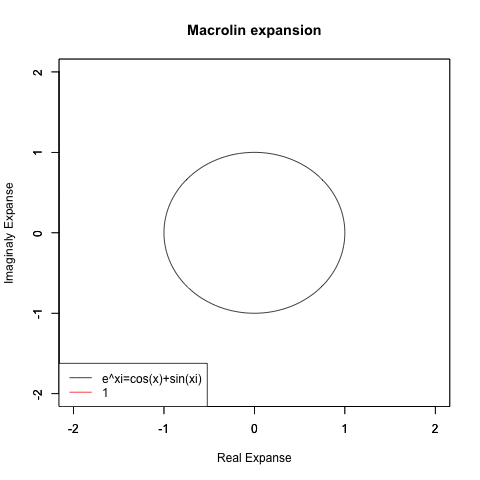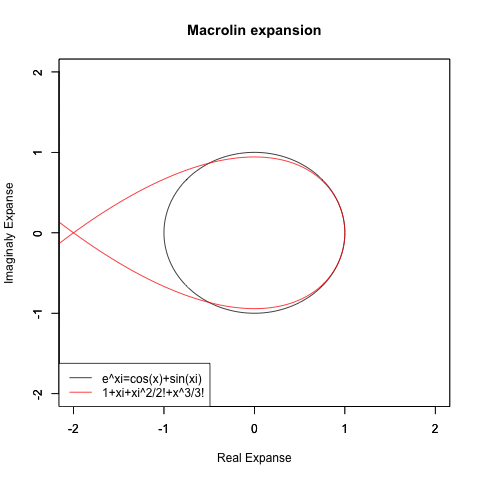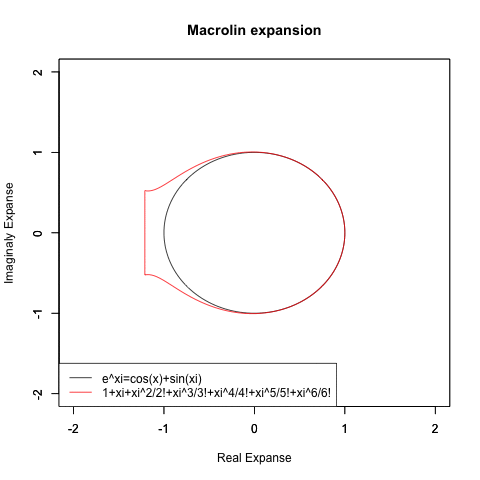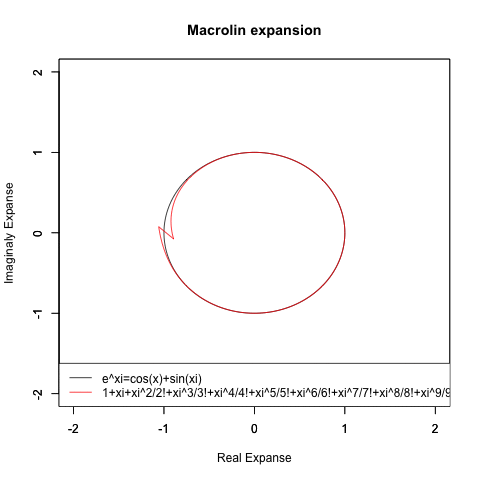
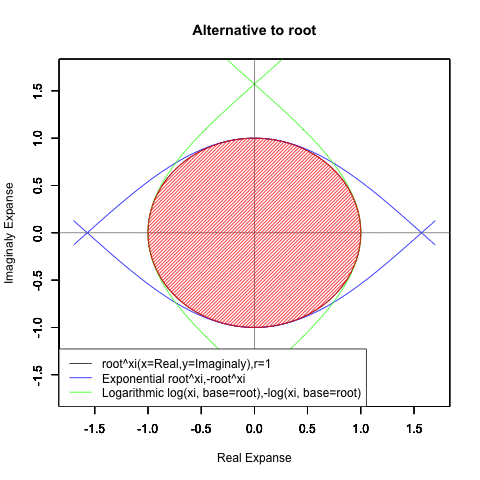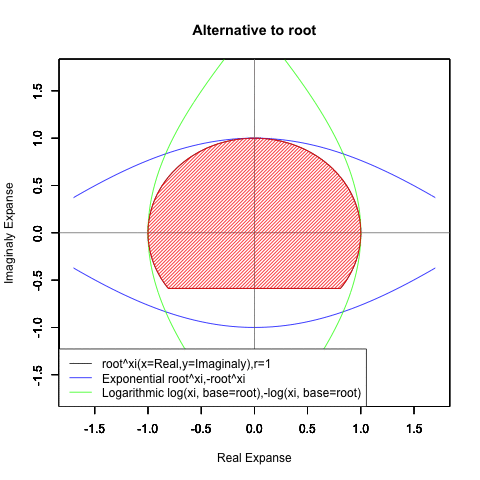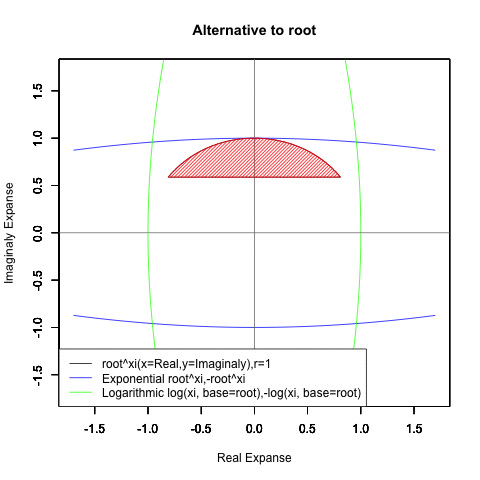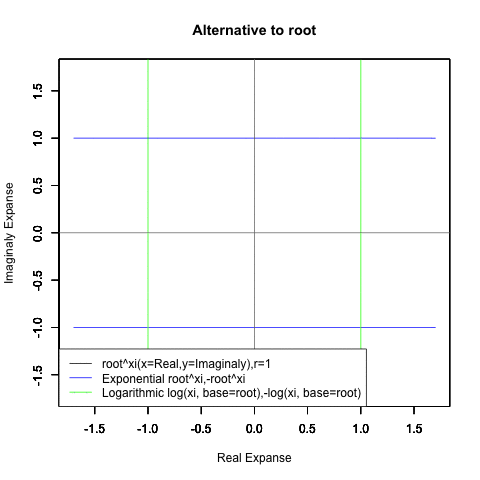
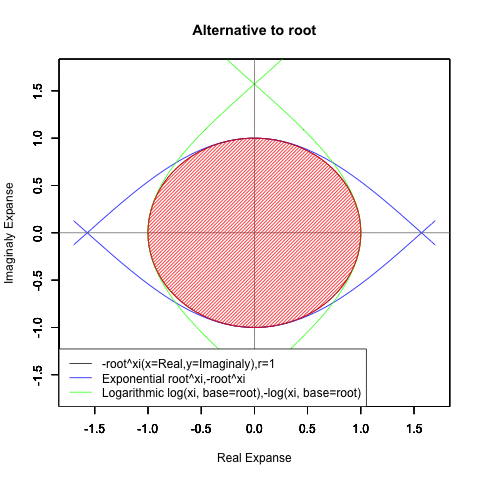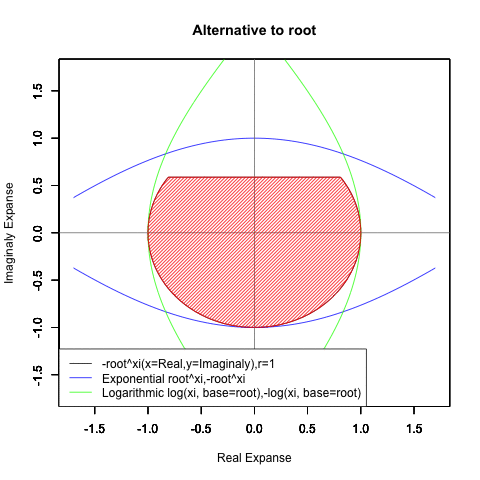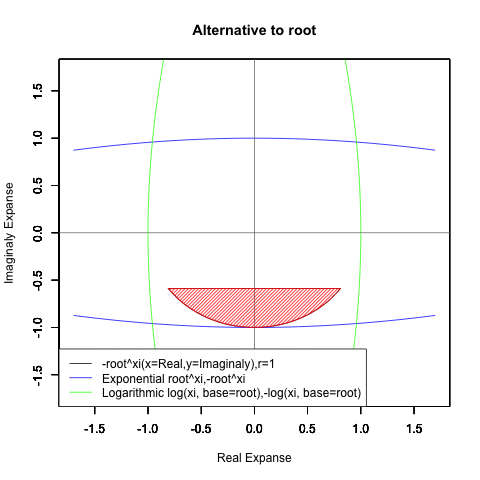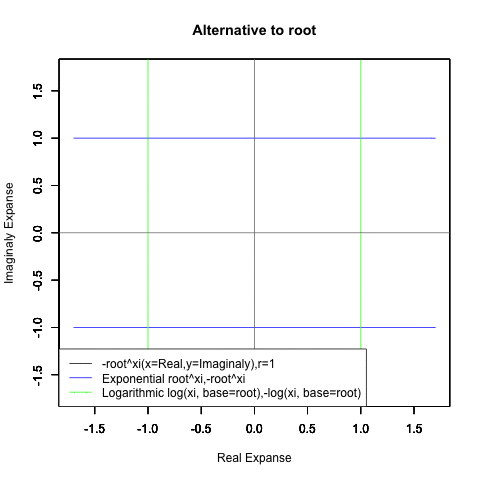
【指数・対数関数と三角関数と複素数平面の統合】オイラーの公式e^θi=(1±θi/N)^N=Cos(θ)+Sin(θi)に至るまでの一連の流れ。
まずは指数関数a^xあるいは対数関数Log(x,base=a)とは何かについて。
自然指数関数e^xと自然対数関数log(x)の特異性について。
そして複素数Xiが関数に与える影響について。
全体像を俯瞰すると…
どうして複素数Xi(0+1i)を指数関数a^xや対数関数Log(x,base=a)に与えると円が描かれるのでしょうか?
①要するに円弧はプロッティング上、絶対値を同じくする周期関数2つを90度位相をズラしてx軸とy軸に割り振ると描かれる。
②ところで指数関数a^xは無限に続く奇関数と偶関数の連続である。
③そして複素数Xi(x*(0+1i))を与えられた関数は偶関数を実数部、奇関数を複素数部に割り振る(絶対値=原点からの距離は変わらない)。
④だから実数部をX軸、複素数部をY軸に割り振ると、例えば(偶関数の集合たる)Sin関数と(奇関数の集合たる)Cos関数が綺麗に分離される(Cos(θ)+Sin(θi))。
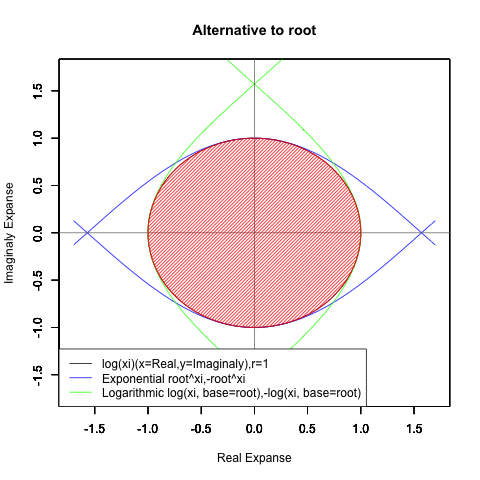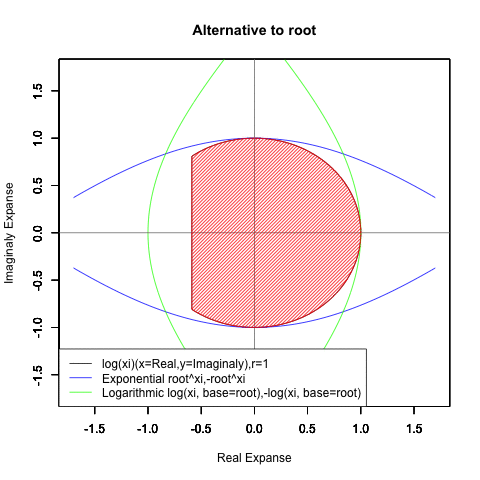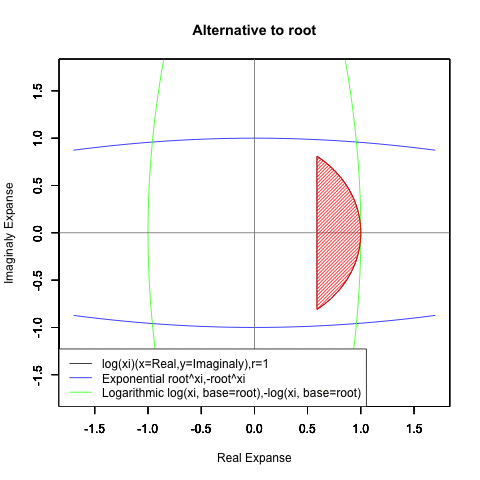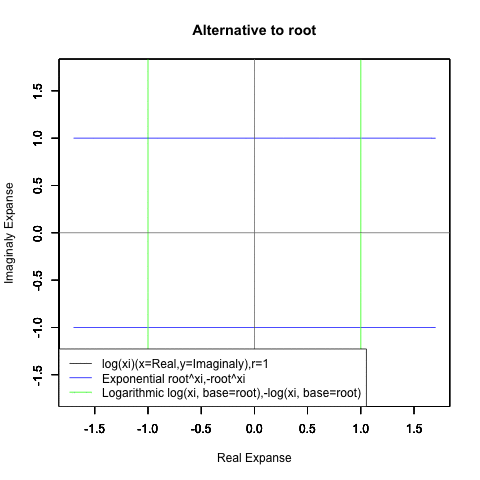
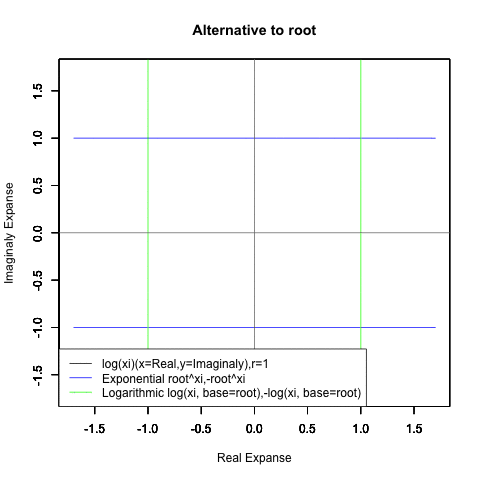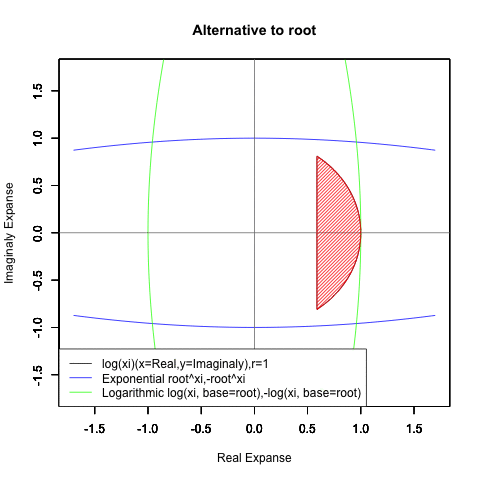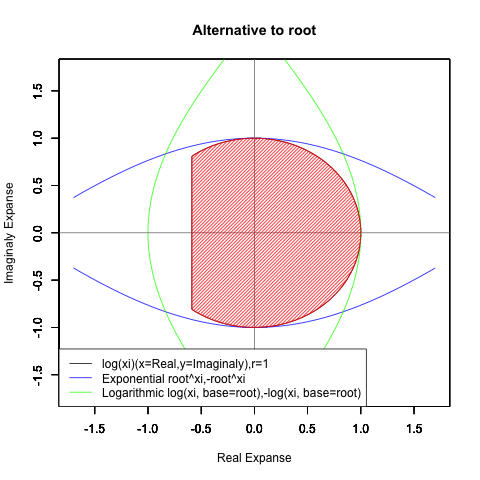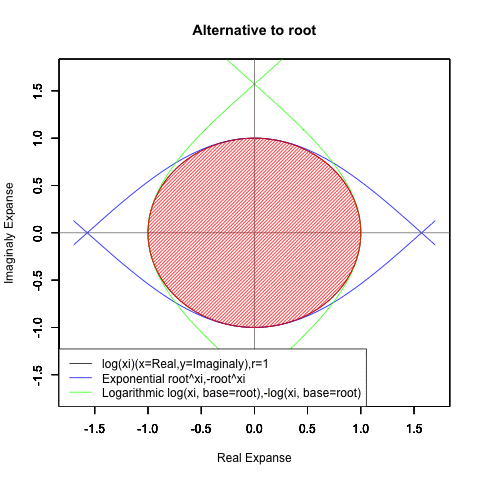
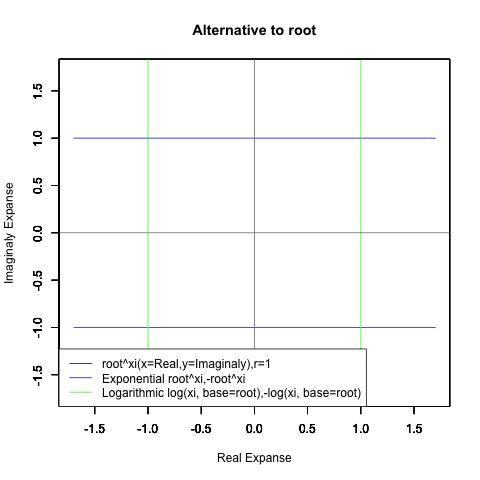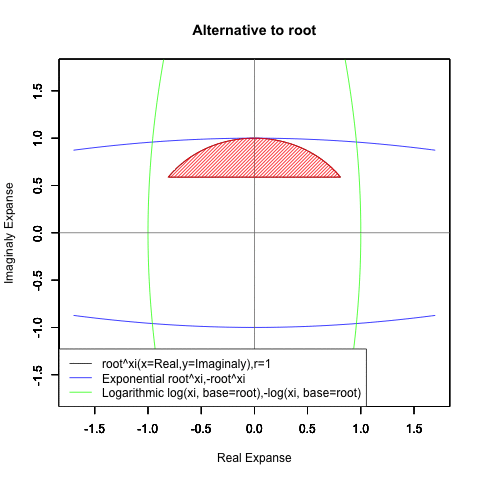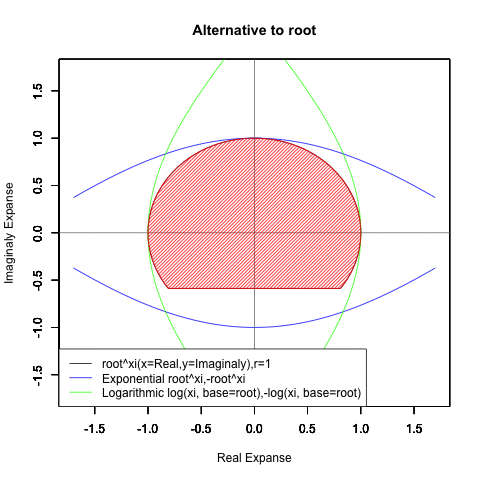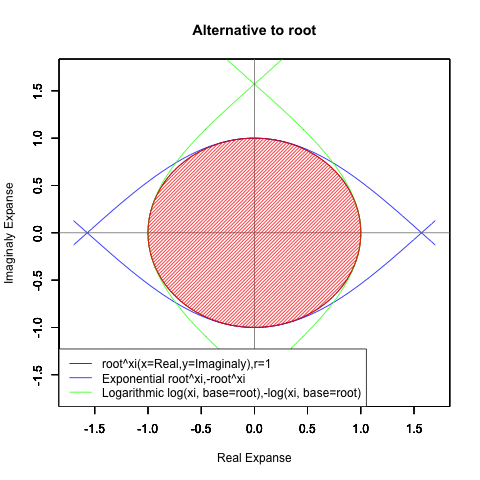
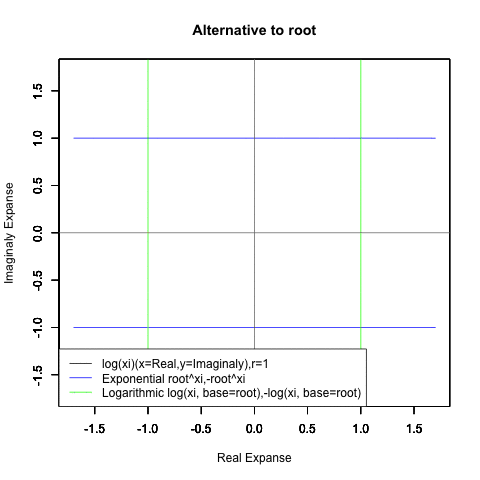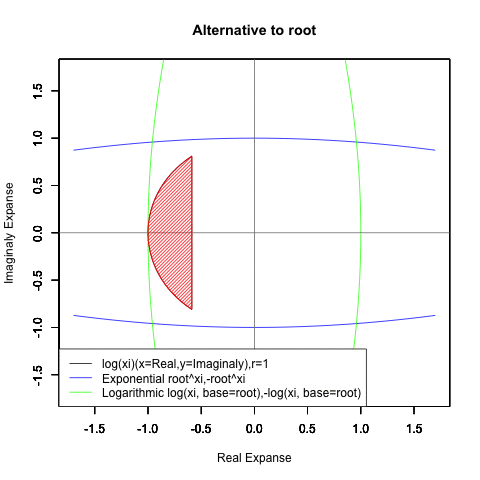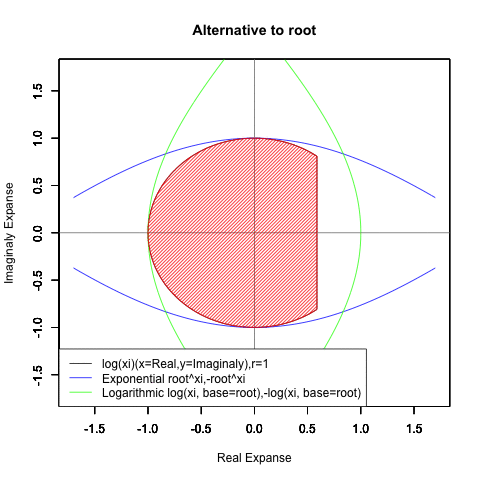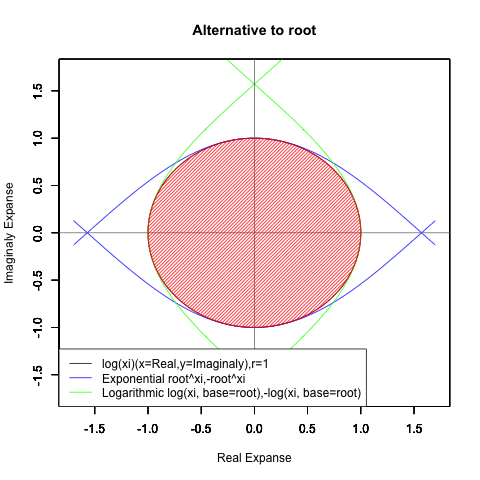
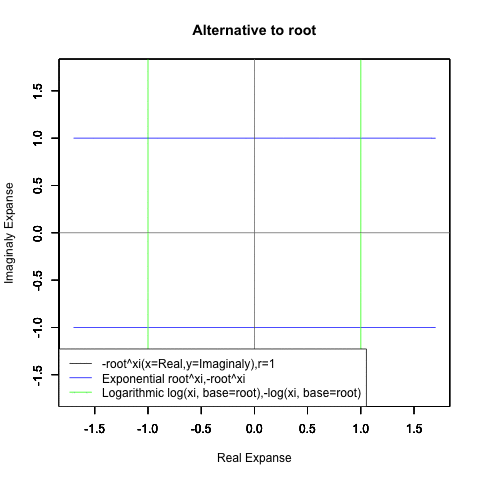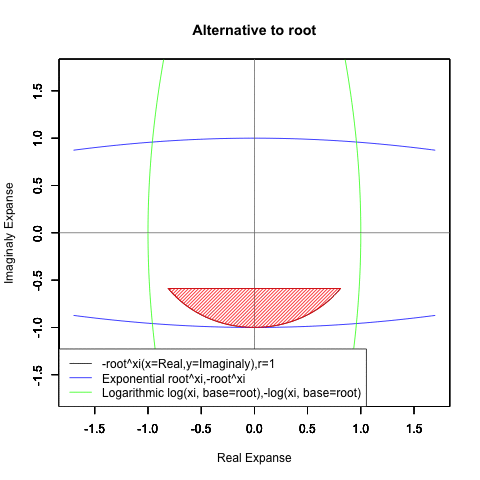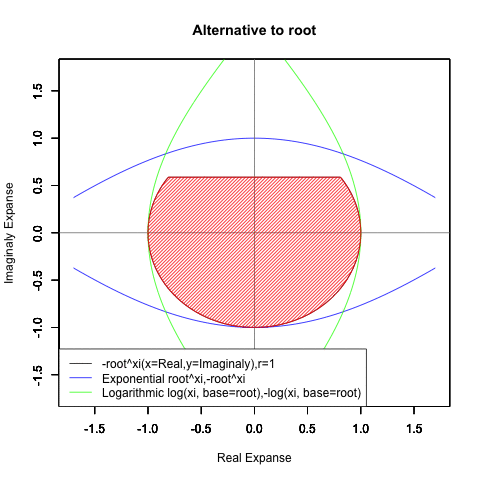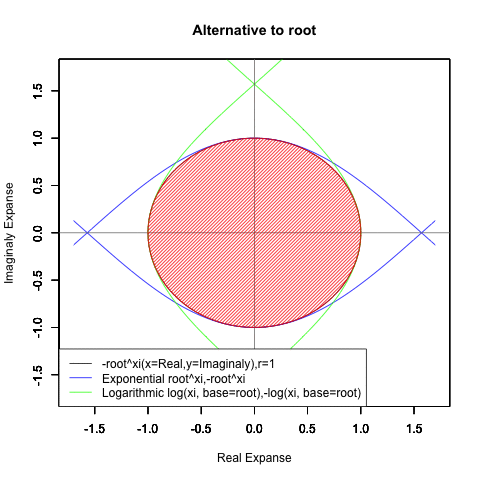
⑤ただし指数関数Y=a^Xiや対数関数Y=Log(Xi,base=a)が「ちゃんと1回だけ」円を描くのは底(root)をネイピア数e(exp(1)=2.718282)もしくは1/e(exp(-1)=0.3678794)とする以下の8種類の自然指数関数と自然対数関数だけだったりする。
Y=Log(Xi,base=exp(-1))
Y=Log(Xi)
Y=(1/e)^Xi
Y=e^Xi
Y=-Log(Xi,base=exp(-1))
Y=-Log(Xi)
Y=-(1/e)^Xi
Y=-e^Xi
⑥円弧の周期単位としてのπ(3.141593)に新たな意味が付与されるのもこれ以降。かくして人類はピタゴラスの定理がもたらした「半円しか描けない呪い」からの脱却に成功したのだった。
たかが単位円、されと単位円?