幾何学上の1角形(頂点や辺や面の概念が全て1点上に集約する図形。球表面上においてのみ認識可能)は、その時点で既に「回転の向き」なる価値観を有しています。

- 言い方を変えればこの時点で既に等速円運動が可能であり「右回り(時計回り)」「左回り(反時計周り)」の2種類の状態を備え得る。その影響は既にこれをX軸とY軸それぞれの観察結果から単振動を得た段階から始まっている。

- 実際、右手座標系においては円描画に際して「X軸に(初期値がX=1,Y=0の)コサイン波Cos(θ)」「Y軸に(初期値がX=0,Y=1)サイン波Sin(θ)」が与えられる。

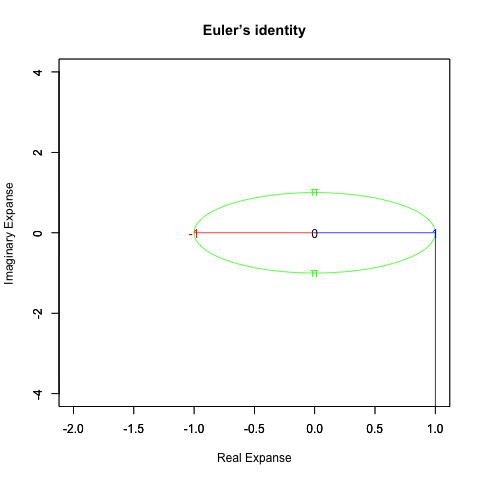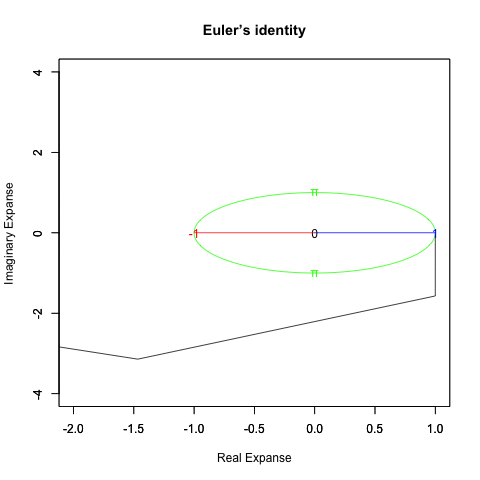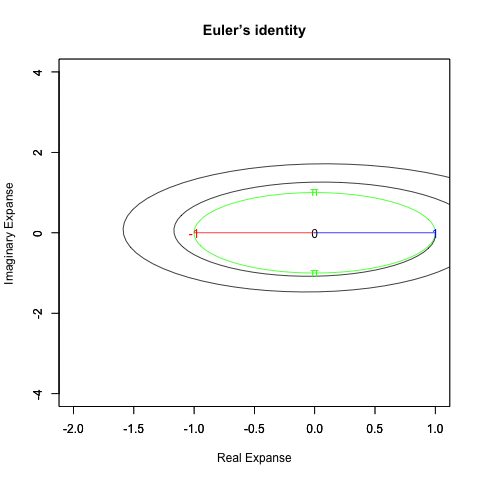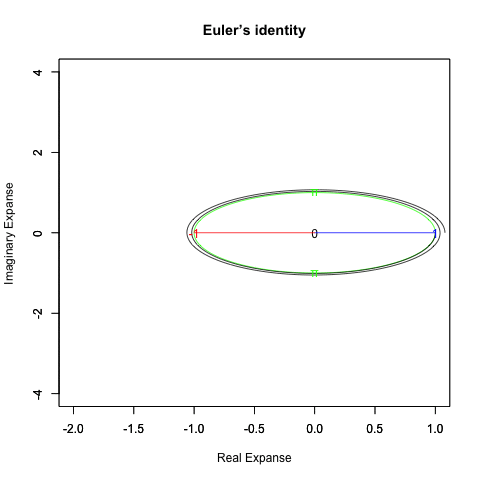
まさしくオイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θi)の世界だが、最初にその結論に到達したのは果たして数学界だったのか、それとも物理界だったのか…
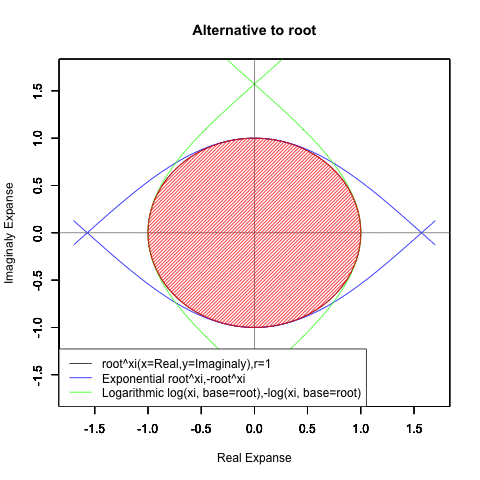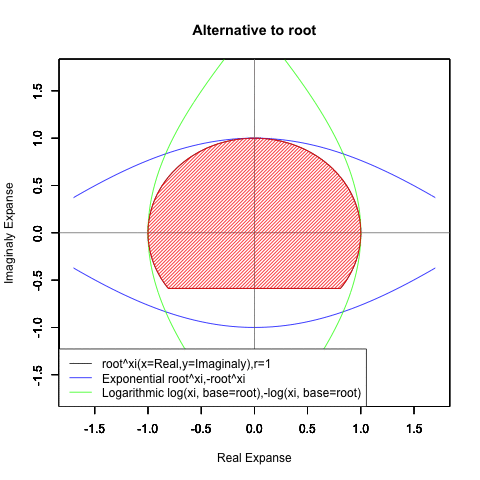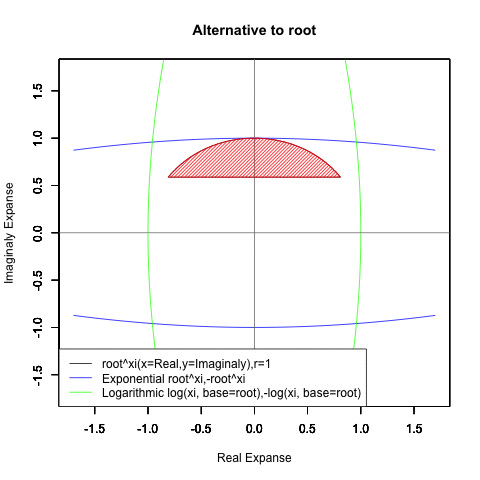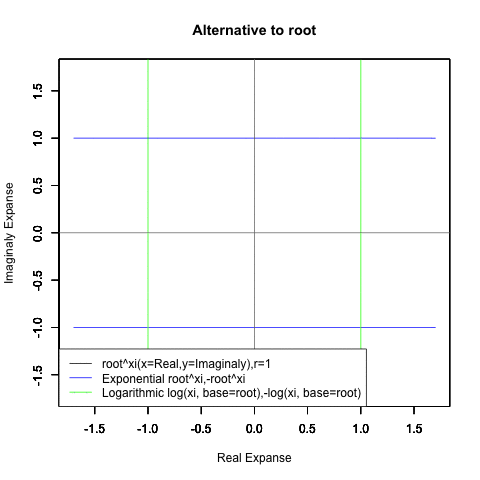
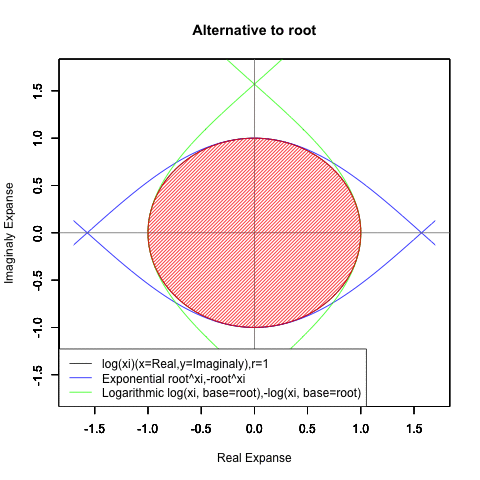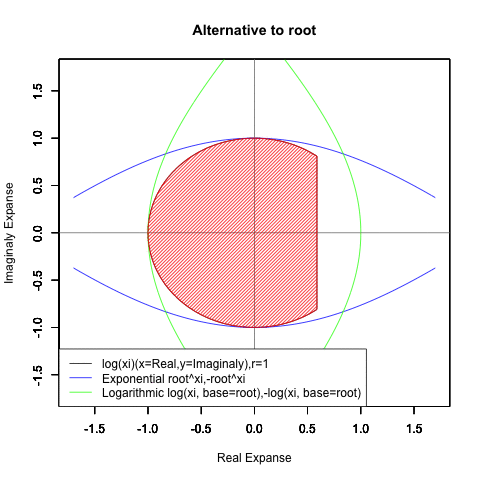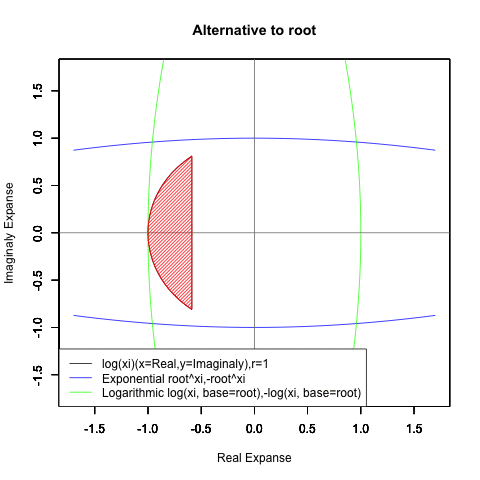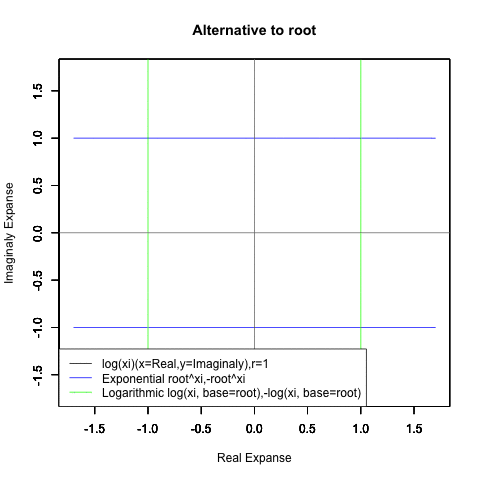
①いずれにせよ数学の世界における最初の完全円描画は(連続して偶関数と奇関数が出現し続ける)指数a^x・対数関数log(x,base=a)と(「i^2=-1」なる単純な判断基準で偶関数を実数、奇関数を奇数に割り振る)複素数の組み合わせによって達成され、その過程を通じて(円を描く周期としての)ネイピア数eとその逆数たる1/eを底(root)とする自然指数関数±e^θi/(1/e)^θiと自然対数関数±log(θi)/log(θi,base1/e)、および(指数に対応する円弧の変動単位としての)πの特別性が確認される運びとなった。
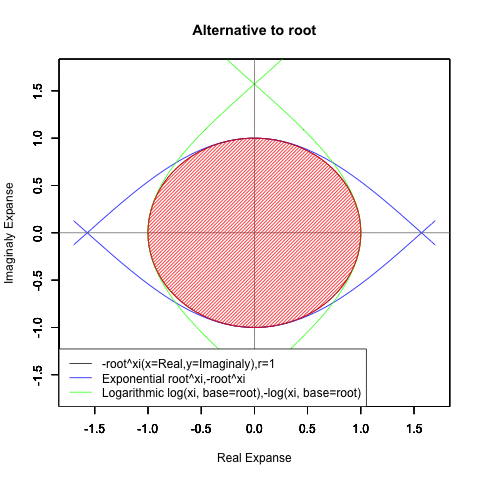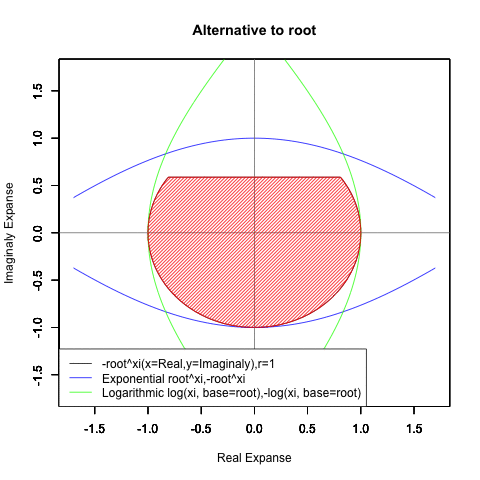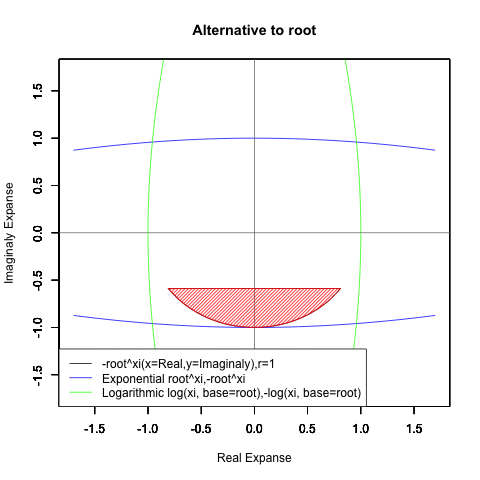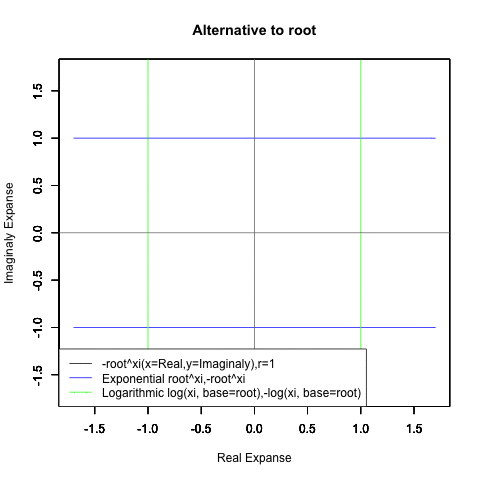
- XY座標(1,0)が原点…自然対数関数Y=log(θi)/log(θi,base=1/e)の場合
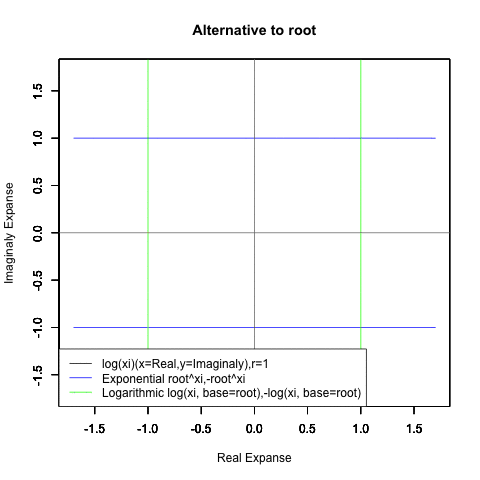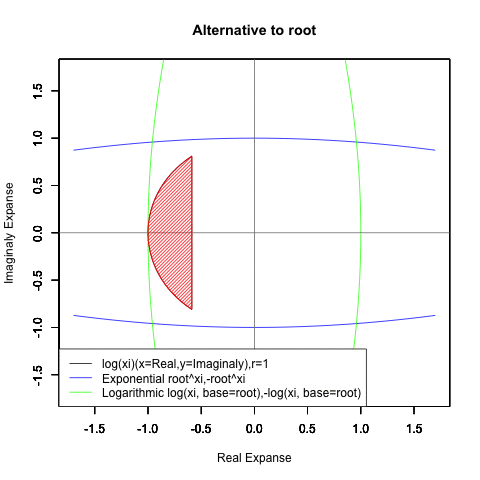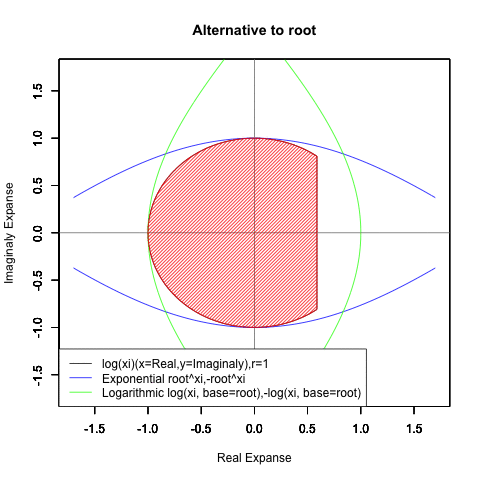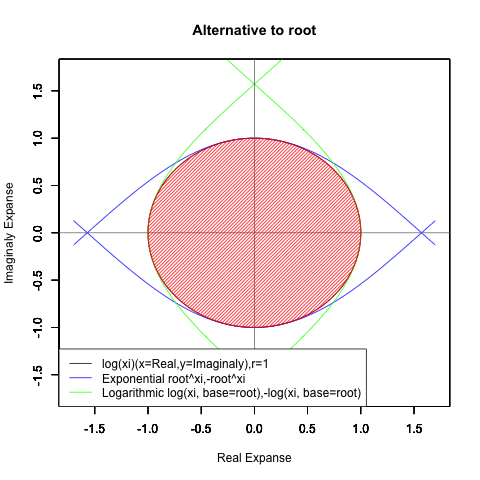
Log(Xi,base=exp(-1))からexp(0)=1へ底(root)を遷移させる→円が左から右に消失。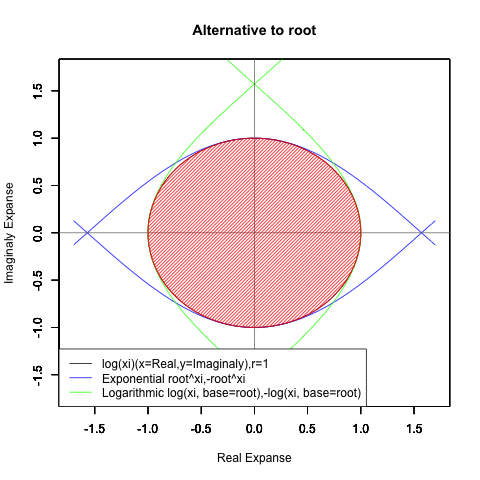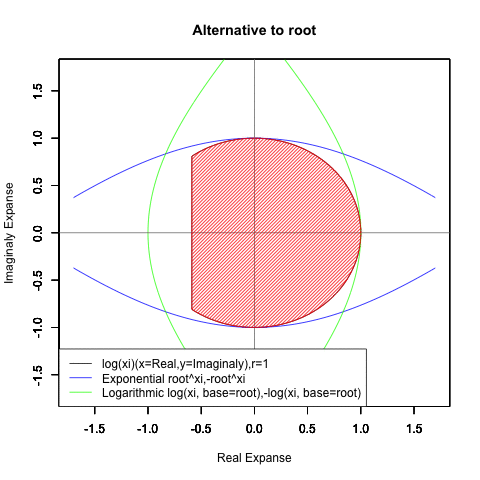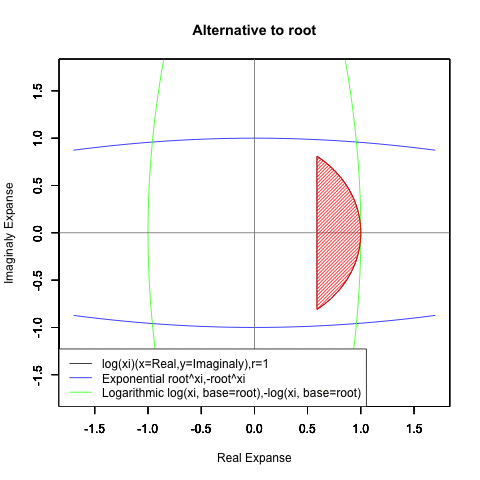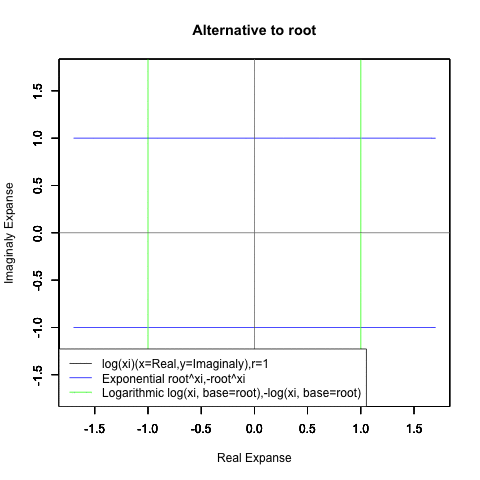
exp(0)=1からLog(Xi)へ底(root)を遷移させる→円が右から左に出現。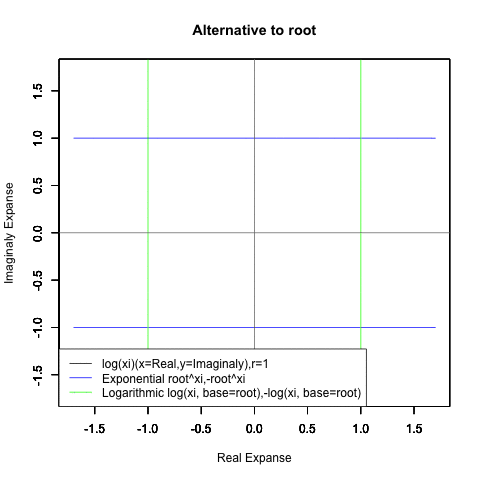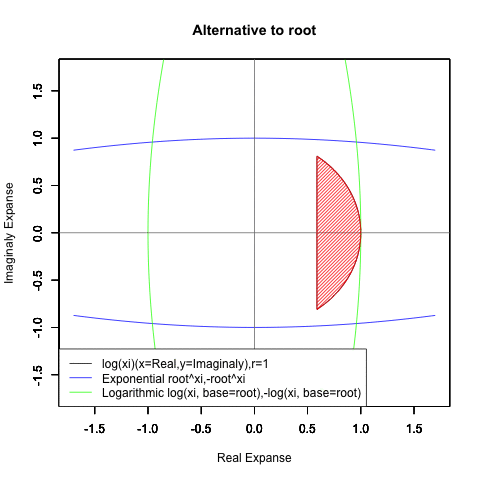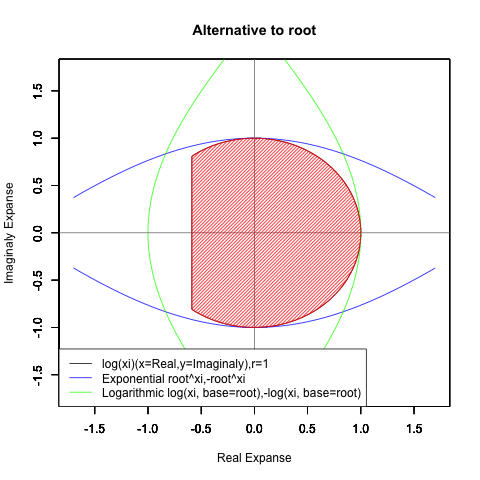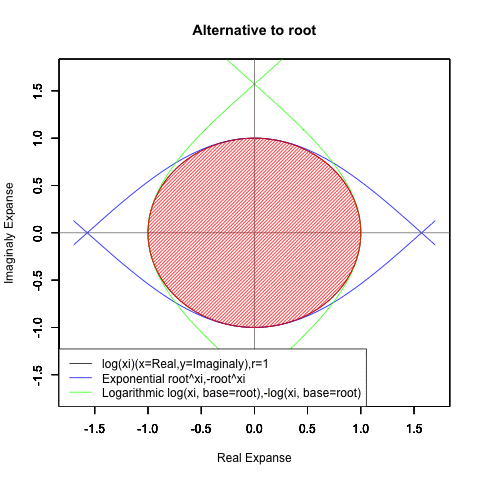
- XY座標(0,1)が原点…自然指数関数Y=e^θi/(1/e)^θiの場合
(1/e)^Xiからexp(0)=1へ底(root)を遷移させる→円が下から上に消失。
exp(0)=1からe^Xiへ底(root)を遷移させる→円が上から下に出現。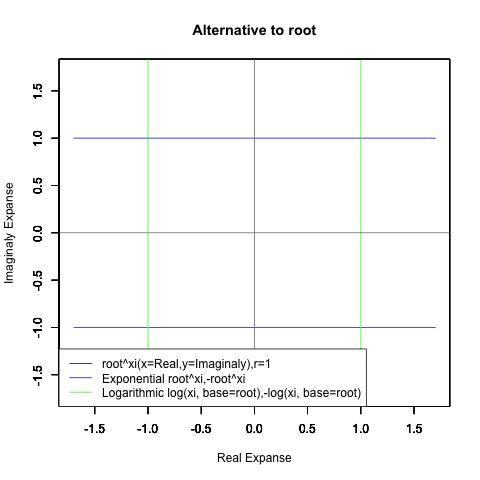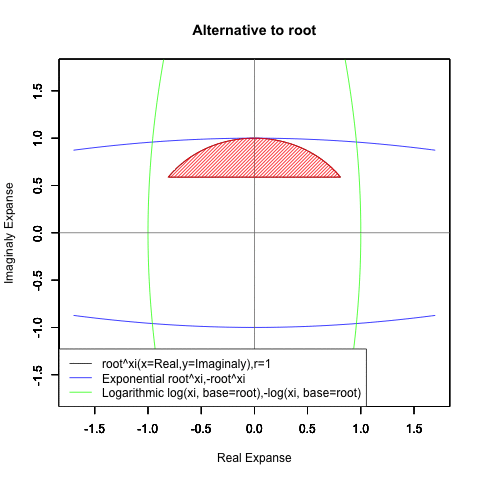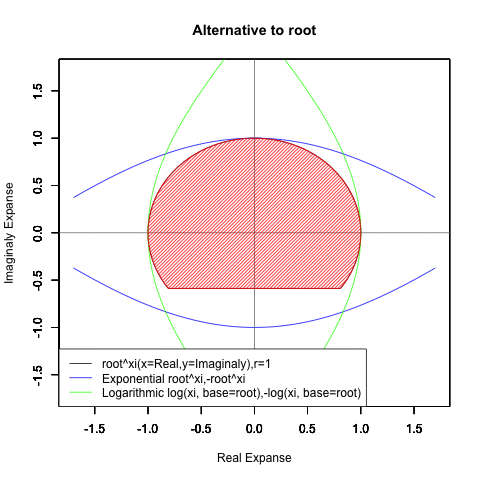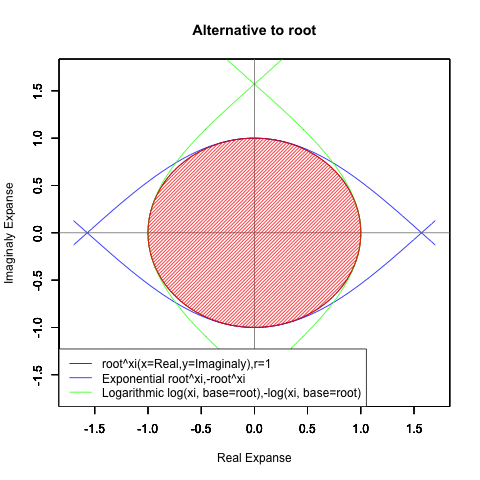
- XY座標(-1,0)が原点…自然対数関数Y=-log(θi)/-log(θi,base=1/e)の場合
-Log(Xi,base=exp(-1))からexp(0)=1へ底(root)を遷移させる→円が右から左に消失。
exp(0)=1から-Log(Xi)へ底(root)を遷移させる→円が左から右に出現。
- XY座標(0,-1)が原点…自然指数関数Y=-e^θi/(1/e)^θiの場合
-(1/e)^Xiからexp(0)=1へ底(root)を遷移させる→円が上から下に消失。
exp(0)=1から-e^Xiへ底(root)を遷移させる→円が下から上に出現。
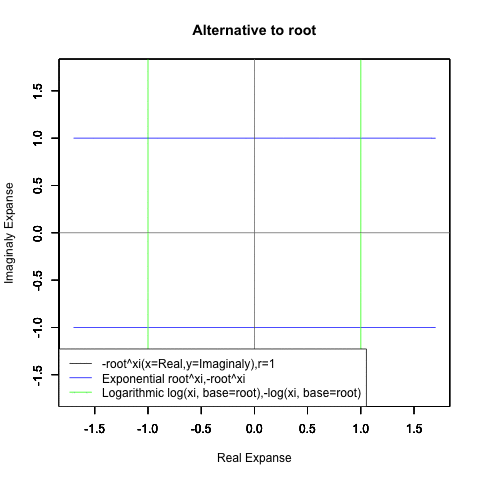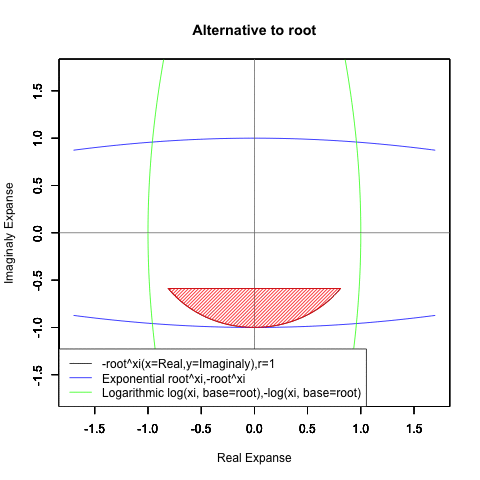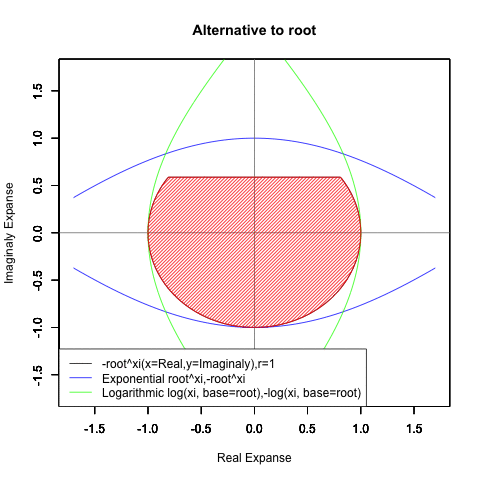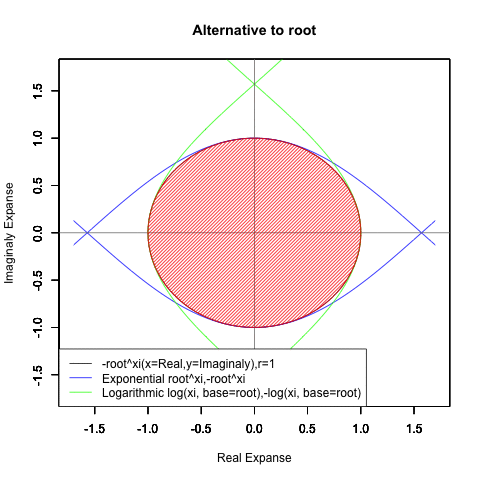
ちなみに底(root)が<1/eあるいは>eの時、円は折り返し多重に描かれる。
根(root)が1/e以下

根(root)がe以上

各関数の座標(Coordinates)遷移
function_names<-c("log(θi)","log(θi,base=1/e)","e^θi","(1/e)^θi","-log(θi)","-log(θi,base=1/e)","-e^θi","-(1/e)^θi")
radian_zero<-c("(00,+1)","(00,+1)","(+1,00)","(+1,00)","(00,-1)","(00,-1)","(-1,00)","(-1,00)")
radian_pi_harf<-c("(+1,00)","(-1,00)","(00,+1)","(00,-1)","(-1,00)","(+1,00)","(00,-1)","(00,+1)")
radian_pi<-c("(-1,-1)","(-1,-1)","(-1,-1)","(-1,-1)","(+1,+1)","(+1,+1)","(+1,+1)","(+1,+1)")
radian_pi_one_and_harf<-c("(-1,00)","(+1,00)","(00,+1)","(00,+1)","(-1,00)","(+1,00)","(00,+1)","(00,-1)")
Unit_Circle<-data.frame("Function_Names"=function_names,"Zero_θ"=radian_zero,"Harf_πθ"=radian_pi_harf,"πθ"=radian_pi,"One_and_harf_πθ"=radian_pi_one_and_harf)
library(xtable)
print(xtable(Unit_Circle),type="html")
| Function_Names | Zero_θ | Harf_πθ | πθ | One_and_harf_πθ | |
|---|---|---|---|---|---|
| 1 | log(θi) | (00,+1) | (+1,00) | (-1,-1) | (-1,00) |
| 2 | log(θi,base=1/e) | (00,+1) | (-1,00) | (-1,-1) | (+1,00) |
| 3 | e^θi | (+1,00) | (00,+1) | (-1,-1) | (00,+1) |
| 4 | (1/e)^θi | (+1,00) | (00,-1) | (-1,-1) | (00,+1) |
| 5 | -log(θi) | (00,-1) | (-1,00) | (+1,+1) | (-1,00) |
| 6 | -log(θi,base=1/e) | (00,-1) | (+1,00) | (+1,+1) | (+1,00) |
| 7 | -e^θi | (-1,00) | (00,-1) | (+1,+1) | (00,+1) |
| 8 | -(1/e)^θi | (-1,00) | (00,+1) | (+1,+1) | (00,-1) |
②ここで左回り(反時計回り)=プラス方向、右回り(時計回り)=マイナス方向が確定するのは自然指数関数e^θiの定義が(ネイピア数eを極限値とする)複利計算式e^1=(1+1/N)^Nに由来する(1+θi/N)^Nであり、e^-θiの定義が(ネイピア数eの逆数たる1/eを極限値とする)ベルヌーイ試行e^-1=(1-1/N)に由来する(1-θi/N)^Nであるからである。
以下はヤコブ・ベルヌーイ(Jakob Bernoulli、1654年〜1705年)自身の手になる大数の弱法則 (WLLN: Weak Law of Large Numbers)すなわち「独立同分布に従う可積分な確率変数の無限列 X1, X2, …が与えられてその平均をμと置く時、標本平均のとる値がそれから外れる確率は、十分大きな n を取ればいくらでも小さくできる」法則の証明ともなっている。
- ベルヌーイは1683年に複利計算式複利計算式(1+1/N)^Nから指数関数を導出した。まず「原資1を預けると1年で利息1がついて倍以上になる」夢の金融商品を想定。N(区間)=1の時は単利で2倍となるだけだが「区切った期間ごとに利息を元金に繰り込む」複利計算によって増加率は増大を続けネイピア数e(2.718282)に収束する(自然指数関数e^1の値)。
- また「1/6の確率で1の目が出るサイコロを6個振った場合、1回も1の目が出ない確率」などを求めるベルヌーイ試行(1-1/N)^NはN=1の時の0(すなわち両方とも表のコインを振って裏が出る確率)から出発してネイピア数eの逆数1/e(0.3678794)に収束する(自然対数e^-1の値)。
弟子のレオンハルト・オイラー(Leonhard Euler, 1707年〜1783年)はさらにマクリーン変換を用いてこのe^±x=(1±x/N)^Nの式の分子に複素数θiを挿入すると求められる結果が確率から単位円上の角度に変換される事を証明。かくして有名なオイラーの公式(Euler's formula)e^θi=Cos(θ)+Sin(θi)が導出される展開を迎える。この場合にはNは(円弧がちゃんと顕現する程度に)十分大きければよよい。
オイラーの公式(1/4周分)=e^(1/2πi)=(1+1/2πi/N)^N
オイラーの公式(半周分)=e^(πi)=(1+πi/N)^N
オイラーの公式(3/4周分)=e^(3/2πi)=(1+3/2πi/N)^N
オイラーの公式(1周分)=e^(2πi)=(1+2πi/N)^N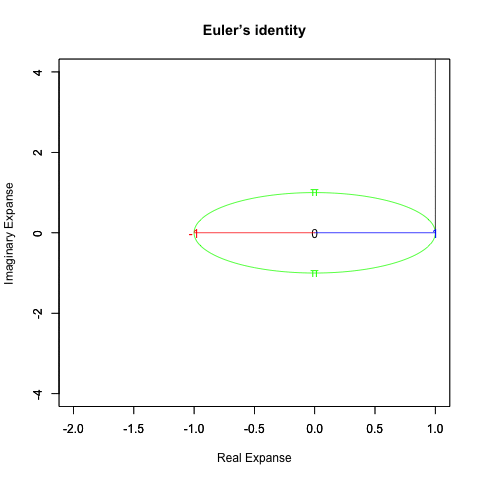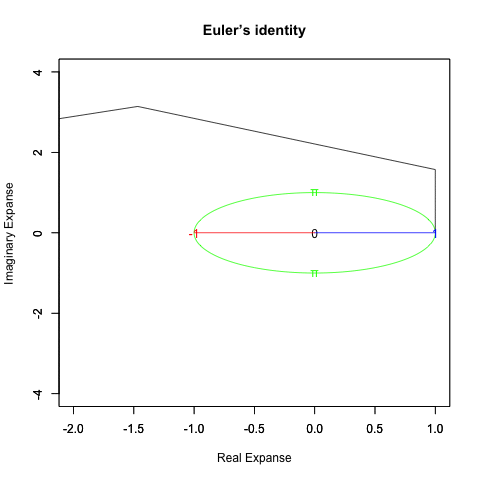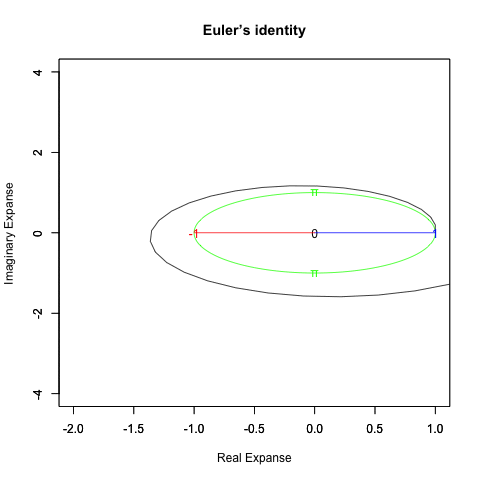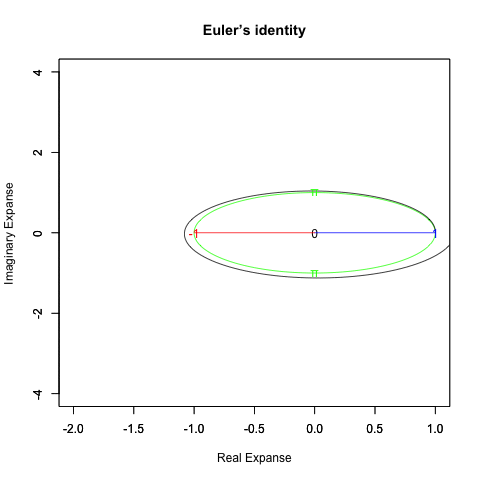
オイラーの公式(2周分)=e^(4πi)=(1+4πi/N)^N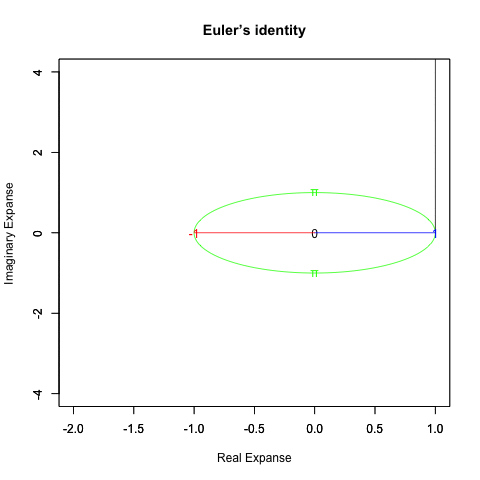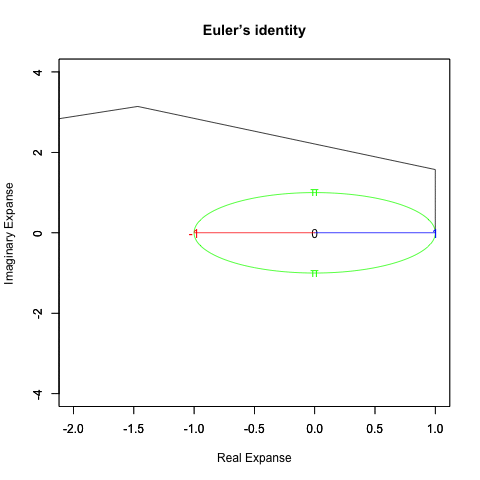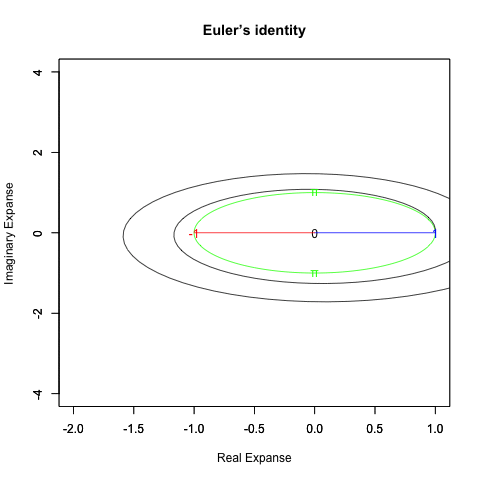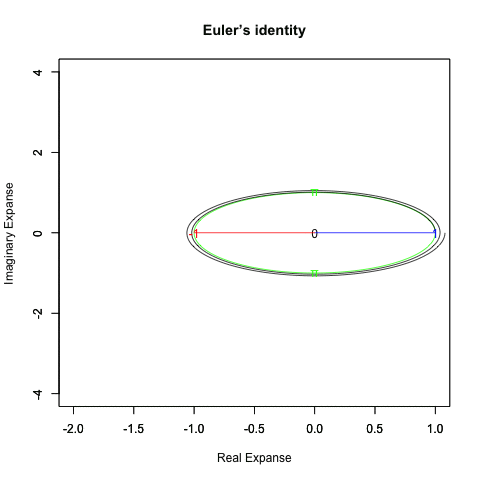
逆オイラーの公式(1/4周分)=e^(-1/2πi)=(1-1/2πi/N)^N
逆オイラーの公式(半周分)=e^(-πi)=(1-πi/N)^N
逆オイラーの公式(3/4周分)=e^(-3/2πi)=(1-3/2πi/N)^N

逆オイラーの公式(1周分)=e^(-2πi)=(1-2πi/N)^N

逆オイラーの公式(2周分)=e^(-4πi)=(1-4πi/N)^N