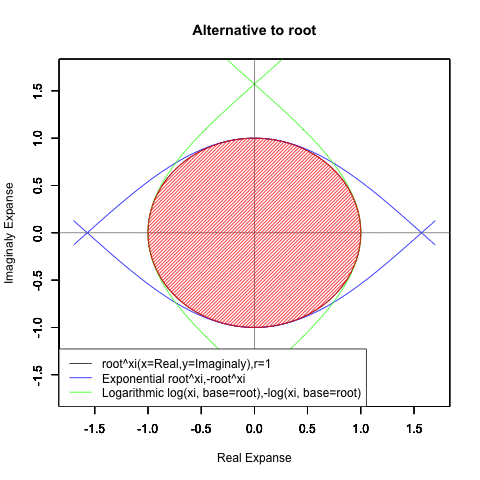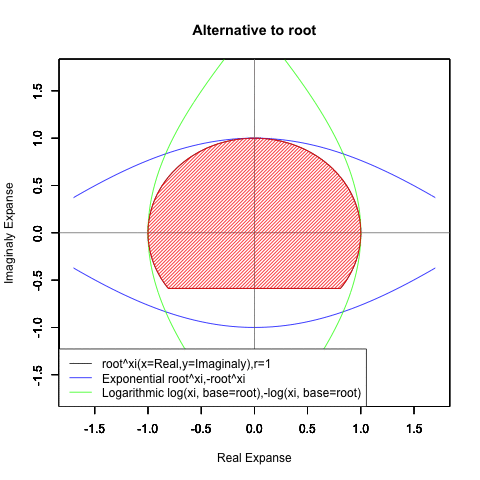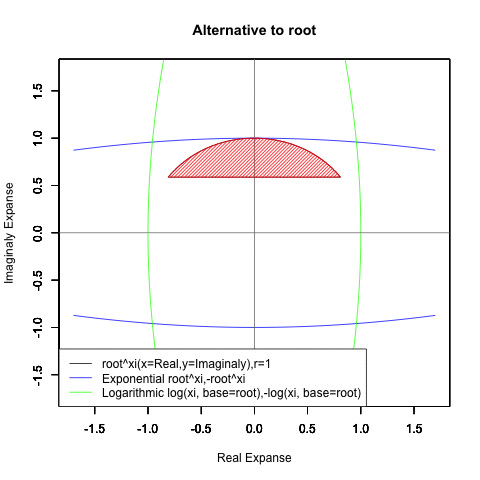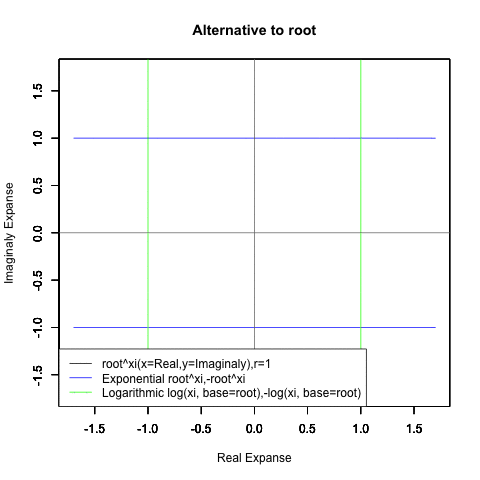
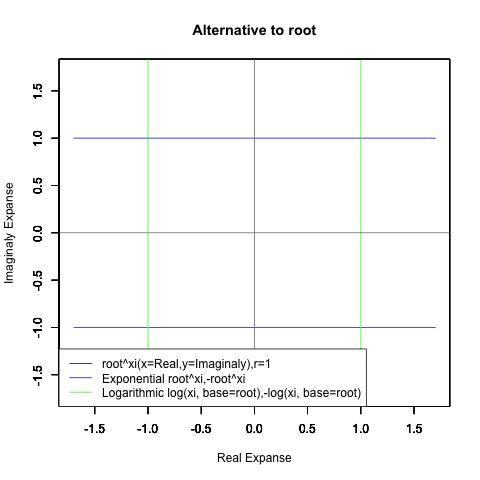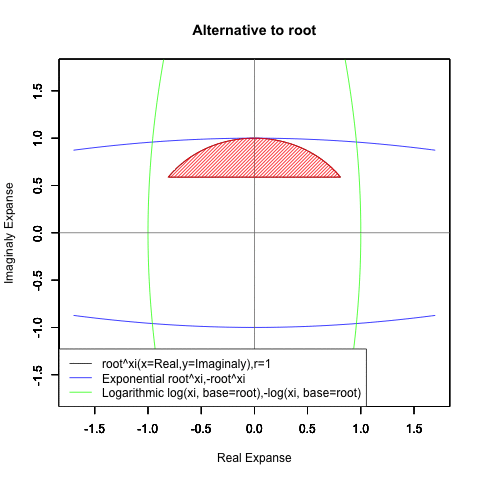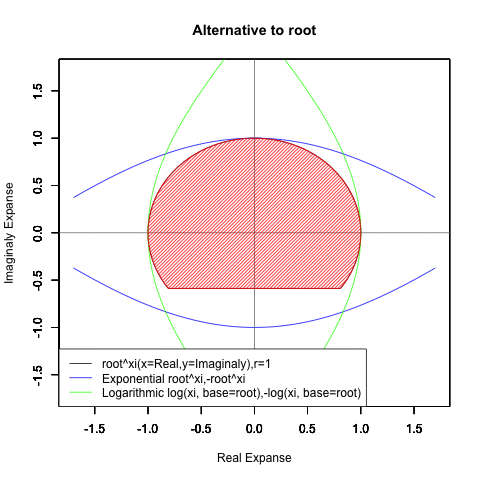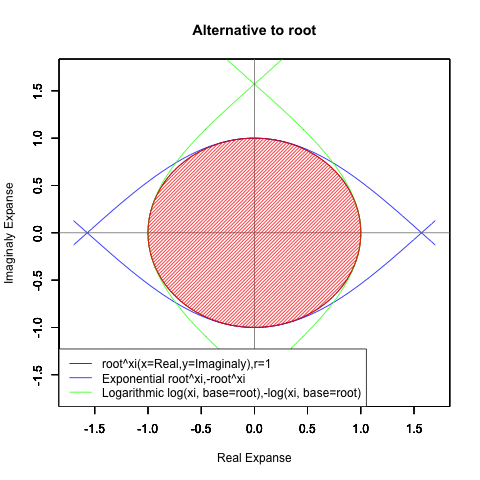
ネイピア数e(2.718282)はしばしば定数として扱われますが実際には自然指数関数e^xや自然対数関数Log(x)がそれぞれの状態においじて返す超越数の一部なのです。そしてこれらの関数は他に極限値として1/eや1を返してきます。
統計言語Rによる図示例
#ネイピア数を底とする指数関数・対数関数
f0<-function(x){exp(x)}
f1<-function(x){log(x)}
plot(f0,xlim=c(-8,8),ylim=c(-8,8),type="l",col=rgb(1,0,0), main="Exponential and logarithmic functions to base Napier number", xlab="x", ylab="y")
par(new=T)#上書き指定
plot(f1,xlim=c(-8,8),ylim=c(-1,8),col=rgb(0,0,1),main="", xlab="", ylab="")
legend("topleft", legend=c("y=e^x", "y=log(x)"), lty = c(1,1),col=c(rgb(1,0,0),rgb(0,0,1)))
ところで自然指数関数e^xや自然対数関数Log(x)のもう一つの極限値としての"1"とは一体どういう内容なんでしょうか?
①e^1=exp(1)=(1+1/N)^N=2.718282
ヤコブ・ベルヌーイ(Jakob Bernoulli、1654年〜1705年)が1683年に用いた複利計算式「(1+1/N)^N」に立脚する導出方法。
- まず「原資1を預けると1年で利息1がついて倍になる」夢の金融商品を想定する。
- これは単利のケースだが、上掲の複利計算式すなわち「区切った期間ごとに利息を元金に繰り込む」を選ぶとさらなる利息がつく。
- ただし無制限に増加し続ける訳ではなくある値、すなわちネイピア数e(2.718282)で頭打ちとなる。
これが実は増減が爆発的で「指数関数的増衰」なる表現すらある指数関数a^xの算出方法そのものなのである。
統計言語Rによる検証結果
f0<-function(N){(1+1/N)^N}
f0(0)
[1] 1
f0(1)
[1] 2
f0(2)
[1] 2.25
f0(3)
[1] 2.37037
f0(4)
[1] 2.441406
f0(5)
[1] 2.48832
f0(6)
[1] 2.521626
f0(12)
[1] 2.613035
f0(36)
[1] 2.681464
f0(64)
[1] 2.697345
f0(128)
[1] 2.707739
f0(256)
[1] 2.712992
グラフ化してみる。
#ヤコブ・ベルヌイの複利計算法に基づく算出方法
f0=function(x){(1+1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,3),lty =1,main="Natural logarithm", xlab="N", ylab="(1+1/N)^N")
#自然対数eと比較。
abline(h=exp(1))#exp(1)=2.718282...

「指数関数的増衰」…そう、実際には「増大」だけでなく「減衰」もある。指数関数a^xにのみ存在し対数関数Log(x,base=a)はどれもこれを備えない。
- a^x…一般的増大から「指数関数的増大」へ
- (1/a)^x…「指数関数的減衰」から一般的減少へ
- -a^x…「指数関数的増大」から一般的増大へ
- -(1/a)^x…一般的減少から「指数関数的減衰」へ

②e^-1=exp(-1)=(1-1/N)^N=0.3678794
一方、ベルヌーイの弟子レオンハルト・オイラー(Leonhard Euler, 1707年〜1783年)はジョン・ネイピア(John Napier, 1550年〜1617年)の対数表の底「0.9999999」と師匠ベルヌーイの考案したベルヌーイ試行の概念を組み合わせた式(1-1/N)^Nを研究。 結果としてもう一つの極限値exp(1)^-1=exp(-1)=1/exp(1)=0.3678794を求める形となった。
- 例えば1が出る確率が1/6であるサイコロを6回振って1回も1が出ない確率はどれくらいあるのだろう。ベルヌーイ試行の概念に従って(1-1/6)^6を計算すると0.334898となる。
- より一般化して(1-1/N)^Nを計算するとネイピア数e(2.718282)の逆数、すなわち1/e(0.3678794)で収束する。
ちなみにこの様に「試行を厖大に繰り返せば、出た目の平均(標本平均)が出る目の平均である 3.5 の近傍から外れる確率をいくらでも小さくできる=独立同分布に従う可積分な確率変数列の標本平均は平均に収束する」と考える極限定理(確率論・統計学における基本定理)の一種「大数の法則(英Law of Large Numbers, LLN、仏Loi des grands nombres)」のうちヤコブ・ベルヌーイが提唱したこの内容を「大数の弱法則 (WLLN: Weak Law of Large Numbers) 」という。エミール・ボレルやアンドレイ・コルモゴロフが提唱した「大数の強法則 (SLLN: Strong Law of Large Numbers) 」はさらに「同じ条件下で、n → ∞ とすればほとんど確実に(almost surely, 確率 1 で)収束する」と主張する。
統計言語Rによる検証結果
f1<-function(N){(1-1/N)^N}
f1(0)
[1] 1
f1(1)
[1] 0
f1(2)
[1] 0.25
f1(3)
[1] 0.2962963
f1(4)
[1] 0.3164062
f1(5)
[1] 0.32768
f1(6)
[1] 0.334898
f1(12)
[1] 0.3519956
f1(24)
[1] 0.3600794
f1(32)
[1] 0.3620553
f1(64)
[1] 0.3649865
f1(128)
[1] 0.3664377
グラフ化してみる。
#オイラーの「ネイピアの対数表」に基づく算出方法
f0=function(x){(1-1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,0.5),lty =1,main="Natural logarithm", xlab="N", ylab="(1-1/N)^N")
#自然対数1/eと比較。
abline(h=exp(-1))#exp(-1)=0.3678794...

③exp(0)=exp(-1)*exp(1)=*1^N=1
両者の間に横たわる(指数0、値1)e^0=1もまた一つの極限値である。
- 「(1/N)^N」を計算しても急激に0に近付く減衰曲線を描くのみ。
#オイラーの「ネイピアの対数表」に基づく算出方法
f0=function(x){(1/x)^x}
#グラフ化してみる。
plot(f0, xlim=c(0,50),ylim=c(0,0.5),lty =1,main="n-th root of 1 / n", xlab="N", ylab="(1/N)^N")
- 正解はexp(-1)*exp(1)=(1-1/N)^N*(1-1/N)^N=*2^N=1となる。
統計言語Rによる計算例
#exp(-1)*exp(1)=(1-1/N)^N*(1-1/N)^N=*3^N=1
f3<-function(N){*4^N}
f3(0)
[1] 1
f3(1)
[1] 0
f3(2)
[1] 0.5625
f3(3)
[1] 0.702332
f3(4)
[1] 0.7724762
f3(5)
[1] 0.8153727
f3(6)
[1] 0.8444876
f3(16)
[1] 0.9392981
f3(32)
[1] 0.9692184
f3(64)
[1] 0.9844946
f3(128)
[1] 0.9922177統計言語Rによるグラフ化
#exp(-1)*exp(1)=(1-1/N)^N*(1-1/N)^N=*5^N=1
f3<-function(N){*6^N}
plot(f3, xlim=c(0,50),ylim=c(0,1),lty =1,main="(1+1/N)*(1-1/N))^N", xlab="N", ylab="(1+1/N)*(1-1/N))^N")
指数関数の原点e^0=1のイメージがより明瞭になった?