一般に「三平方の定理(Three square theorem)」あるいは「ピタゴラスの定理(Pythagorean theorem)」として知られるX^2+Y^2=Z^2の式、すなわち単位円(Unit Circle、半径1の円弧)上ではx^2+y^2=1、 単位球面(Unit Circle、半径1の円弧)上ではx^2+y^2+z^2=1、となる定理について。しばしばYの値をXで求める関数に変換されたY=sqrt(1-X^2)の形式でも用いられます。

三平方の定理の証明
①直角三角形を4個集めると正方形が出来る。
②大きな正方形の面積Sは一辺が{a,ab}={b,bc}={c,cd}={d,da}(Aとする)で、かつ{ab,b}+{bc,c}+{cd,c}={da,a}(Bとする)にして{a,ab}+{ab,b}={b,bc}+{bc+b}={c,cd}+{cd,d}={d,da}+{da,a}なので
S=(A+B)^2
③またSは一辺が{ab,bc}={bc,cd}={cd,da}={da=ab}(Cとする)の正方形とABの直角三角形4つの和でもあるので
S=C^2+4*1/2*A*B
④よって
A^2+2AB+B^2=C^2+2AB
⑤これを整理すると
A^2+B^2=C^2
a^2+b^2=c^2からsinθ^2+cosθ^2=1へ
ここに登場する直角三角形ABCは(プログラム中での扱いを見ても分かる様に)以下とも置ける。
a=cos(θ)
b=sin(θ)
c=1
よって同時に任意の角度θに対して以下が成立。
cos(θ)^2+sin(θ)^2=1

統計言語Rによる作図
f0<-function(x){cos(x)^2}
plot(f0,col=rgb(0,0,1),xlim=c(0,2*pi),ylim=c(0,1),main="Three square theorem",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){sin(x)^2}
plot(f1,col=rgb(0,1,0),xlim=c(0,2*pi),ylim=c(0,1),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)^2+sin(x)^2}
plot(f2,,col=rgb(1,0,0),xlim=c(0,2*pi),ylim=c(0,1),main="",xlab="",ylab="")
legend("bottomright", legend=c("y=cos(θ)^2","y=sin(θ)^2","y=cos(θ)^2+sin(θ)^2"), lty=c(1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0)))
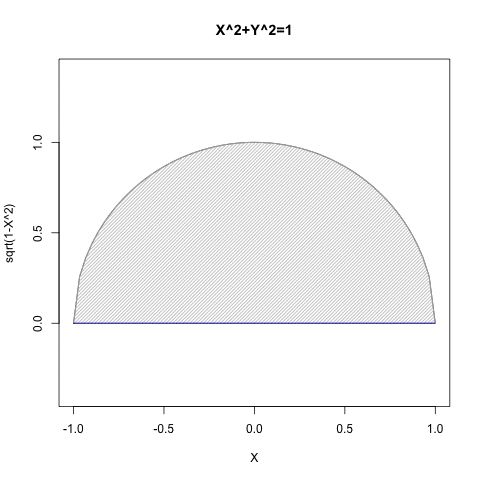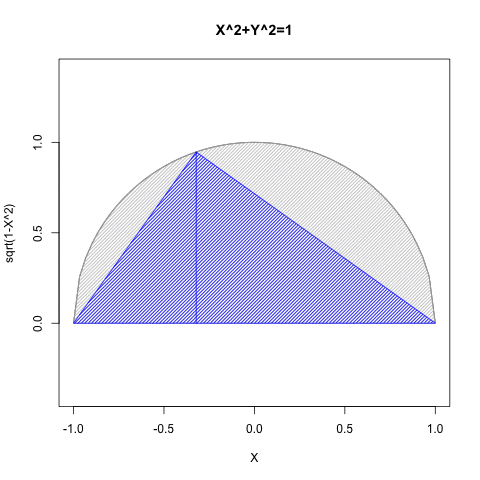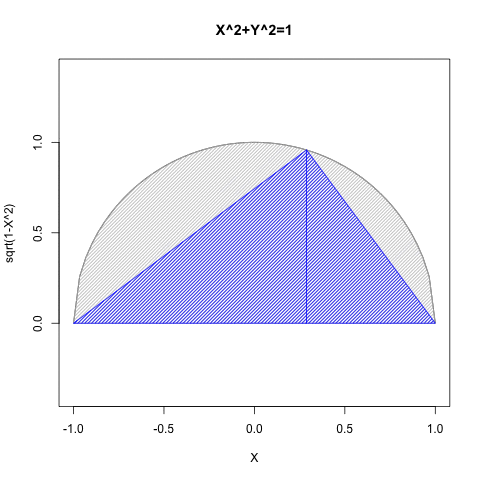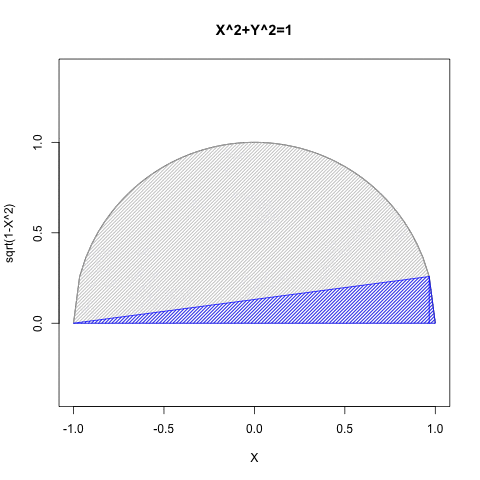
①一般にこの定理は「半円しか描けない」「従ってY=sqrt(1-X^2)の式とY=-sqrt(1-X^2)の式のセットで運用するもの」と考えられている。
統計言語Rによるプログラミング例
#CFS=Circle Function Single
CFS<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2)")#塗りつぶし(背景)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色#塗りつぶし(三角)
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#線追加(三角)segments(cx[Radian],cy[Radian],cx[Radian],0,col=c(100,100,100))
}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CFS(i)
}
}, interval = 0.1, movie.name = "CFS01.gif")
統計言語Rによるプログラミング例
#CFD=Circle Function Double
CFD<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="X",ylab="sqrt(1-X^2) &-sqrt(1-X^2) ")par(new=T)#上書き指定
plot(cx,-1*cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
#塗りつぶし(上背景)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(下背景)polygon(cx, #x
-cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色#塗りつぶし(上三角)
polygon(c(-1,cx[Radian],1), #x
c(0,cy[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色#塗りつぶし(下三角)
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(1,cx1[Radian],-1), #x
c(0,cy1[Radian],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色#線追加(三角)
segments(cx[Radian],cy[Radian],cx[Radian],0,col=rgb(0,0,1))
segments(cx1[Radian],cy1[Radian],cx1[Radian],0,col=rgb(1,0,0))
#凡例
legend("bottomright", legend=c("sqrt(1-X^2)","-sqrt(1-X^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CFD(i)
}
}, interval = 0.1, movie.name = "CFD01.gif")

②「半円しか描けない」は、正確には以下の状態を指す。
- Xの関数としてYを求める場合には第一象限(X=>0かつY=>0)と第二象限(X=<0かつY=>0)の場合のみ有効。
- Yの関数としてXを求める場合には第一象限(X=>0かつY=>0)と第四象限(Y=<0かつX=>0)の場合み有効。
統計言語Rによるプログラミング例
#CFS90Sift=Circle Function Single 90Sift
CFS90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",main="X^2+Y^2=1",xlab="sqrt(1-Y^2)",ylab="Y")#塗りつぶし(背景)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色#塗りつぶし(三角)
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#線追加(三角)
segments(cy[Radian],cx[Radian],0,cx[Radian],col=c(100,100,100))}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CFS90Sift(i)
}
}, interval = 0.1, movie.name = "CFS90Sift01.gif")
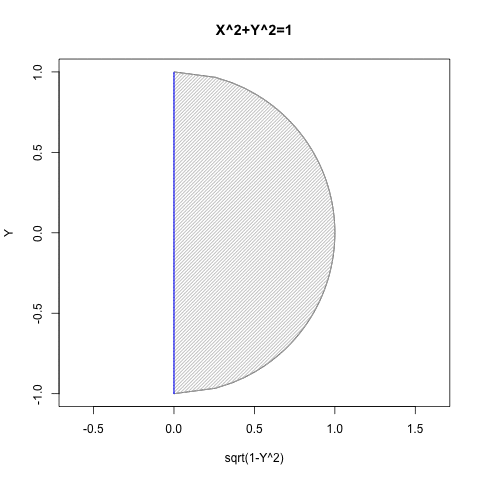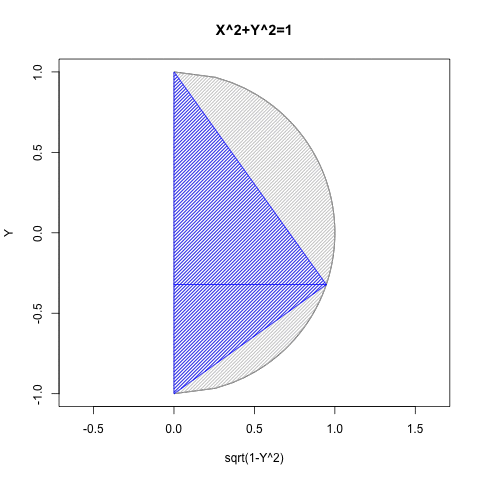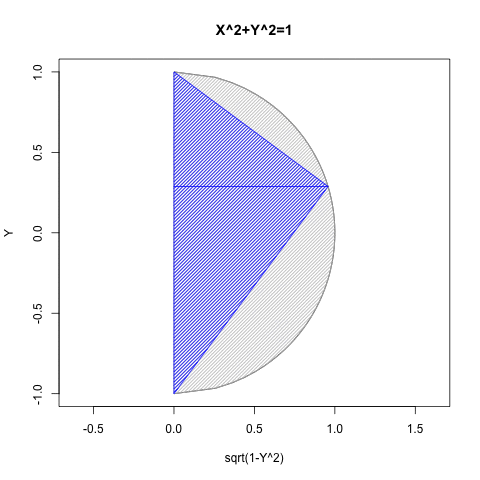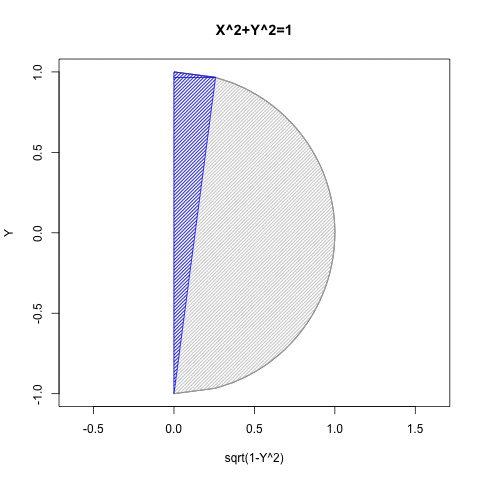
統計言語Rによるプログラミング例
#CFD90Sift=Circle Function Double 90Sift
CFD90Sift<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2) &-sqrt(1-Y^2)",ylab="Y")par(new=T)#上書き指定
plot(cy*-1,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
#塗りつぶし(上背景)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(下背景)polygon(-cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色#塗りつぶし(上三角)
polygon(c(0,cy[Radian],0), #x
c(-1,cx[Radian],1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色#塗りつぶし(下三角)
cx1<-rev(cx)
cy1<-rev(cy)*-1
polygon(c(0,cy1[Radian],0), #x
c(1,cx1[Radian],-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色#線追加(三角)
segments(cy[Radian],cx[Radian],0,cx[Radian],col=rgb(0,0,1))
segments(cy1[Radian],cx1[Radian],0,cx1[Radian],col=rgb(1,0,0))#凡例
legend("bottomright", legend=c("sqrt(1-Y^2)","-sqrt(1-Y^2)"), lty=c(1,1), col=c(rgb(0,0,1),rgb(1,0,0)))}
#アニメーション
library("animation")
Time_Code=seq(1,59, length=30)
saveGIF({
for (i in Time_Code){
CFD90Sift(i)
}
}, interval = 0.1, movie.name = "CFD90Sift01.gif")

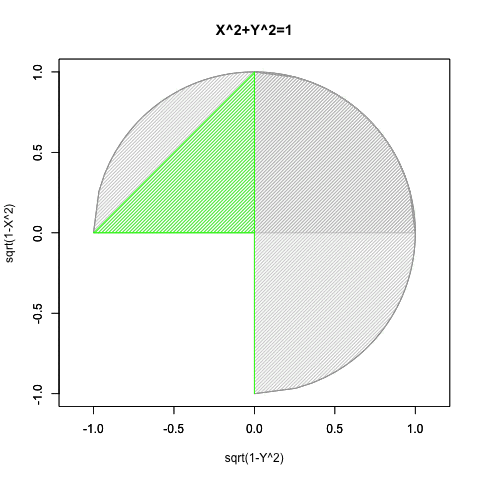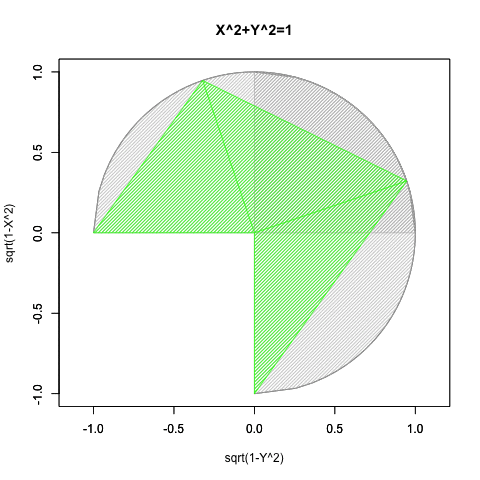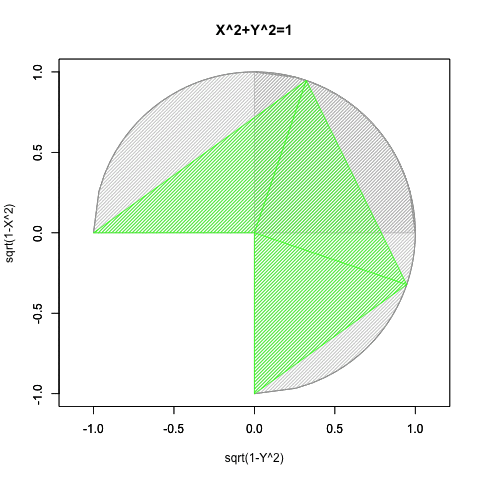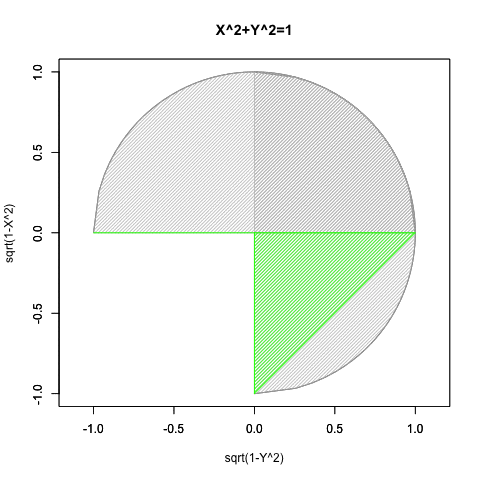
③要するにこのアプローチによっては手が出せないのは、第三象限(X=<0かつY=<0)のみという事になる。
統計言語Rによるプログラミング例
#CFC=Circle Function Closs
CFC<-function(Radian){
cx<-seq(-1,1,length=60)
f0<-function(x) sqrt(1-x^2)
cy<-f0(cx)
plot(cx,cy,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="X^2+Y^2=1",xlab="sqrt(1-Y^2)",ylab="sqrt(1-X^2)")par(new=T)#上書き指定
plot(cy,cx,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="",xlab="",ylab="")
#塗りつぶし(X軸)
polygon(cx, #x
cy, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色#塗りつぶし(Y軸)
polygon(cy, #x
cx, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色#塗りつぶし(三角)
cx1<-rev(cx)
cy1<-rev(cy)
polygon(c(-1,cx[Radian],cy1[Radian],0,0,-1), #x
c(0,cy[Radian],cx1[Radian],-1,0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色#線追加(三角)
segments(cx[Radian],cy[Radian],0,0,col=rgb(0,1,0))
segments(cy1[Radian],cx1[Radian],0,0,col=rgb(0,1,0))}
#アニメーション
library("animation")
Time_Code=c(1:60)
saveGIF({
for (i in Time_Code){
CFC(i)
}
}, interval = 0.1, movie.name = "CFC01.gif")
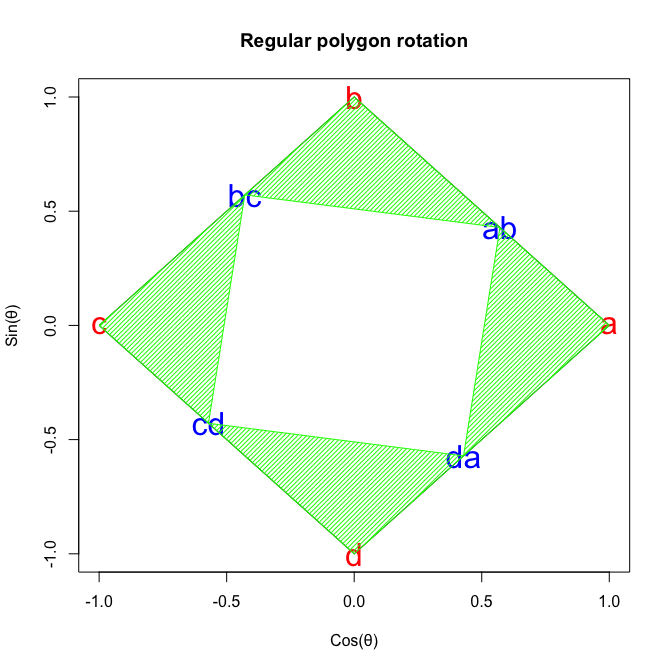
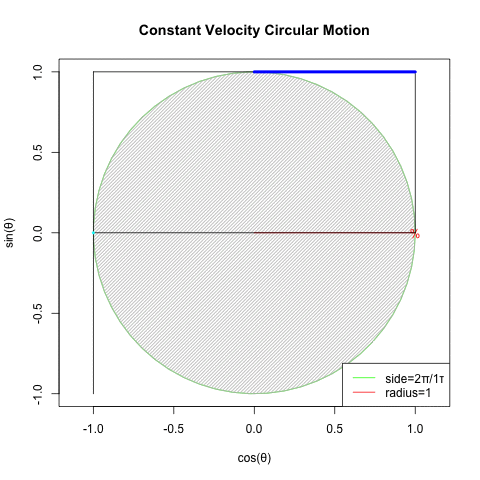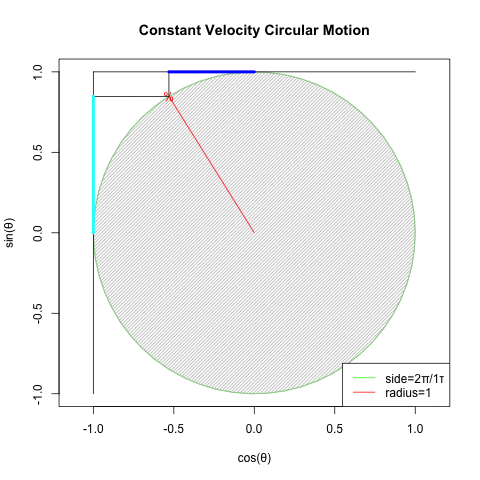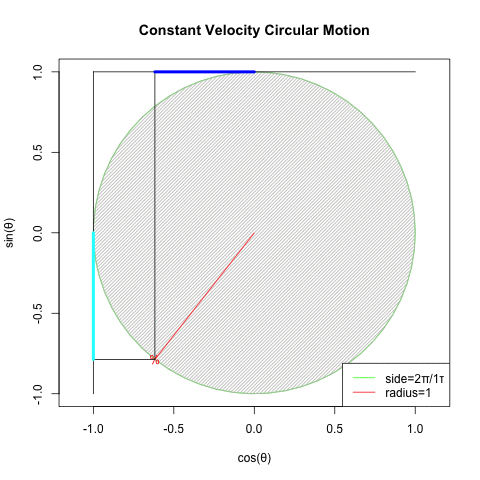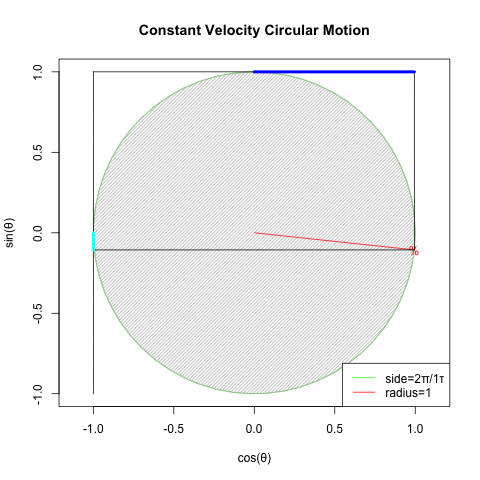
④オイラーの公式(Euler's formula)Cos(θ)+Sin(θ)iの式や、物理学上における等速円運動解析(Constant velocity circular motion)の概念は、この制約を超越した。数学史上は18世紀前後の話となる。
統計言語Rによる「正方形の完全回転」実現例
#FRoS=Full Rotation of Square
FRoS<-function(Radian){c0<-seq(0,2*pi,length=60)
cx0<-cos(c0)
cy0<-sin(c0)
plot(cx0,cy0,asp=1,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Full Rotation of Square",xlab="cos(θ)",ylab="sin(θ)")par(new=T) #上書き
c1<-seq(0,2*pi,length=5)+Radian
cx1<-cos(c1)
cy1<-sin(c1)
plot(cx1,cy1,asp=1,type="l",xlim=c(-1,1), ylim=c(-1,1), main="",xlab="",ylab="")#塗りつぶし(円)
polygon(cx0, #x
cy0, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=c(200,200,200)) #塗りつぶす色
#塗りつぶし(四角)
polygon(cx1, #x
cy1, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色}
#アニメーション
library("animation")
Time_Code=seq(0,pi/2, length=15)
saveGIF({
for (i in Time_Code){
FRoS(i)
}
}, interval = 0.1, movie.name = "FRoS01.gif")
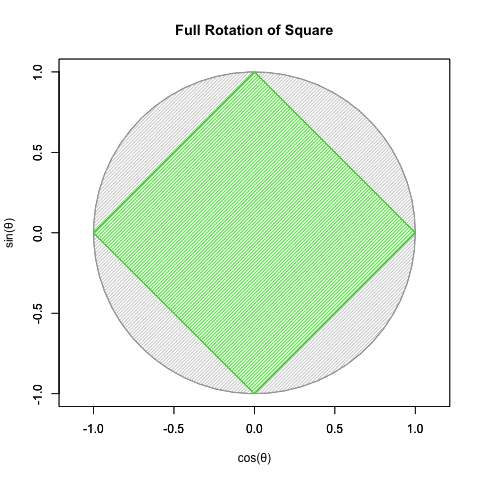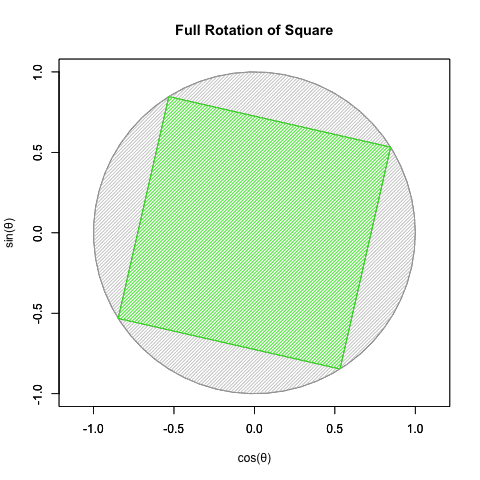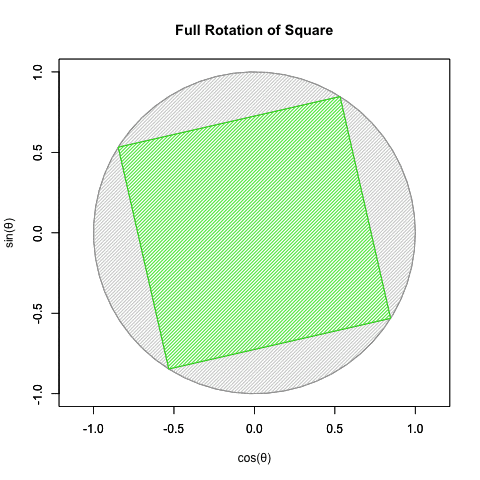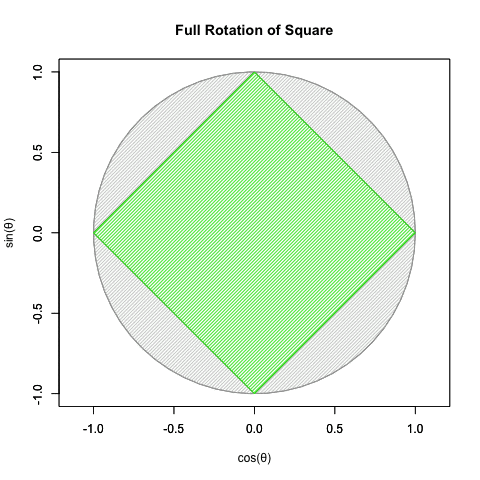
統計言語Rによるオイラーの公式(Euler's formula)Cos(θ)+Sin(θ)i実現例

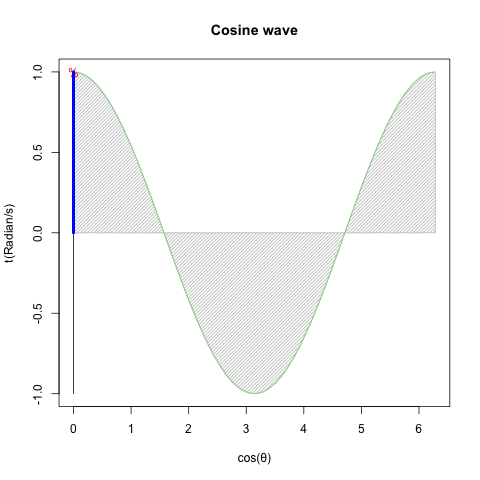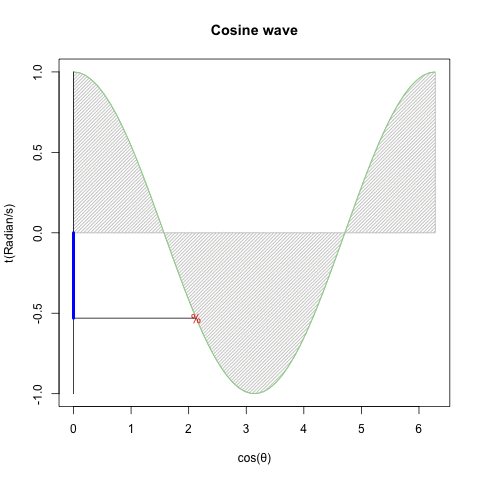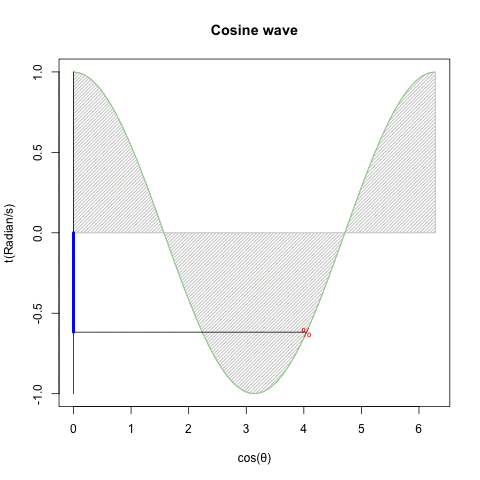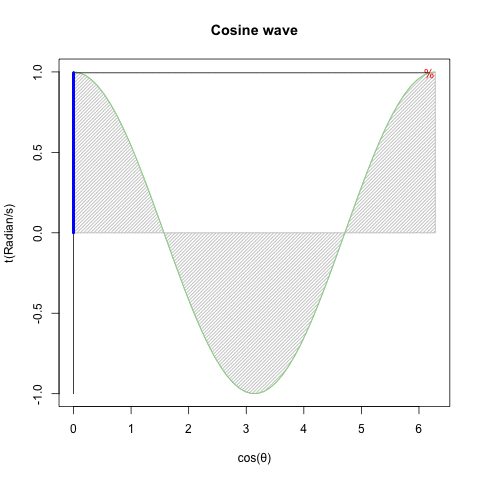

⑤かかる三角関数(Trigonometric function)上のパラダイムシフトに際し、(物理界でなく)数学界のみで虚数(Imaginary Number)や複素数(Complex Number)といった新概念の導入が不可避となった。要するに鍵となったのは「振動」についての解釈能力差…
数列の極限は,
- 1…(有限の値に)収束する。
- 2A…正の無限大に発散する。
- 2B…負の無限大に発散する。
- 3…振動する。
のいずれかである。2と3の場合をいずれも発散すると言う。
例題5「数列 An=(−1)^n の極限を調べよ」の解答
Anは−1 と 1 をひたすら交互に繰り返す。収束,正の無限大に発散,負の無限大に発散,のいずれにも当てはまらないので振動に分類される。

ところで所謂「ピタゴラスの定理」は対象数列に「曲率」を付与します。対象が線分の場合は所謂「半円」しか構成し得ませんが「基本円柱(Basic Cylinder)」だと球面が構成されるのです。