実はオイラーの公式cos(θ)+sin(θ)iとは多角形方程式Cos(θ)+Cos(θ-π/NoC)i(NoC=Number of Corners=角数)の特殊解に過ぎず、しかも後者はその成立を「正2角形以下」に限定してしまうので「三角形以上の成立しか許さない」平面幾何学(Plane geometry)を代表するユークリッド幾何学(Euclidean geometry)の世界と直接の関わりを備えていません。

- 多角形方程式Cos(θ)+Cos(θ-π/NoC)iにおける1角形(Hanagon)から2角形(Hanagon)を経て円そのもの(Circle itself)に至る展開。1角形(Hanagon)から2角形(Digon)にかけて「比較的素早く」90度旋回した後、残り90度を円そのもの(Circle itself)に向けて角数を無限大に収束させる形でゆっくり消化(あまりにゆっくりなので画像は途中から加速)。


- 次は真逆の方向に該当する多角形方程式Cos(θ)+Cos(θ-π/NoC)iにおける1角形(Hanagon)以下の展開。2角形(Hanagon)から始まる回転周期を2/(2N+1)の式に従って短縮させつつ無限小に収束させていく。

いわゆる一つのパルサー(pulsar=中性子星)爆発状態?
そう、多角形方程式(Poligons equattion)は、正方形(Square)におけるオイラーの公式cos(θ)+sin(θ)iの成立を「原則として」認めていないのです。
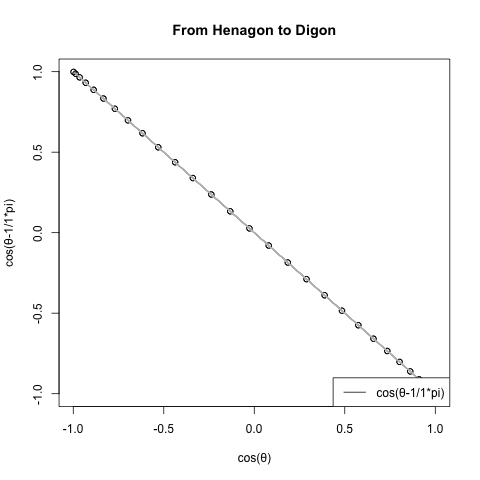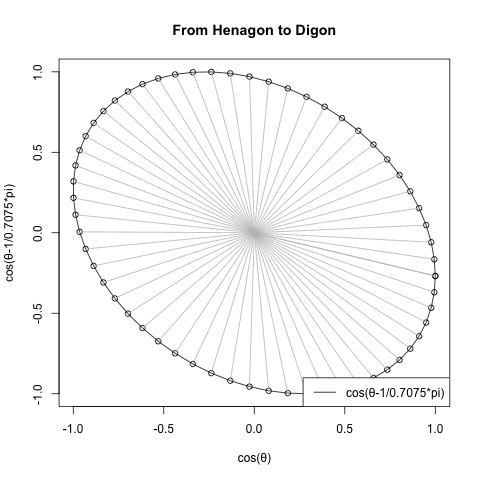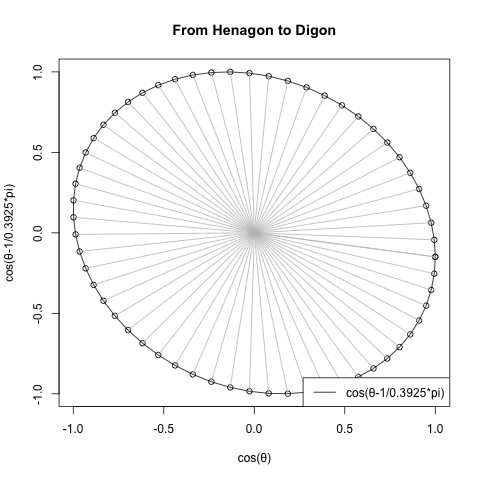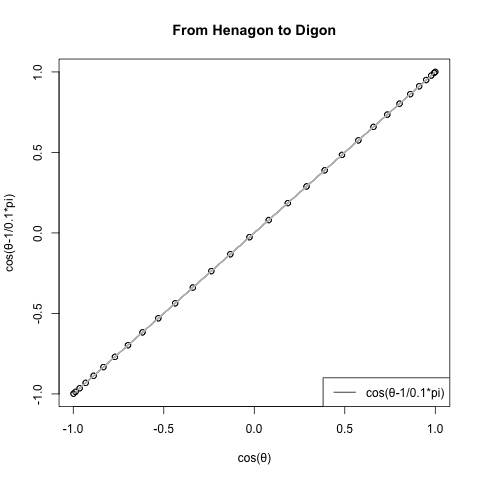
統計言語Rによるプログラミング例(正方形=四角形の場合、真円にならない)、
#FHtD=1角形から2角形へ(From Henagon to Digon)
#Noc=角数(Number of corners)
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)#中心からの補助線
cx0<-rep(0, length=length(cx))
cy0<-rep(0, length=length(cy))
segments(cx0, cy0, cx, cy,col=c(200,200,200))#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}FHtD(4)

そして両者を結ぶのが、とりあえずこのサイトでは「辺長サンプリング効果(Side length sampling effect)」と呼ぶ事にした「N角形は多角形方程式の周期を1/Nし、その先頭部分だけをN回繰り返す」現象となってくる訳です。

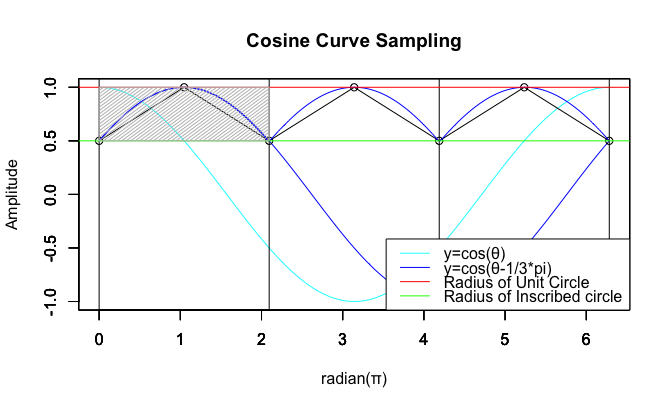




この現象が正方形でだけ「直交座標系(Rectangular coordinate system / Orthogonal coordinate system)の座標操作手順」と重なる形で遂行される訳です。それでは実際に順を追って見ていきましょう。「最初の1/4周期を4回繰り返す」しかも90度ローテーションしながら。それは要するに以下の様な展開を指すのですね。

統計言語Rによる「サンプリング元」の作図
f0<-function(x){cos(x)}
plot(f0,col=rgb(0,0,1),xlim=c(0,2*pi),ylim=c(-1.5,1.5),main="Three square theorem",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){sin(x)}
plot(f1,col=rgb(0,1,0),xlim=c(0,2*pi),ylim=c(-1.5,1.5),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)+sin(x)}
plot(f2,col=rgb(1,0,0),xlim=c(0,2*pi),ylim=c(-1.5,1.5),main="",xlab="",ylab="")
par(new=T) #上書き
f3<-function(x){cos(x)*sin(x)}
plot(f3,col=c(125,125,125),xlim=c(0,2*pi),ylim=c(-1.5,1.5),main="",xlab="",ylab="")
par(new=T) #上書き
f4<-function(x){cos(x)^2+sin(x)^2}
plot(f4,col=rgb(0,0,0),xlim=c(0,2*pi),ylim=c(-1.5,1.5),main="",xlab="",ylab="")abline(v = pi/2)
legend("bottomright", legend=c("y=cos(θ)","y=sin(θ)","y=cos(θ)+sin(θ)","y=cos(θ)*sin(θ)","y=cos(θ)^2*sin(θ)^2"), lty=c(1,1,1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0),c(125,125,125),rgb(0,0,0)))
統計言語Rによる作図(0/4回転)

rad<-seq(0,pi/2,length=60)
f0<-function(x){cos(x)}
f0_y<-f0(rad)
plot(rad,f0_y,type="l",col=rgb(0,0,1),xlim=c(0,pi/2),ylim=c(0,sqrt(2)),main="Side length sampling effect(0/4 Rotation)",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){sin(x)}
f1_y<-f1(rad)
plot(rad,f1_y,type="l",col=rgb(0,1,0),xlim=c(0,pi/2),ylim=c(0,sqrt(2)),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)+sin(x)}
f2_y<-f2(rad)
plot(rad,f2_y,type="l",col=rgb(1,0,0),xlim=c(0,pi/2),ylim=c(0,sqrt(2)),main="",xlab="",ylab="")
par(new=T) #上書き
f3<-function(x){cos(x)*sin(x)}
f3_y<-f3(rad)
plot(rad,f3_y,type="l",col=rgb(0,1,1),xlim=c(0,pi/2),ylim=c(0,sqrt(2)),main="",xlab="",ylab="")
par(new=T) #上書き
f4<-function(x){sqrt(cos(x)^2+sin(x)^2)}
f4_y<-f4(rad)
plot(rad,f4_y,type="l",col=rgb(0,0,0),xlim=c(0,pi/2),ylim=c(0,sqrt(2)),main="",xlab="",ylab="")
legend("bottomright", legend=c("y=cos(θ)","y=sin(θ)","y=cos(θ)+sin(θ)","y=cos(θ)*sin(θ)","y=(sqrt(cos(θ)+sin(θ)^2)"), lty=c(1,1,1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0),rgb(0,1,1),rgb(0,0,0)))
統計言語Rによる作図(1/4回転)

rad<-seq(0,pi/2,length=60)
f0<-function(x){cos(x)}
f0_y<-f0(rad)
plot(-1*f0_y,rad,type="l",col=rgb(0,0,1),xlim=c(-1*sqrt(2),0),ylim=c(0,pi/2),main="Side length sampling effect(1/4 Lotation)",xlab="Amplitude",ylab="radian(π)")
par(new=T) #上書き
f1<-function(x){sin(x)}
f1_y<-f1(rad)
plot(-1*f1_y,rad,type="l",col=rgb(0,1,0),xlim=c(-1*sqrt(2),0),ylim=c(0,pi/2),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)+sin(x)}
f2_y<-f2(rad)
plot(-1*f2_y,rad,type="l",col=rgb(1,0,0),xlim=c(-1*sqrt(2),0),ylim=c(0,pi/2),main="",xlab="",ylab="")
par(new=T) #上書き
f3<-function(x){cos(x)*sin(x)}
f3_y<-f3(rad)
plot(-1*f3_y,rad,type="l",col=rgb(0,1,1),xlim=c(-1*sqrt(2),0),ylim=c(0,pi/2),main="",xlab="",ylab="")
par(new=T) #上書き
f4<-function(x){sqrt(cos(x)^2+sin(x)^2)}
f4_y<-f4(rad)
plot(-1*f4_y,rad,type="l",col=rgb(0,0,0),xlim=c(-1*sqrt(2),0),ylim=c(0,pi/2),main="",xlab="",ylab="")
legend("bottomright", legend=c("y=cos(θ)","y=sin(θ)","y=cos(θ)+sin(θ)","y=cos(θ)*sin(θ)","y=(sqrt(cos(θ)+sin(θ)^2)"), lty=c(1,1,1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0),rgb(0,1,1),rgb(0,0,0)))
統計言語Rによる作図(2/4回転)

rad<-seq(0,pi/2,length=60)
f0<-function(x){cos(x)}
f0_y<-f0(rad)
plot(rad,f0_y*-1,type="l",col=rgb(0,0,1),xlim=c(0,pi/2),ylim=c(-1*sqrt(2),0),main="Side length sampling effect(2/4 Rotation)",xlab="radian(π)",ylab="Amplitude")
par(new=T) #上書き
f1<-function(x){sin(x)}
f1_y<-f1(rad)
plot(rad,f1_y*-1,type="l",col=rgb(0,1,0),xlim=c(0,pi/2),ylim=c(-1*sqrt(2),0),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)+sin(x)}
f2_y<-f2(rad)
plot(rad,f2_y*-1,type="l",col=rgb(1,0,0),xlim=c(0,pi/2),ylim=c(-1*sqrt(2),0),main="",xlab="",ylab="")
par(new=T) #上書き
f3<-function(x){cos(x)*sin(x)}
f3_y<-f3(rad)
plot(rad,f3_y*-1,type="l",col=rgb(0,1,1),xlim=c(0,pi/2),ylim=c(-1*sqrt(2),0),main="",xlab="",ylab="")
par(new=T) #上書き
f4<-function(x){sqrt(cos(x)^2+sin(x)^2)}
f4_y<-f4(rad)
plot(rad,f4_y*-1,type="l",col=rgb(0,0,0),xlim=c(0,pi/2),ylim=c(-1*sqrt(2),0),main="",xlab="",ylab="")
legend("bottomright", legend=c("y=cos(θ)","y=sin(θ)","y=cos(θ)+sin(θ)","y=cos(θ)*sin(θ)","y=(sqrt(cos(θ)+sin(θ)^2)"), lty=c(1,1,1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0),rgb(0,1,1),rgb(0,0,0)))
統計言語Rによる作図(3/4回転)

rad<-seq(0,pi/2,length=60)
f0<-function(x){cos(x)}
f0_y<-f0(rad)
plot(f0_y,rad,type="l",col=rgb(0,0,1),xlim=c(0,sqrt(2)),ylim=c(0,pi/2),main="Side length sampling effect(3/4 Lotation)",xlab="Amplitude",ylab="radian(π)")
par(new=T) #上書き
f1<-function(x){sin(x)}
f1_y<-f1(rad)
plot(f1_y,rad,type="l",col=rgb(0,1,0),xlim=c(0,sqrt(2)),ylim=c(0,pi/2),main="",xlab="",ylab="")
par(new=T) #上書き
f2<-function(x){cos(x)+sin(x)}
f2_y<-f2(rad)
plot(f2_y,rad,type="l",col=rgb(1,0,0),xlim=c(0,sqrt(2)),ylim=c(0,pi/2),main="",xlab="",ylab="")
par(new=T) #上書き
f3<-function(x){cos(x)*sin(x)}
f3_y<-f3(rad)
plot(f3_y,rad,type="l",col=rgb(0,1,1),xlim=c(0,sqrt(2)),ylim=c(0,pi/2),main="",xlab="",ylab="")
par(new=T) #上書き
f4<-function(x){sqrt(cos(x)^2+sin(x)^2)}
f4_y<-f4(rad)
plot(f4_y,rad,type="l",col=rgb(0,0,0),xlim=c(0,sqrt(2)),ylim=c(0,pi/2),main="",xlab="",ylab="")
legend("bottomright", legend=c("y=cos(θ)","y=sin(θ)","y=cos(θ)+sin(θ)","y=cos(θ)*sin(θ)","y=(sqrt(cos(θ)+sin(θ)^2)"), lty=c(1,1,1,1,1), col=c(rgb(0,0,1),rgb(0,1,0),rgb(1,0,0),rgb(0,1,1),rgb(0,0,0)))
ただし三角関数は90度ローテーションする都度、呼び名が変わる訳で、その過程を記したのが「三角関数の微分」一覧という訳です。
- Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)→Cos(θ)
- Sin(θ)→Cos(θ)→-Sin(θ)→-Cos(θ)→Sin(θ)
そのまま連続して作図すると、あら不思議…
統計言語Rによる作図(円弧の合成)
c0<-seq(0,pi/2,length=30)
cx=c(cos(c0),sin(-c0),-cos(c0),-sin(-c0))
cy=c(sin(c0),cos(-c0),-sin(c0),-cos(-c0))
plot(cx,cy,asp=1,type="l",main="Synthesis of circular functions",xlab="x",ylab="y")
#cos(θ) & sin(θ)
polygon(c(0,cx[1:30],0), #x
c(0,cy[1:30],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色#sin(-θ) & cos(-θ)
polygon(c(0,cx[31:60],0), #x
c(0,cy[31:60],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色#-cos(θ) & -sin(θ)
polygon(c(0,cx[61:90],0), #x
c(0,cy[61:90],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色#-sin(-θ) & -cos(-θ)
polygon(c(0,cx[91:120],0), #x
c(0,cy[91:120],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,1,0)) #塗りつぶす色
#凡例
legend("bottomright", legend=c("x=cos(θ),y=sin(θ)","x=-sin(θ),y=cos(θ)","x=-cos(θ),y=-sin(θ)","x=sin(θ),y=-cos(θ)"), lty=c(1,1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1),rgb(1,1,0)))

そう、90度=あるいはπ/2Radianあるいは1/4τ(タウ)単位で4分割すると、各切片の各軸でx軸の符号を逆転させる(あるいはY=0を軸に180度回転させる)操作とy軸の符号を逆転させる(あるいはx=0を軸に180度回転させる)操作が重ねられるのです。
統計言語Rによる作図(Cos波とSin波の合成)
c1<-seq(0,2*pi,length=120)
#x=-sin(θ),y=cos(θ)
plot(c1[1:30],cx[1:30],type="l",col=rgb(1,0,0),xlim=c(0,2*pi),ylim=c(-1,1),main="Synthesis of circular functions",xlab="x",ylab="y")
par(new=T)
plot(c1[1:30],cy[1:30],type="l",col=rgb(0,1,0),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)
#x=-sin(θ),y=cos(θ)
plot(c1[31:60],cx[31:60],type="l",col=rgb(1,0,1),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)
plot(c1[31:60],cy[31:60],type="l",col=rgb(1,0,0),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)
##-cos(θ) & -sin(θ)
plot(c1[61:90],cx[61:90],type="l",col=rgb(0,0,1),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)
plot(c1[61:90],cy[61:90],type="l",col=rgb(1,0,1),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)
#x=sin(θ),y=-cos(θ)
plot(c1[91:120],cx[91:120],type="l",col=rgb(0,1,0),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
par(new=T)
plot(c1[91:120],cy[91:120],type="l",col=rgb(0,0,1),xlim=c(0,2*pi),ylim=c(-1,1),main="",xlab="",ylab="")
#補助線
abline(v=0,col=c(200,200,200))
abline(v=pi/2,col=c(200,200,200))
abline(v=pi,col=c(200,200,200))
abline(v=3*pi/2,col=c(200,200,200))
abline(v=2*pi,col=c(200,200,200))#凡例
legend("bottomright", legend=c("cos(θ)","sin(θ)","-cos(θ)","-sin(θ)"), lty=c(1,1,1,1), col=c(rgb(1,0,0),rgb(0,1,0),rgb(0,0,1),rgb(1,0,1)))

全ての発端は以下の(単位円上は内接多角形の各辺長が1からsqrt(2)の間を往復する)動作が波形的には「多角形の角数=4」すなわち角度90度=π/2Radian=τ/4の時のCos(θ)+Sin(θ)のそれであり、かつ周期360度=2π=1τの1/4を(角度90度=π/2Radian=τ/4の時の座標転換を含みつつ)4回繰り返す時に現れるそれでもある事。

実はこれ(オイラーの公式の証明に用いられた)高階微積分の応用たるテイラー級数(Taylor series)/マクローリン級数 (Maclaurin series)による近似過程にかなり合致する考え方です。
当時はまだ複素平面(Complex plane)の概念まで至っておらず、その次元ではこのアプローチによってはちゃんと円が描かれなかったりもするのですが…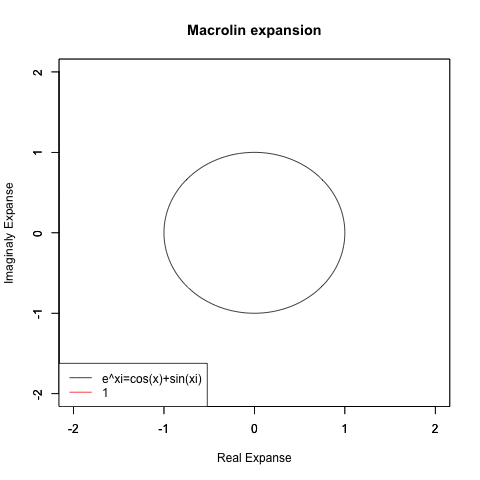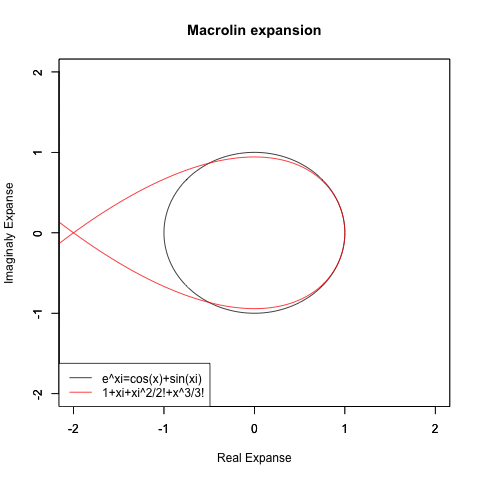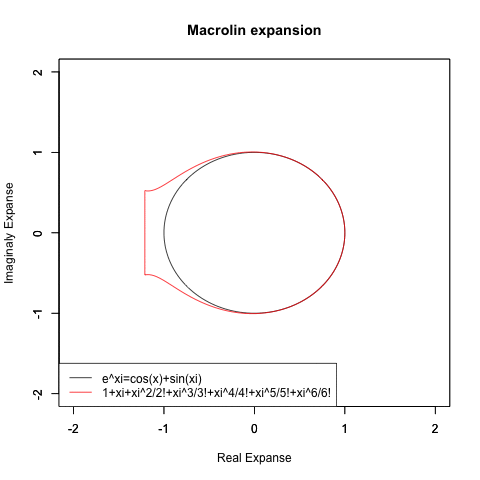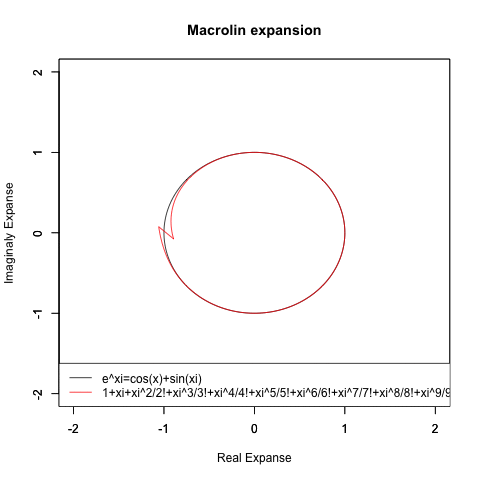
とにかくこの操作によっても原点に戻れる、すなわち「90度ローテーションしながら最初の1/4周期を4回繰り返す」辺長サンプリング効果(Side length sampling effect)によっても多角形方程式Cos(θ)+Cos(θ-π/NoC)i(NoC=Number of Corners=角数)においてオイラーの公式cos(θ)+sin(θ)iが(部分的とはいえ)満たされる条件が成立する事が確められた事こそが「人類にとっては(原義では絶対に手が届かない筈の「認識の範囲外を跳梁する絶対他者」に手が届いた)偉大な一歩の一つ」となったのです。

「部分的には」? そう、このアプローチの限界は、いわゆる「(次元軸が0を通過する際に次元自由度が一つ減る)ジンバルロック問題」において露呈するのです。


正二角形(Digon)の世界でにおいて単位球面(Unit sphere/Unit globe)上に想定されるのは以下の2点。
- 北極(Arctic)=球表面上における「観測始点」。極座標系(polar coordinates system)における「距離1、角度0度/360度あるいは0Radian/2πRadianあるいは0τ=1τ(タウ)」に該当。
- 南極=あるいは。球表面上における「観測始点」の対蹠点。極座標系(polar coordinates system)における「距離-1、角度180度あるいはπRadianあるいは1/2τ(タウ)」に該当。
正方形(Square)の世界ではさらに(単位球面上に想定される)単位円(Unit Circle)上に以下の4点が追加で想定される。
- 0度/360度=あるいは0Radian/2πRadianあるいは0τ=1τ(タウ)
- 90度=あるいはπ/2Radianあるいは1/4τ(タウ)
- 180度=あるいはπRadianあるいは1/2τ(タウ)
- 270度=あるいは3/2Radianあるいは3/2τ(タウ)、さらには-90度あるいは-π/2Radianあるいは-1/4τ(タウ)

まぁ「継ぎ接ぎ」の数だけ「ジンバルロック点」が生じてしまうのは仕方ない?

まさしく「オイラーの剛腕」あるいは「フランケンシュタイン博士の怪物の誕生」といった風情。継ぎ接ぎだらけの不恰好で醜い悪足掻きの産物。

最近こういう話題になると脳内にこの曲が流れます。
何もない僕達に、何故夢を見させたか。
終わりある人生に、何故希望を持たせたか。
何故この手をすり抜けるものばかり与えたか。
それでもしがみつく僕らは醜いかい?
それとも綺麗かい?
答えてよ(誰が?)
まさしくTV番組だったら最後に流れるエンディング・テーマみたいな感じで…