【正多辺形方程式情報倉庫】「オイラーの公式」の「正多辺形方程式（Regular Polisides equattion）」への拡張

三角関数や自然対数を使って円が描ける様になると、ちょっとした応用でどんな正多辺形（Regular Polisides）も描ける様になります。

f:id:ochimusha01:20190818003553g:plain

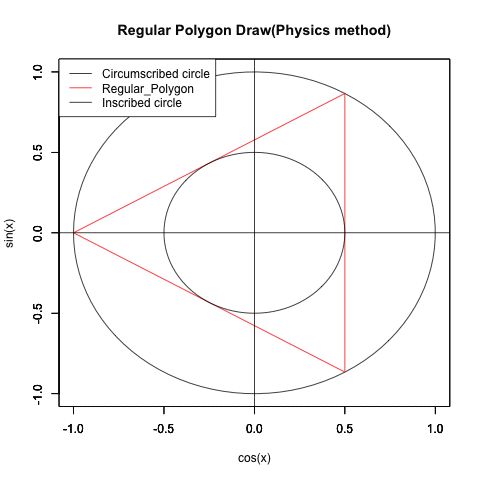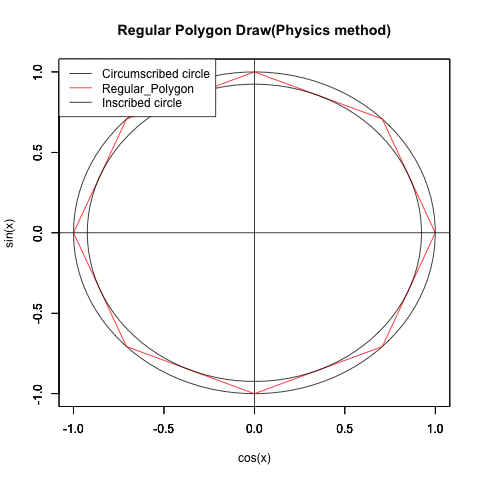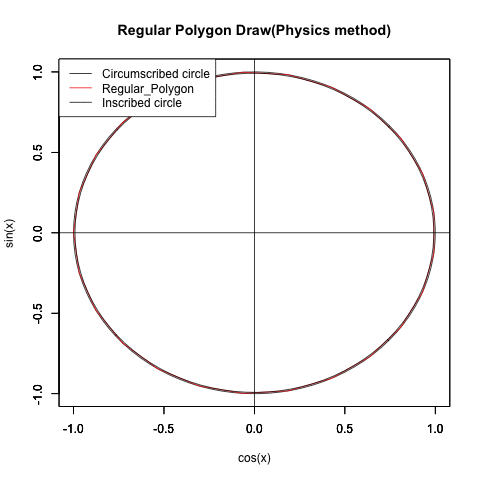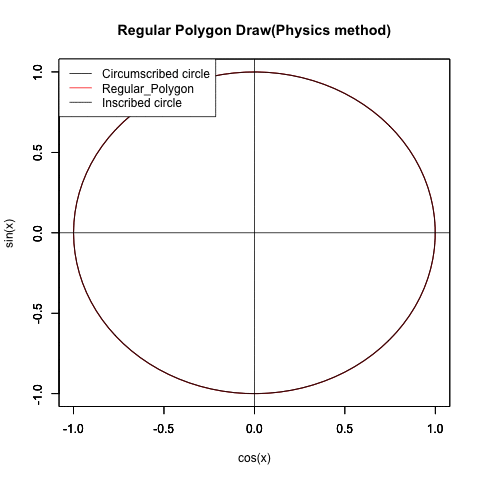
ところで意外にも正多辺形（Regular Polisides）の「辺数(NoC=Number of Sides)」は連続する実数としても扱える様なのです。

正多角形の定義をどうするか、ということもある。定義の仕方によっては、正2.5角形も描けたりする。

「正多角形をつくろう」(ビデオ2:26:00あたりから)https://t.co/LHCLnu7eNJ https://t.co/BiSdKqW9L7
— 野中文雄 (@FumioNonaka) December 6, 2018

この考え方を援用すれば「円を描く方程式（Circle equation）」を代表する一つ「オイラーの公式（Euler's formula）e^θi=cos(θ)+sin(θ)i」の一般形たる「正多辺形方程式（Regular Polisides equattion）Cos(θ)+Cos(θ-π/NoC)i)」へと拡張する事が可能となります。

正多辺形方程式（Regular Polisides equattion）Cos(θ)+Cos(θ-π/NoC)i)は、オイラーの公式cos(θ)+sin(θ)iが現れる辺数(NoC=Number of Sides)の判別式としても使える。例えば角度θ=0~πの周期を与えた場合は1がその答えとなる。

統計言語Rによるプログラミング例

WEA<-function(x_min,x_max){
c0<-seq(0,2*pi,60)
f0<-function(x){cos(c0)+cos(c0-pi/x)}
plot(f0,xlim=c(x_min,x_max),main="When Euler's formula appear?",xlab="NoC(Number of Corners)",ylab="cos(θ)+cos(θ-π/Noc)")
abline(h=1,col=rgb(1,0,0))
}

１角形（Henagon）以上の世界ではこの条件を満たすのは2角形（Digon）のみ。以降はこの判別式の上限たる2に向けてゆっくり収束していく。
統計言語Rによるプログラミング例

WEA(1,8)

１角形（Henagon）未満の世界ではこの条件を満たす図形が出現周期を短縮しつつ、この判別式の下限たる0に向けて無限に現れ続ける。
統計言語Rによるプログラミング例

WEA(1,0)
具体的にこの条件を満たすのは辺数(NoS)=2/(2N+1)の条件を満たすケース。すなわち2辺形、2/3辺形、2/5辺形、2/7辺形…と出現周期を短縮しつつ0に向けて収束していく訳である。

一体何が起こっているか複素平面（Complex plane）上でも確認（Confirm）してみましょう。正多辺形方程式（Regular Polisides equattion）Cos(θ)+Cos(θ-π/NoC)iの値は、角数(NoC)=1、辺数（NoS=Number of Side）=1（辺長（LoS=length of Side）2πあるいは1τ）の1角形（Henagon）の時にCos(θ)-Cos(θ)i,角数(NoC)、辺数（NoS）ともに無限大（辺長(LoS)は無限小）の円そのもの(Circle itself)の理論値たるCos(θ)+Cos(θ)iに無限収束を続けます。

1角形（Henagon）の統計言語Rによるプログラミング例。

c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)*-1
plot(cx,cy,type="o",main="Cos(θ) orthogonal -Cos(θ) ",xlab="cos(θ)",ylab="-cos(θ)")
#凡例
legend("bottomleft", legend=c("cos(θ) orthogonal -cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))

f:id:ochimusha01:20191024163532p:plain

1角形（Henagon）の統計言語Rによるプログラミング例。

c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-sin(c0)
plot(cx,cy,asp=1,type="o",main="Cos(θ) orthogonal Sin(θ) ",xlab="cos(θ)",ylab="sin(θ)")
#凡例
legend("bottomleft", legend=c("cos(θ) orthogonal sin(θ) "), lty=c(1), col=c(rgb(0,0,0)))

円そのもの(Circle itself)の統計言語Rによるプログラミング例。

c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0)
plot(cx,cy,type="o",main="Cos(θ) orthogonal Cos(θ) ",xlab="cos(θ)",ylab="cos(θ)")
#凡例
legend("bottomright", legend=c("cos(θ) orthogonal cos(θ) "), lty=c(1), col=c(rgb(0,0,0)))

f:id:ochimusha01:20191024163830p:plain

そしてその間、2角形（Digon）の状態においてのみオイラーの公式（Euler's formula）e^θi=cos(θ)+sin(θ)iが成立するのです。

f:id:ochimusha01:20191024163746p:plain

もう大体、どういう展開となるかは見切れましたね。それでは実践…
統計言語Rによるプログラミング例

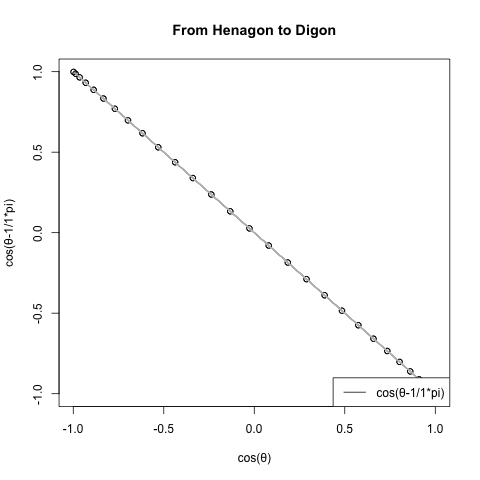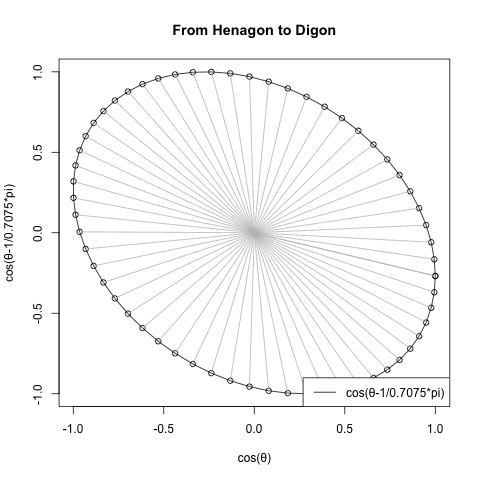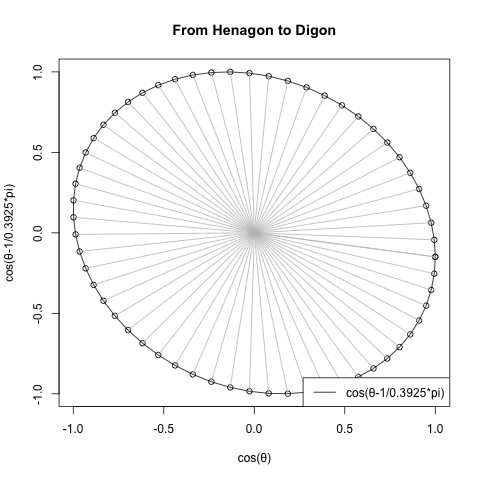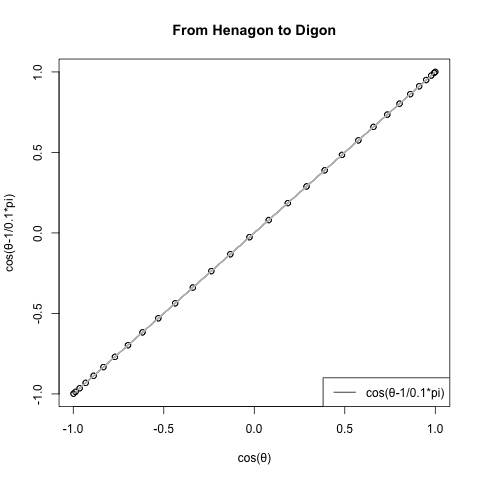
#FHtD=1角形から2角形へ（From Henagon to Digon）
#Noc=角数(Number of corners)
FHtD<-function(NoC){
c0<-seq(0,2*pi,length=60)
cx<-cos(c0)
cy<-cos(c0-1/NoC*pi)
text01<-paste0("cos(θ-1/",round(NoC,4),"*pi)")
plot(cx,cy,type="o",main="From Henagon to Digon",xlab="cos(θ)",ylab=text01)

#中心からの補助線
cx0<-rep(0, length=length(cx))
cy0<-rep(0, length=length(cy))
segments(cx0, cy0, cx, cy,col=c(200,200,200))

#凡例
legend("bottomright", legend=text01,lty=c(1), col=c(rgb(0,0,0)))
}

統計言語Rによるプログラミング例（1角形〜円そのものへ。あまりに収束が遅いので途中で加速している）

#アニメーション
library("animation")
Time_Code=c(seq(1,6, length=50),seq(6,64,length=20))
saveGIF({
for (i in Time_Code){
FHtD(i)
}
}, interval = 0.1, movie.name = "FHtD01.gif")

f:id:ochimusha01:20191019011127g:plain