対数関数(Logarithm Function)x=±a(1/a)^yあるいはy=±log(x,base=a(1/a))ではなく、指数関数(Exponential Function)y=±a(1/a)^xだけが文字通り「指数級的(Exponential)展開」による「 有意味な増大(SI=Significant increase)」や「有意味な減少(SR=Significant reduction)」と「無視可能な状態(IS=Ignorable State)」の往復を提示するのです。増大率上限e^1=e(2.718282)、標準失敗率e^-1=1/e(0.3678794)、標準成功率1-e^-1(0.6321206)の世界?
- y=a^x…「無視可能な状態(IS=Ignorable State)」から「 有意味な増大(SI=Significant increase)」へ。転回点は座標[0,1]あるいは複素座標Cos(π/2=0)+Sin(π/2=1)i=0+1iとなる。
- y=(1/a)^x…「有意味な減少(SR=Significant reduction)」から「無視可能な状態(IS=Ignorable State)」へ。転回点は同様に座標[0,1]あるいは複素座標Cos(π/2=0)+Sin(π/2=1)i=0+1iとなる。
- y=-a^x…「無視可能な状態(IS=Ignorable State)」から「有意味な減少(SR=Significant reduction)」へ。転回点は座標[0,-1]あるいは複素座標Cos(-π/2=3/4π=0)+Sin(-π/2=3/4π=-1)i=0+-1iとなる。
- y=-(1/a)^x…「 有意味な増大(SI=Significant increase)」から「無視可能な状態(IS=Ignorable State)」へ。転回点は同様に座標[0,-1]あるいは複素座標Cos(-π/2=3/4π=0)+Sin(-π/2=3/4π=-1)i=0+-1iとなる。
- 精神物理学によれば、そもそも心理的感覚Sと刺激の物理的強度Iの間にS=Klog(I)の非線形関係がある。Kは定数でウェーバー比と呼ばれ、たとえば音の強さについては 11分の1,圧覚では7分の1と定められている。


- その一方で実際の自然界に対する観測においてはロジスティック方程式を意識せねばならない局面も存在するので注意が必要。
まず基本から。指数(-n,-1,0,1,n)に対して(1/base^x,1/base^x,base/base,base,base^x)となるを返す指数関数y=底(root)^xや、逆に指数(-n,-1,0,1,n)を返す対数関数x=底(root)^yもしくはlog(x,base=底(root))は、以下の区間から構成されています。
#指数関数と対数関数の結果の対応
section01<-c("Past","Current","Current","Current","future")
exponential_result01<-c("root^-x","root^-1=1/root","root^0=root/root=1","root^1=root","root^x")
logarithm_result01<-c("log(1/root^x,base=root)=-x","log(1/root,base=root)=-1","log(1,base=root)=0","log(root,base=root)=1","log(root^x,base=root)=x")
Exponential_and_Logarithm01<-data.frame(Section=section01,Exponential_result=exponential_result01,Logarithm_result=logarithm_result01)
library(xtable)
print(xtable(Exponential_and_Logarithm01), type = "html")
| Section | Exponential_result | Logarithm_result | |
|---|---|---|---|
| 1 | Past | root^-x | log(1/root^x,base=root)=-x |
| 2 | Current | root^-1=1/root | log(1/root,base=root)=-1 |
| 3 | Current | root^0=root/root=1 | log(1,base=root)=0 |
| 4 | Current | root^1=root | log(root,base=root)=1 |
| 5 | future | root^x | log(root^x,base=root)=x |
*概ねネイピア数eを底(root)とする指数関数e^xと指数関数log(x,base=e)を中心に考える。この時、底(root)のズレは指数関数y=e^(log(底(root))*x).対数関数の場合はx=e^(log(底(root))*y)すなわちy=log(x)/log(底(root))と対応される。
#統計言語Rによる図示例。
f0<-function(x){exp(x)}
f1<-function(x){log(x)}
plot(f0,xlim=c(-8,8),ylim=c(-1,8),type="l",col=rgb(1,0,0), main="Exponential and logarithmic functions to base Napier number", xlab="x", ylab="y")
par(new=T)#上書き指定
plot(f1,xlim=c(-8,8),ylim=c(-1,8),col=rgb(0,0,1),main="", xlab="", ylab="")
legend("topleft", legend=c("y=e^x", "y=log(x)"), lty = c(1,1),col=c(rgb(1,0,0),rgb(0,0,1)))

過去(Past)…指数関数の指数でいう-1未満の区間。
無視可能な状態(Ignorable State = 1/(root^x))の実例(IR)
#指数関数2^xあるいは対数関数log(x,base=2)の場合
target_numbers<-c("0.5=1/2","0.25=1/4","0.125=1/8","0.0625=1/16")
exponential_result<-c("2^-1=0.5","2^-2=0.25","2^-3=0.125","2^-4=0.0625")
logarithm_result<-c("log2(0.5)=-1","log2(0.25)=-2","log2(0.125)=-3","log2(0.0625)=-4")
Exponential_and_Logarithm<-data.frame(Target_numbers=target_numbers,Exponential_result=exponential_result,Logarithm_result=logarithm_result)
library(xtable)
print(xtable(Exponential_and_Logarithm), type = "html")
| Target_numbers | Exponential_result | Logarithm_result | |
|---|---|---|---|
| 1 | 0.5=1/2 | 2^-1=0.5 | log2(0.5)=-1 |
| 2 | 0.25=1/4 | 2^-2=0.25 | log2(0.25)=-2 |
| 3 | 0.125=1/8 | 2^-3=0.125 | log2(0.125)=-3 |
| 4 | 0.0625=1/16 | 2^-4=0.0625 | log2(0.0625)=-4 |
未来(Future)…指数関数の指数でいう1以上の区間。
「 有意味な増大(Significant increase)」の実例(IS->SI)
#指数関数と対数関数の結果の対応
target_numbers<-c("4","8","16")
exponential_result<-c("2^2=4","2^3=8","2^4=16")
logarithm_result<-c("log2(4)=2","log2(8)=3","log2(16)=4")
Exponential_and_Logarithm<-data.frame(Target_numbers=target_numbers,Exponential_result=exponential_result,Logarithm_result=logarithm_result)
library(xtable)
print(xtable(Exponential_and_Logarithm), type = "html")
| Target_numbers | Exponential_result | Logarithm_result | |
|---|---|---|---|
| 1 | 4 | 2^2=4 | log2(4)=2 |
| 2 | 8 | 2^3=8 | log2(8)=3 |
| 3 | 16 | 2^4=16 | log2(16)=4 |
現在(Current)…指数関数の指数でいう-1から+1にかけての区間。オイラーの等式e^iπ=-1やオイラーの公式e^iΘ=cos(Θ)+sin(Θi)などが切り抜いて単位円(半径1の円弧)に対応させる箇所。

①指数関数y=底(base)^x、対数関数x=底(root)^yもしくはlog(x,base=底(root))。底(root)の値はroot。
統計言語Rによる実際の計算例
#指数関数2^x
2^-1
[1] 0.5
2^0
[1] 1
2^1
[1] 2
#対数関数log(x,base=2)
log(1/2,base=2)
[1] -1
log(1,base=2)
[1] 0
log(2,base=2)
[1] 1
②底を逆転させた指数関数y=1/(底(base))^x、対数関数x=1/(底(root))^yもしくは-log(x,base=1/底(root))。指数との対応が逆転する。底(root)の値は1/root(root^-1)。
統計言語Rによる実際の計算例
#指数関数(1/2)^x
(1/2)^-1
[1] 2
(1/2)^0
[1] 1
(1/2)^1
[1] 0.5#対数関数log(x,base=1/2)
log(2,base=1/2)
[1] -1
log(1,base=1/2)
[1] 0
log(1/2,base=1/2)
[1] 1
③ここでいう①の式の符号を逆転させた指数関数y=-底(base)^x、対数関数x=-底(root)^yもしくはy=-log(x,base=底(root))。底(root)の値は-root。
統計言語Rによる実際の計算例
#指数関数-2^x
-2^-1
[1] -0.5
-2^0
[1] -1
-2^1
[1] -2
#対数関数-log(x,base=2)
log(1/2,base=2)
[1] -1
log(1,base=2)
[1] 0
log(2,base=2)
[1] 1
④ここでいう②の式の符号を逆転させた指数関数y=-1/(底(base))^x、対数関数x=-1/(底(root))^yもしくは-log(x,base=1/底(root))。底(root)の値は-1/root(-root^-1)。
統計言語Rによる実際の計算例
#指数関数(1/2)^x
-(1/2)^-1
[1] -2
-(1/2)^0
[1] -1
- (1/2)^1
[1] -0.5
#対数関数log(x,base=1/2)
-log(2,base=1/2)
[1] 1
-log(1,base=1/2)
[1] 0
-log(1/2,base=1/2)
[1] -1
指数関数y=底(base)^xから指数関数y=1/(底(base))^xへの底(root)移動。指数0時点で傾きが消失しy=1となる。
#指数関数root^x
if01<-f0<-function(n){
f0<-function(x){2^x}
plot(f0,xlim=c(-5,5),ylim=c(0,5),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="2^x ~ (1/2)^x")
par(new=T)#上書き指定
f1<-function(x){1/2^x}
plot(f1,xlim=c(-5,5),ylim=c(0,5),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){n^x}
plot(f2,xlim=c(-5,5),ylim=c(0,5),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")abline(h=1)
abline(v=0)tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals <- f2(tc) #それぞれの縦軸の値polygon(c(-6,tc,6), #x
c(1,tcvals,1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色legend("topleft", legend=c("y=2^x","y=1/2^x","x=0,y=1"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if01(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

指数関数y=-底(base)^xから指数関数y=-1/(底(base))^xへの底(root)移動。指数0時点で傾きが消失しy=-1となる。
#指数関数-1*(root^x) ~ -1**1 #塗りつぶす色
legend("bottomright", legend=c("y=-(2^x)","y=-(1/2^x)","x=0,y=-1"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if01(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

対数関数x=底(root)^yもしくはlog(x,base=底(root))から対数関数x=1/(底(root))^yもしくはlog(x,base=1/底(root))への底(root)移動。指数0時点で傾きが消失しx=1となる。
#対数関数 log(x,base=root)
if02<-f0<-function(n){
f0<-function(x){log(x,base=2)}
plot(f0,xlim=c(0,5),ylim=c(-5,5),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="log(x,base=2~1/2)")
par(new=T)#上書き指定
f1<-function(x){log(x,base=1/2)}
plot(f1,xlim=c(0,5),ylim=c(-5,5),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){log(x,base=n)}
plot(f2,xlim=c(0,5),ylim=c(-5,5),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
abline(h=0)
abline(v=1)f3<-function(x){n^x}
tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals <- f3(tc) #それぞれの縦軸の値polygon(c(1,tcvals,1), #x
c(-6,tc,6), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
legend("topleft", legend=c("y=log(x,base=2)","y=log(x,base=1/2)","x=1,y=0"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if02(i)
}
}, interval = 0.1, movie.name = "TEST02.gif")

対数関数x=-底(root)^yもしくは-log(x,base=底(root))から対数関数x=-1/(底(root))^yもしくは-log(x,base=1/底(root))への底(root)移動。指数0時点で傾きが消失しx=1となる。
#対数関数 log(x,base=root)にマイナス符号をかけて反転
if02<-f0<-function(n){
tc <- seq(-6, 6, length=60) #-6から6までを60等分
f0<-function(x){-1*(2^x)}
tcvals0 <- f0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,xlim=c(-5,0),ylim=c(-5,5),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="log(x,base=2~1/2)")
par(new=T)#上書き指定
f1<-function(x){-1**2 #塗りつぶす色
legend("topleft", legend=c("y=-log(x,base=2)","y=-log(x,base=1/2)","x=-1,y=0"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0),rgb(0,0,0)))
}
library("animation")
Time_Code=c(2.0,1.8,1.6,1.4,1.2,1.0,0.9,0.8,0.7,0.6,0.5,0.6,0.7,0.8,0.9,1.0,1.2,1.4,1.6,1.8)
saveGIF({
for (i in Time_Code){
if02(i)
}
}, interval = 0.1, movie.name = "TEST02.gif")

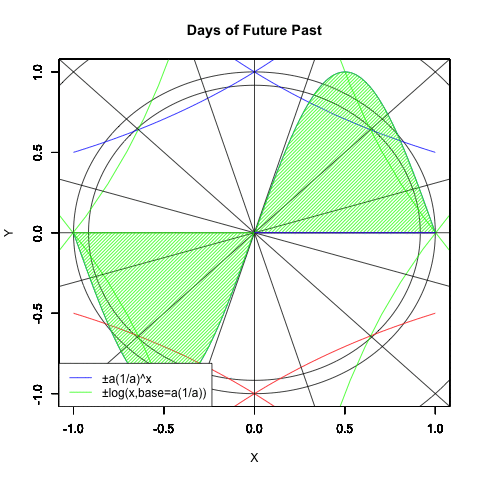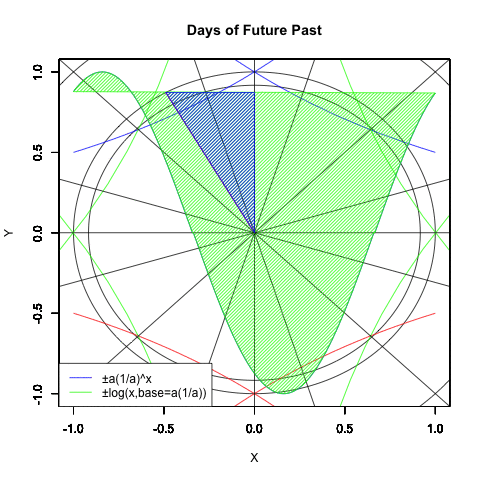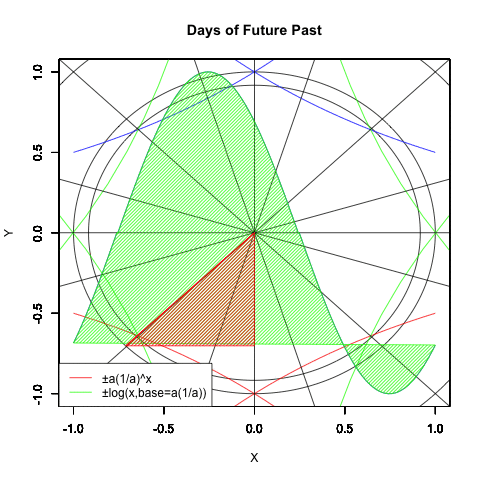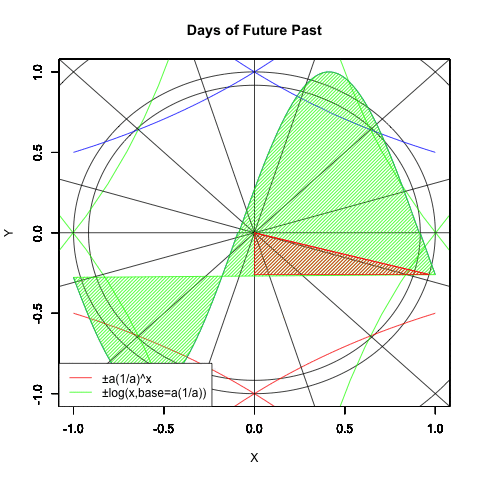
全部合わせると以下の様になる。各曲線は単位円(半径1の円弧)上における0度(0ラジアン),90度(1/2πラジアン),180度(πラジアン)270度(3/2πラジアン)だけでなく、半径root^(-1/8)の円弧上の45度(1/4πラジアン),135度(3/4πラジアン),225度(5/4πラジアン),315度(7/4πラジアン)、半径root^(1/2)の円弧上の18度(π/10ラジアン),72度(1/2π-π/10ラジアン),108度(1/2π+π/10ラジアン),162度(π-π/10ラジアン),198度(π+π/10ラジアン),252度(3/4π-π/10ラジアン),288度(3/4π+π/10ラジアン),378度(2π-π/10ラジアン)で交差する。
#各指数関数・対数関数の交差点
Graph_scale_x<-c(-2,2)
Graph_scale_y<-c(-2,2)
theta <- seq(pi, -pi, length=360)
plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Days of Future Past", xlab="X", ylab="Y")par(new=T)#上書き指定
plot(cos(theta)* 2^(-1/8), sin(theta)* 2^(-1/8), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定par(new=T)#上書き指定
plot(cos(theta)*2/sqrt(2), sin(theta)*2/sqrt(2), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定
#指数関数
e0<-function(x){2^x}
plot(e0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e1<-function(x){1/2^x}
plot(e1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e2<-function(x){-1*(2^x)}
plot(e2,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e3<-function(x){-1*(1/2)^x}
plot(e3,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定#対数関数
tc <- seq(-6, 6, length=60) #-6から6までを60等分
l0<-function(x){2^x}
tcvals0 <- l0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定l1<-function(x){(1/2)^x}
tcvals1 <- l1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l2<-function(x){-1*(2^x)}
tcvals2 <- l2(tc) #それぞれの縦軸の値
plot(tcvals2,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l3<-function(x){-1**3
segments(-8,8,8,-8,col=rgb(0,0,0))
#18度(π/10)/72度の補助線
segments(-8,-(sin(pi/10))*8,8,(sin(pi/10))*8,col=rgb(0,0,0))
segments(-8,(sin(pi/10))*8,8,-1*(sin(pi/10))*8,col=rgb(0,0,0))
segments(-(sin(pi/10))*8,-8,(sin(pi/10))*8,8,col=rgb(0,0,0))
segments*4*8,-8,-1*(sin(pi/10))*8,8,col=rgb(0,0,0))
legend("bottomleft", legend=c("±a(1/a)^x","±log(x,base=a(1/a)))"),lty=c(1,1),col=c(rgb(0,0,1),rgb(0,1,0)))

統計言語Rによる実際の計算例
#同心円2^(-1/8)2^(-1/8))
[1] 0.917004#同心円2^(1/2)
2/sqrt(2)
[1] 1.414214
2^0.5
[1] 1.414214
単位円(半径1の円弧)上における0度(0ラジアン),90度(1/2πラジアン),180度(πラジアン)270度(3/2πラジアン)の交差
#指数関数と対数関数の結果の対応
degrees_and_radians<-c("0Degrees(0Radians)","90Degrees(1/2πRadians)","180Degrees(πRadians)","270Degrees(3/2πRadians)")
fanctions01<-c("log(x,base=a)(IS) & log(x,base=1/a)(IS)","root^x(IS->SI) & 1/root^x(SR->IS)","-log(x,base=a)(IS) & -log(x,base=1/a)(IS)","-root^x(IS->SR) & -1/root^x(SI->IS)")
DRF01<-data.frame(Degrees_and_Radians=degrees_and_radians,Cross_Fanctions=fanctions01)
library(xtable)
print(xtable(DRF01), type = "html")
| Degrees_and_Radians | Cross_Fanctions | |
|---|---|---|
| 1 | 0Degrees(0Radians) | log(x,base=a)(IS) & log(x,base=1/a)(IS) |
| 2 | 90Degrees(1/2πRadians) | root^x(IS->SI) & 1/root^x(SR->IS) |
| 3 | 180Degrees(πRadians) | -log(x,base=a)(IS) & -log(x,base=1/a)(IS) |
| 4 | 270Degrees(3/2πRadians) | -root^x(IS->SR) & -1/root^x(SI->IS) |
半径root^(-1/8)の円弧上の45度(1/4πラジアン),135度(3/4πラジアン),225度(5/4πラジアン),315度(7/4πラジアン)の交差
#指数関数と対数関数の結果の対応
degrees_and_radians02<-c("45Degrees(1/4πRadians)","135Degrees(3/4πRadians)","225Degrees(5/4πRadians)","315Degrees(7/4πRadians)")
fanctions02<-c("1/root^x(SR->IS) & log(x,base=a)(IS)","root^x(IS->SI) & -log(x,base=a)(IS) ","-root^x(IS->SR) & -log(x,base=1/a)(IS) ","-1/root^x(SI->IS) & log(x,base=a)(IS)")
DRF02<-data.frame(Degrees_and_Radians=degrees_and_radians02,Cross_Fanctions=fanctions02)
library(xtable)
print(xtable(DRF02), type = "html")
| Degrees_and_Radians | Cross_Fanctions | |
|---|---|---|
| 1 | 45Degrees(1/4πRadians) | 1/root^x(SR->IS) & log(x,base=1/a)(IS) |
| 2 | 135Degrees(3/4πRadians) | root^x(IS->SI) & -log(x,base=a)(IS) |
| 3 | 225Degrees(5/4πRadians) | -root^x(IS->SR) & -log(x,base=1/a)(IS) |
| 4 | 315Degrees(7/4πRadians) | -1/root^x(SI->IS) & log(x,base=a)(IS) |
半径root^(1/2)の円弧上の18度(π/10ラジアン),72度(1/2π-π/10ラジアン),108度(1/2π+π/10ラジアン),162度(π-π/10ラジアン),198度(π+π/10ラジアン),252度(3/4π-π/10ラジアン),288度(3/4π+π/10ラジアン),378度(2π-π/10ラジアン)の交差
#指数関数と対数関数の結果の対応
degrees_and_radians03<-c("18Degrees(π/10Radians)","72Degrees(1/2π-π/10Radians)","108Degrees(1/2π-π/10Radians)","162Degrees(π-π/10Radians)","198Degrees(π+π/10Radians)","252Degrees(3/4π-π/10Radians)","288Degrees(3/4π+π/10Radians)","378Degrees(2π-π/10Radians)")
fanctions03<-c("1/root^x(SR->IS) & log(x,base=a)(IS)","root^x(IS->SI) & log(x,base=1/a)(IS)","1/root^x(SR->IS) & -log(x,base=1/a)(IS)","root^x(IS->SI) & -log(x,base=a)(IS)","-root^x(IS->SR) & -log(x,base=1/a)(IS)","-1/root^x(SI->IS) & -log(x,base=a)(IS)","-root^x(IS->SR) & log(x,base=a)(IS)","-1/root^x(SI->IS) & log(x,base=1/a)(IS)")
DRF03<-data.frame(Degrees_and_Radians=degrees_and_radians03,Cross_Fanctions=fanctions03)
library(xtable)
print(xtable(DRF03), type = "html")
| Degrees_and_Radians | Cross_Fanctions | |
|---|---|---|
| 1 | 18Degrees(π/10Radians) | 1/root^x(SR->IS) & log(x,base=a)(IS) |
| 2 | 72Degrees(1/2π-π/10Radians) | root^x(IS->SI) & log(x,base=1/a)(IS) |
| 3 | 108Degrees(1/2π-π/10Radians) | 1/root^x(SR->IS) & -log(x,base=1/a)(IS) |
| 4 | 162Degrees(π-π/10Radians) | root^x(IS->SI) & -log(x,base=a)(IS) |
| 5 | 198Degrees(π+π/10Radians) | -root^x(IS->SR) & -log(x,base=1/a)(IS) |
| 6 | 252Degrees(3/4π-π/10Radians) | -1/root^x(SI->IS) & -log(x,base=a)(IS) |
| 7 | 288Degrees(3/4π+π/10Radians) | -root^x(IS->SR) & log(x,base=a)(IS) |
| 8 | 378Degrees(2π-π/10Radians) | -1/root^x(SI->IS) & log(x,base=1/a)(IS) |
こうした偏りは、間違いなくネイピア数eを底(root)をy軸に採った指数関数e^xやlog(x)関数の振る舞い、およびそれに立脚するオイラーの等式e^πi=-1と無関係ではなさそうです。
その基準円(半径1の円弧)上の振る舞いについては、三角関数に分類されているサイン関数sin(Θ)を彷彿とさせる側面も。
統計言語Rによる作表例
target_names<-c("0 radian & 0 degree","π/2 radian & 90 degree","π radian & 180 degree","3/2π& 270 degree","2π & 360 degree")
target_values<-c("0","1","0","-1","0")
Circular_function<-data.frame(Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Circular_function), type = "html")
| Target_names | Target_values | |
|---|---|---|
| 1 | 0 radian & 0 degree | 0 |
| 2 | π/2 radian & 90 degree | 1 |
| 3 | π radian & 180 degree | 0 |
| 4 | 3/2π& 270 degree | -1 |
| 5 | 2π & 360 degree | 0 |
統計言語Rでの実証例
#複素平面(球面)
Complex_plane<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_sin<-sin(theta01)
#方向の正負
ifelse*5#円弧の描写
plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Days of Future Past", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(cos(theta)* 2^(-1/8), sin(theta)* 2^(-1/8), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定
plot(cos(theta)*2/sqrt(2), sin(theta)*2/sqrt(2), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="", xlab="", ylab="")
par(new=T)#上書き指定
#指数関数
e0<-function(x){2^x}
plot(e0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e1<-function(x){1/2^x}
plot(e1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,1), main="",xlab="",ylab="")
par(new=T)#上書き指定
e2<-function(x){-1*(2^x)}
plot(e2,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
e3<-function(x){-1*(1/2)^x}
plot(e3,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
par(new=T)#上書き指定#対数関数
tc <- seq(-6, 6, length=60) #-6から6までを60等分
l0<-function(x){2^x}
tcvals0 <- l0(tc) #それぞれの縦軸の値
plot(tcvals0,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定l1<-function(x){(1/2)^x}
tcvals1 <- l1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l2<-function(x){-1*(2^x)}
tcvals2 <- l2(tc) #それぞれの縦軸の値
plot(tcvals2,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
l3<-function(x){-1**6
segments(-8,8,8,-8,col=rgb(0,0,0))
#18度(π/10)/72度の補助線
segments(-8,-(sin(pi/10))*8,8,(sin(pi/10))*8,col=rgb(0,0,0))
segments(-8,(sin(pi/10))*8,8,-1*(sin(pi/10))*8,col=rgb(0,0,0))
segments(-(sin(pi/10))*8,-8,(sin(pi/10))*8,8,col=rgb(0,0,0))
segments*7*8,-8,-1*(sin(pi/10))*8,8,col=rgb(0,0,0))
#サイン波(ポリゴン)
polygon(theta00, #x
theta_sin, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色#インジケーター
segments(cos(dr[x]),sin(dr[x]),0,0,col=segC)
polygon(c(cos(dr[x]),0,0), #x
c(sin(dr[x]),sin(dr[x]),0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
#凡例
col=segC) #塗りつぶす色legend("bottomleft",legend=c("±a(1/a)^x","±log(x,base=a(1/a))"),lty=c(1,1),col=c(segC,rgb(0,1,0)))
}
#アニメーションさせてみる。library("animation")
#Time_Code=c(1,90,180,270)
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

とりあえず、思いついてしまったのでメモがてら…
*1:1/root)^x)にマイナス符号をかけて反転
if01<-f0<-function(n){
f0<-function(x){-1*(2^x)}
plot(f0,xlim=c(-5,5),ylim=c(-5,0),type="l",col=rgb(0,0,1), main="Days of Future Past",xlab="x",ylab="2^x ~ (1/2)^x")
par(new=T)#上書き指定
f1<-function(x){-1*(1/2)^x}
plot(f1,xlim=c(-5,5),ylim=c(-5,0),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){-1*(n^x)}
plot(f2,xlim=c(-5,5),ylim=c(-5,0),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
abline(h=-1)
abline(v=0)
tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals <- f2(tc) #それぞれの縦軸の値
polygon(c(-6,tc,6), #x
c(-1,tcvals,-1), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0
*2:1/2)^x)}
tcvals1 <- f1(tc) #それぞれの縦軸の値
plot(tcvals1,tc,xlim=c(-5,0),ylim=c(-5,5),type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
f2<-function(x){-1*log(x,base=n)}
plot(f2,xlim=c(-5,0),ylim=c(-5,5),type="l",col=rgb(1,0,0), main="",xlab="",ylab="")
abline(h=0)
abline(v=-1)
f3<-function(x){-1*(n^x)}
tc <- seq(-6, 6, length=60) #-6から6までを60等分
tcvals3 <- f3(tc) #それぞれの縦軸の値
polygon(c(-1,tcvals3,-1), #x
c(-6,tc,6), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0
*3:1/2)^x)}
tcvals3 <- l3(tc) #それぞれの縦軸の値
plot(tcvals3,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
#90度(π/2)の補助線
abline(h=0)
abline(v=0)
#45度(π/4)の補助線
segments(-8,-8,8,8,col=rgb(0,0,0
*4:sin(pi/10
*5:x>180),segC<-rgb(1,0,0),segC<-rgb(0,0,1
*6:1/2)^x)}
tcvals3 <- l3(tc) #それぞれの縦軸の値
plot(tcvals3,tc,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,1,0), main="",xlab="",ylab="")
par(new=T)#上書き指定
#サイン波
plot(theta00,theta_sin,xlim=Graph_scale_x, Graph_scale_y, type="l",col=rgb(0,0,1),,main="",xlab="", ylab="")
#90度(π/2)の補助線
abline(h=0)
abline(v=0)
#45度(π/4)の補助線
segments(-8,-8,8,8,col=rgb(0,0,0
*7:sin(pi/10