
オイラーの等式e^iπ=(1-iπ/N)^N=(1+iπ/N)^N=-1は(角度の特定はともかく)辺長の合計の極限値が「2π(極限値)」で対角線の全長が「2」の(平面上でのイメージ化は不可能だが、球面上においては容易にイメージ化可能な)正2角形を現出させます。
正二角形 pic.twitter.com/gH4xT4W5jT
— ぷしゅたろん@海未凛 (@ainshutain3110) May 18, 2014

もしそれが「半径1の円弧」だったら、数理モデルとしてどれほど都合が良い事でしょう。先験的直感はさらに「どうしてそれ以外のケースなど考えられるというのか、まさにそうに違いない(反語表現)」と囁いてきます。これが、いわゆる「解析接続(analytic continuation,/analytic prolongation)」の発想の大源流?
いずれにせよ、ここまで辿り着いたら観測原点「0」と対象「1」とを結ぶ距離1の線分の旋回範囲に、それを半径とする円周/円や球面/球のイメージが形成されるのは自然の成り行きとなります。おそらく微積分の概念の起源もまた、この辺りまで遡り得るのです。
統計言語Rによる検証例
#半径rの円の面積(pi*r^2)をrで微分(Differential)すると円周の長さ(2*pi*r)となる。
D01<-expression(pi*r^2)
D(D01,"r")
pi * (2 * r)#半径rの球の体積(4/3*pi*r^3)をrで微分(Differential)すると球の表面積(4*pi*r^2)となる。
D02<-expression(4/3*pi*r^3)
D(D02,"r")
4/3 * pi * (3 * r^2)
汎用計算機代数ソフトウェア"Yacas"による検証例
GNU General Public License にしたがった利用と配布が認められている汎用計算機代数アプリケーションのフリーソフトウェア。名前は Yet Another Computer Algebra System から来ている。
計算機代数の演算を行うシステムであるため、数式の記号操作ができる。また記号計算および任意精度の数値計算を行うための独自のプログラミング言語処理系を備えている。多くの数式処理操作を実装したスクリプトのライブラリを持っており、新たに実装したアルゴリズムの追加が容易に行えるようになっている。スクリプト言語および実装されている機能とアルゴリズムについての文書が多数用意されている。
この数理モデルにおける半径rの球の体積と球の表面積の関係は「同心球の積層」 、円の面積と円周の長さの関係は「同心円の積層」というイメージ。
- 小学校の時、円の面積pi*r^2は「距離1の線分の回転」によって細かく刻まれた三角形の集合▲▲▲▲▲を▲▼▲▼▲▼▲▼と並べ直して平行四辺形を求める式を適用し、底辺=π*rと高さrの掛け算で求めると教えられた。
- その応用で、球の表面積4*pi*r^2は同様に刻まれた幅rΔΘで円周2*pi*r*cos(Θ)の同心円をπ/2から-π/2にかけて積層するイメージ。
統計言語Rによる検証例#-pi/2からpi/2にかけてのcos(ΔΘ)の積層結果(数値積分)
integrate(cos,-pi/2,pi/2)
2 with absolute error < 2.2e-14
「オイラーの原始量(Euler's primitive sweep)」は、それこそ人間未満の生物に起源を有する様な粗雑な思考様式なので「とりあえず長さ1とみなした棒をグルグル振り回すと、その先端が円や球を描く」くらいの考え方しか出来ません。
統計言語Rによる検証例(線分から円の面積へ)
#複素平面(球面)
Complex_plane<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_sin<-sin(theta01)
#方向の正負(左右とも緑)
segC<-rgb(0,1,0)
theta02<-dr[1:x]
theta02_cos<-cos(theta02)
theta02_sin<-sin(theta02)
#円弧の描写plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Circle area", xlab="X", ylab="Y")
#インジケーター
segments(cos(dr[x]),sin(dr[x]),0,0,col=segC)
polygon(c(theta02_cos,0), #x
c(theta02_sin,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=segC) #塗りつぶす色}
#アニメーションさせてみる。library("animation")
#Time_Code=c(1,90,180,270)
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

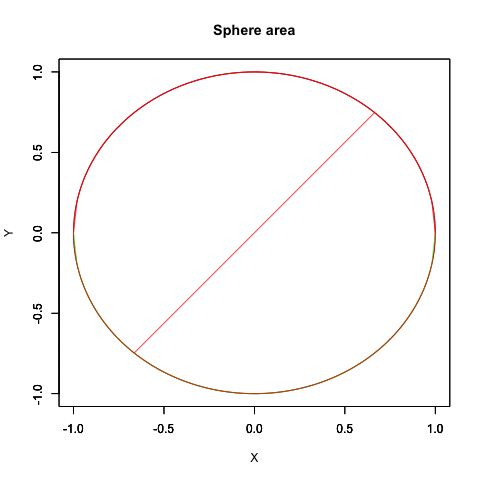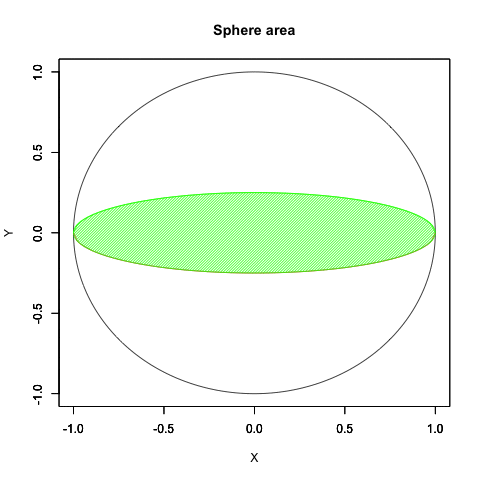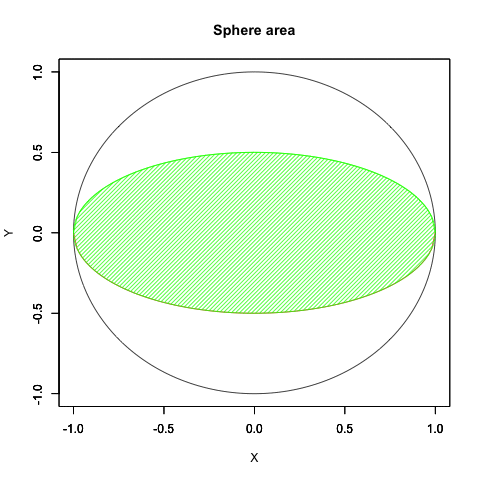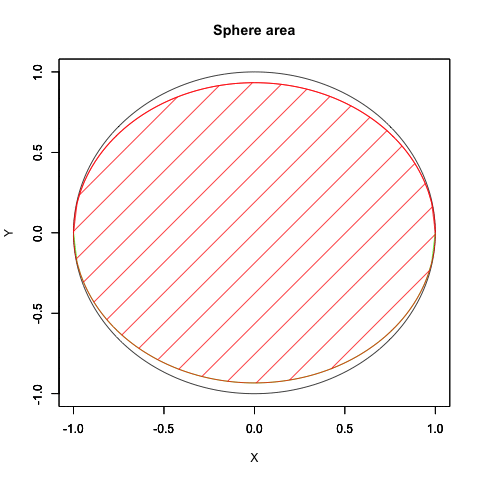
統計言語Rによる検証例(円の面積から球の表面積へ)
#複素平面(球面)
Complex_plane<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_sin<-sin(theta01)
#方向の正負(右が緑、左が赤)
htc=seq(1:360)
cos2<-function(x){cos(2*x/360*2*pi)/2+0.5}
htcval=cos2(htc)
Rotation_ratio<-htcval[c(x)]
htcval_sin=sin(theta)
htcval_cos=cos(theta)*Rotation_ratio
ifelse*1
ifelse*2
f0<-function(x){sqrt(1-x^2)*Rotation_ratio}
f1<-function(x){-sqrt(1-x^2)*Rotation_ratio}
#円弧の描写(ベース)
plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Sphere area", xlab="X", ylab="Y")
par(new=T)#上書き指定
#円弧の描写(回転)
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=C_Top,main="", xlab="", ylab="")
par(new=T)#上書き指定
plot(f1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=C_Bottom,main="", xlab="", ylab="")
#円の塗り潰し
polygon(htcval_sin, #x
htcval_cos, #y
density=c(50*(1-Rotation_ratio)), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=C_Top) #塗りつぶす色
}
#アニメーションさせてみる。library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
統計言語Rによる検証例(合わせ技)
#複素平面(球面)
Complex_plane<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)
theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_sin<-sin(theta01)
#方向の正負(右が緑、左が赤)htc=seq(1:360)
cos2<-function(x){cos(2*x/360*2*pi)/2+0.5}
htcval=cos2(htc)
Rotation_ratio<-htcval[c(x)]
ifelse*3
theta02<-dr[1:x]
ifelse*4
ifelse*5
f0<-function(x){sqrt(1-x^2)*Rotation_ratio}
f1<-function(x){-sqrt(1-x^2)*Rotation_ratio}theta02_cos<-cos(theta02)
ifelse*6, #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=segC) #塗りつぶす色}
#アニメーションさせてみる。library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
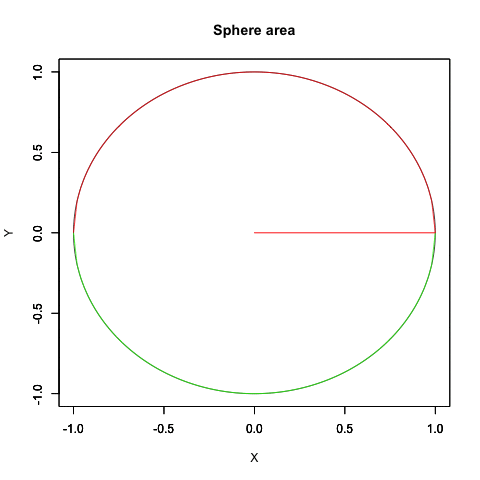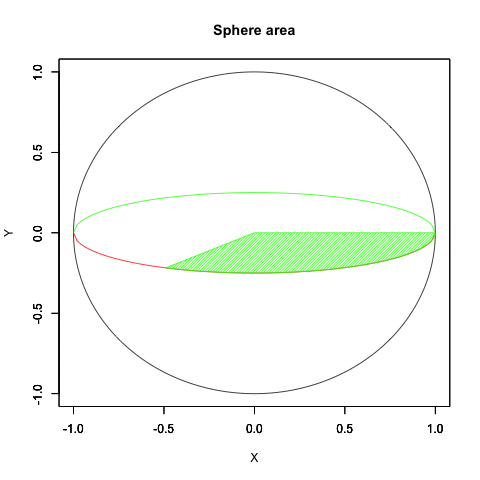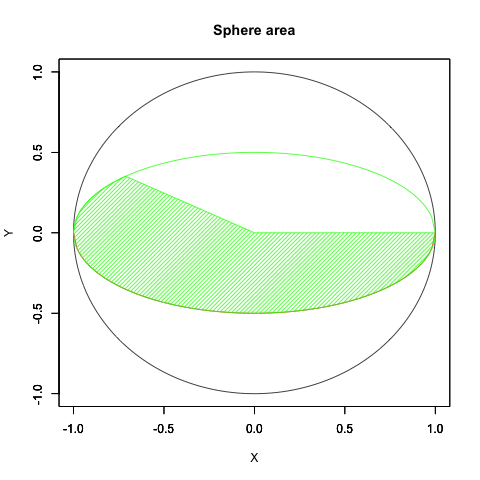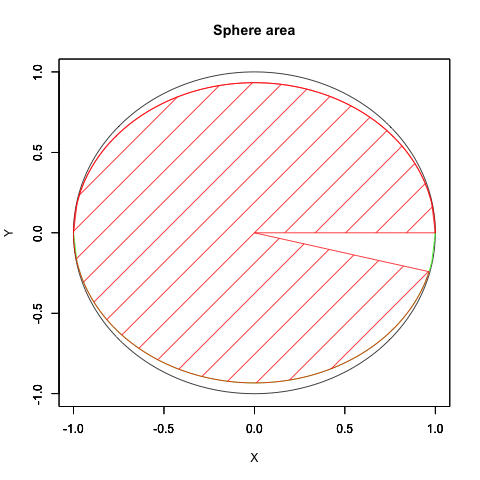
*全然納得がいってないが、今はこれが精一杯…
似た概念を探して「ファインマンの経路積分」に辿り着きました。そもそもファインマン自身、オイラーの公式の絶賛者でしたね。
オイラーの公式(Euler's formula) - Wikipedia
公式の名前は18世紀の数学者レオンハルト・オイラー (Leonhard Euler) に因むが、最初の発見者はロジャー・コーツ (Roger Cotes) とされる。コーツは1714年にlog(cos(x)+sin(xi))=xiを発見したが、三角関数の周期性による対数関数の多価性を見逃した。
1740年頃オイラーはこの対数関数の形での公式から現在オイラーの公式の名で呼ばれる指数関数での形に注意を向けた。指数関数と三角関数の級数展開を比較することによる証明が得られ出版されたのは1748年のことだった。
この公式は複素解析をはじめとする純粋数学の様々な分野や、電気工学・物理学などで現れる微分方程式の解析において重要な役割を演じる。物理学者のリチャード・ファインマンはこの公式を評して「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」だと述べている。
粘菌コンピューターも似た発想の産物ですね。
*1:x%/%90==0 || x%/%90==3),C_Top<-rgb(1,0,0),C_Top<-rgb(0,1,0
*2:x%/%90==0 || x%/%90==3),C_Bottom<-rgb(0,1,0),C_Bottom<-rgb(1,0,0
*3:x%/%90==0 || x%/%90==3),segC<-rgb(1,0,0),segC<-rgb(0,1,0
*4:x%/%90==0 || x%/%90==3),C_Top<-rgb(1,0,0),C_Top<-rgb(0,1,0
*5:x%/%90==0 || x%/%90==3),C_Bottom<-rgb(0,1,0),C_Bottom<-rgb(1,0,0
*6:x%/%90==0 || x%/%90==3),theta02_sin<-sin(theta02)*Rotation_ratio,theta02_sin<-sin(theta02)*-Rotation_ratio)
#円弧の描写
plot(cos(theta), sin(theta), xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Sphere area", xlab="Real Expanse", ylab="Y")
par(new=T)#上書き指定
plot(f0, xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=C_Top,main="", xlab="", ylab="")
par(new=T)#上書き指定
plot(f1, xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=C_Bottom,main="", xlab="", ylab="")
#インジケーター
#segments(cos(dr[x]),sin(dr[x])*Rotation_ratio,0,0,col=segC)
polygon(c(0,theta02_cos), #x
c(0,theta02_sin), #y
density=c(50*(1-Rotation_ratio