いわゆる「放物線」もこの範疇に入る。
放物線(希:παραβολή「parabolē」、羅、英: parabola、独: Parabel) - Wikipedia
その名の通り地表(つまり重力下)で投射した物体の運動(放物運動)が描く軌跡のことであり、 放物線をその対称軸を中心として回転させた曲面を放物面という。数学的な定義としてよく知られたものはいくつかの方法があるが、いずれも適当な枠組みで互いに他を導出することができる等価なものである。
平面幾何学(Euclidean geometry)
準線 (directrix) と呼ばれる直線 L と、その上にない焦点 (focus) と呼ばれる一点 F が与えられるとき、準線 L と焦点 F とをともに含む唯一つの平面 π 上の点 P であって、P から焦点 F への距離 PF と等しい距離 PQ を持つような準線 L 上の点 Q が存在するようなものの軌跡として定義される平面曲線である。
放物線上の点を P(x, y)、焦点を F(0, a)、準線の式を y = -a とすると PQ = PF より以下が成立する。
- y+a=sqrt(x^2+(a-y)^2)
- x^2=4ay
- y^2=4ax(x と y を入れ替えても放物線の方程式として成立する)。
この式は標準形と呼ばれる。
直線に、
l
という名前を付けることがあるように、
平面に
Π
という名前を付けたということです。例えば、
Π:z=0
ならば、
平面Π上の点とは、
xy平面上の点のことです。
円錐曲線
円錐面を母線に平行な平面で切ると、切断面は放物線になる。
この図では円錐面の平面 π による断面(赤い面の縁)が、準線 L と焦点 F をもつ放物線を描くことが確認できる。
二次曲線
二次曲線の一種で、離心率は 1 である。
- 焦点が (0, c)、準線が y = -c のとき、放物線の式 x2 = 4cy となる。
- 焦点が (c, 0)、準線が x = -c のとき、放物線の式は y2 = 4cx となる。
二次関数 y = ax2 + bx + c (a は 0 ではない)が描くグラフは放物線になる。
円錐曲線(二次曲線)の特徴を示す数値のひとつ。円錐曲線、すなわち円・楕円・放物線・双曲線はいずれも、焦点 F からの距離と、準線 d からの距離の比 e が一定となる点の集合である。この比 e が離心率である。
すなわち、円錐曲線上の任意の点 M について、焦点 Fからの距離を FM、準線 d からの距離を MM' と表すとe=FM/MM'となる。円の場合は、楕円での準線を無限遠方においた極限とみなして離心率は0とする。
- 離心率 = 0 … 真円
- 0 < 離心率 < 1 … 楕円
- 離心率 = 1 … 放物線
- 1 < 離心率 … 双曲線
楕円の場合、長径を 2a、短径を 2b とすると焦点同士の距離は2*sqrt(a^2-b^2)となり離心率e=(2*sqrt(a^2-b^2))(2*a)=sqrt*1
②定数(constant)まで備えた二次方程式a*x^2+bx+cの特徴。
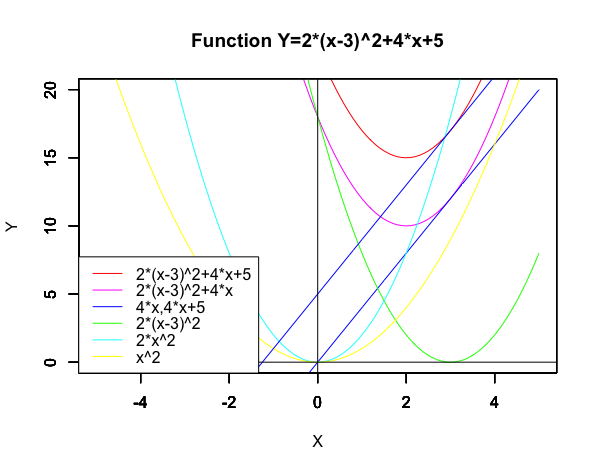
統計言語Rでのコーディング例
#関数定義
f1<-function(x){2*(x-3)^2+4*x+5}
f2<-function(x){2*(x-3)^2+4*x}
f3<-function(x){4*x}
f4<-function(x){2*(x-3)^2}
f5<-function(x){2*x^2}
f6<-function(x){x^2}
f7<-function(x){4*x+5}
#凡例用関数名定義
f1_name<-c("2*(x-3)^2+4*x+5")
f2_name<-c("2*(x-3)^2+4*x")
f3_name<-c("4*x,4*x+5")
f4_name<-c("2*(x-3)^2")
f5_name<-c("2*x^2")
f6_name<-c("x^2")#グラフのスケール決定
gs_x<-c(-5,5)
gs_y<-c(0,20)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"#タイトル定義
Main_title<-c("Function Y=2*(x-3)^2+4*x+5")
x_title<-c("X")
y_title<-c("Y")
#グラフ描画
plot(f1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(f2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f4,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f5,xlim=gs_x,ylim=gs_y,type="l",col=Cyan, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f6,xlim=gs_x,ylim=gs_y,type="l",col=Yellow, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f7,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")#基準線
abline(h=0)
abline(v=0)
#凡例描画legend("bottomleft", legend=c(f1_name,f2_name,f3_name,f4_name,f5_name,f6_name),lty=c(1,1,1,1,1,1),col=c(Red,Magenta,Blue,Green,Cyan,Yellow))

すなわちa*(x-b)^2+c*x+dの意味は…
- a…傾き
- b…引いた数字分だけX軸を+シフト(原点の始まりが遅くなるイメージ)
- c…1時曲線y=xの傾き
- d…足した数字分だけY軸を+シフト
2次方程式の解の公式
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#2次方程式の解の公式yacas("Solve(a*(x-b)^2+c*x+d,x) ")
Yacas vector:
[1] x == (root*2, 2) - (a * (-2 * b) + c))/(2 * a)
[2] x == -(a * (-2 * b) + c + root*3, 2))/(2 * a)
yacas("PSolve(a*(x-b)^2+c*x+d,x) ")
Yacas vector:
[1] (root*4, 2) - (a * (-2 * b) + c))/(2 * a)
[2] -(a * (-2 * b) + c + root*5, 2))/(2 * a)
yacas("PSolve(2*(x-3)^2+4*x+5,x) ")
Yacas vector:
[1] complex_cartesian(2, root(15/2, 2)) complex_cartesian(2, -root(120, 2)/4)
#Rによる計算結果>
a<-2; b<--3; c<-4; d<-5
(sqrt*6/(2 * a)
[1] -1.87868
-(a * (-2 * b) + c + sqrt*7/(2 * a)
sqrt(15/2)
[1] 2.738613
sqrt(120)/4
[1] 2.738613
*計算が合ってない気がするがさて置く
ちなみに...
とりあえず、以下続報…
*1:a^2-b^2)/a^2)である。したがって、楕円形が真円に近いほど離心率は小さな値をとる。
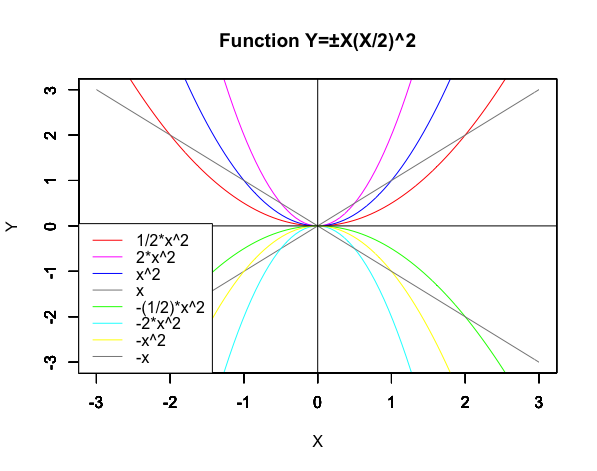
高校数学で扱う範囲は以下。
①±a*x^2(傾きと符号)
統計言語Rでのコーディング例
#関数定義
f1<-function(x){1/2*x^2}
f2<-function(x){2*x^2}
f3<-function(x){x^2}
f4<-function(x){x}
f5<-function(x){-(1/2)*x^2}
f6<-function(x){-2*x^2}
f7<-function(x){-x^2}
f8<-function(x){-x}
#凡例用関数名定義
f1_name<-c("1/2*x^2")
f2_name<-c("2*x^2")
f3_name<-c("x^2")
f4_name<-c("x")
f5_name<-c("-(1/2)*x^2")
f6_name<-c("-2*x^2")
f7_name<-c("-x^2")
f8_name<-c("-x")#グラフのスケール決定
gs_x<-c(-3,3)
gs_y<-c(-3,3)
#グラフの色の決定
Black<-rgb(0,0,0)
Red<-rgb(1,0,0)
Magenta<-rgb(1,0,1)
Blue<-rgb(0,0,1)
Green<-rgb(0,1,0)
Cyan<-rgb(0,1,1)
Yellow<-rgb(1,1,0)
Gray<-"#888888"#タイトル定義
Main_title<-c("Function Y=±X(X/2)^2")
x_title<-c("X")
y_title<-c("Y")
#グラフ描画
plot(f1,xlim=gs_x,ylim=gs_y,type="l",col=Red, main=Main_title,xlab=x_title,ylab=y_title)
par(new=T)#上書き指定
plot(f2,xlim=gs_x,ylim=gs_y,type="l",col=Magenta, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f3,xlim=gs_x,ylim=gs_y,type="l",col=Blue, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f4,xlim=gs_x,ylim=gs_y,type="l",col=Gray, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f5,xlim=gs_x,ylim=gs_y,type="l",col=Green, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f6,xlim=gs_x,ylim=gs_y,type="l",col=Cyan, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f7,xlim=gs_x,ylim=gs_y,type="l",col=Yellow, main="",xlab="",ylab="")
par(new=T)#上書き指定
plot(f8,xlim=gs_x,ylim=gs_y,type="l",col=Gray, main="",xlab="",ylab="")#基準線
abline(h=0)
abline(v=0)
#凡例描画legend("bottomleft", legend=c(f1_name,f2_name,f3_name,f4_name,f5_name,f6_name,f7_name,f8_name),lty=c(1,1,1,1,1,1,1,1),col=c(Red,Magenta,Blue,Gray,Green,Cyan,Yellow,Gray
*2:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d
*3:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d
*4:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d
*5:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d
*6:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d))) - (a * (-2 * b) + c
*7:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d))))/(2 * a)
[1] -6.12132
sqrt((a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d))) - (a * (-2 * b) + c



