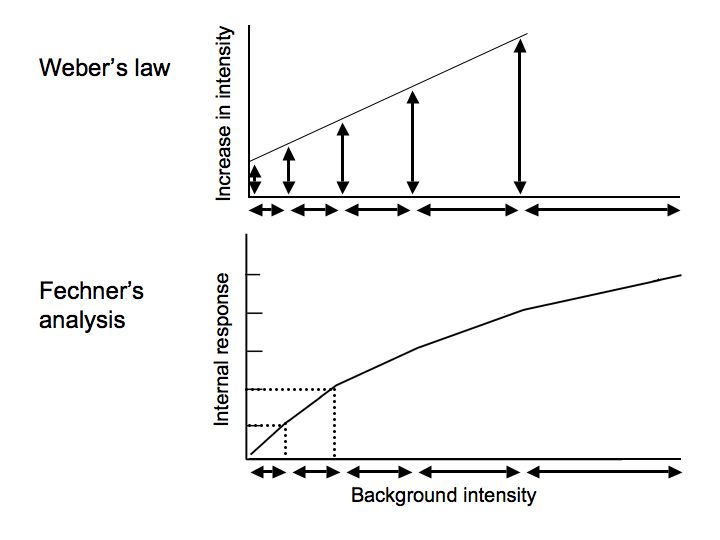
人間はある周波数[Hz]の音を聞いていたとき、その2倍の周波数[Hz]の音を聞くと音の高さが2倍になったように感じます。言い換えると、周波数の対数を取ったものを横軸とし、縦軸に人間が感じる音の高さをプロットすると直線になるのです。これは精神物理学者が実験で確かめた人間の特性で心理学者ヴエーバ・フェヒナの法則(Weber–Fechner law)と呼ばれています。
感覚に関する精神物理学の基本法則で、心理的感覚Sと刺激の物理的強度Iの間にS=Klog(I)(ここでKは定数)の非線形関係がある事を実証した。中等度の刺激について五感のすべてに近似を与える事で知られる。
ヴェーバーの法則
エルンスト・ヴェーバー(Ernst Heinrich Weber、1795年〜1878年)は、1834年に錘を持ち上げる実験を行い、錘の重さの変化を感じ取る感覚は、何g増えたかといった差ではなく、何倍になったかという比に依存していることを「Zusätze zur Lehre vom Bau und von der Verrichtung der Geschlechtsorgane(1846年)」や「Die Lehre vom Tastsinn und Gemeingefühl(『触覚と一般感覚』1851年)」で発表。
それによれば刺激の弁別閾(threshold、丁度可知差異:気づくことができる最小の刺激差)は、基準となる基礎刺激の強度に比例する。
はじめに加えられる基礎刺激量の強度をR とし、これに対応する識別閾値をΔR とすると、Rの値にかかわらずΔR/R=constant(定数)が成り立つ。この一定の値をヴェーバー比(Weber ratio)という。統計言語Rによる検証例
f0<-function(x){(1/2)*x+8}
plot(f0,xlim=c(0,64),ylim=c(0,32),type="l",col=rgb(0,0,0), main="Weber's Low",xlab="Background Intencity",ylab="Increase intensity")#第一区間(0-1)
tc <- seq(0, 1, length=10) #0から1までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(0,tc,1), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色#第2区間(1-3)
tc <- seq(1, 3, length=10) #1から2までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(1,tc,3), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,1)) #塗りつぶす色#第3区間(3-8)
tc <- seq(3, 8, length=10) #3から8までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(3,tc,8), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#第4区間(8-16)
tc <- seq(8, 16, length=10) #8から16までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(8,tc,16), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色#第5区間(16-32)
tc <- seq(16, 32, length=10) #16から32までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(16,tc,32), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,1)) #塗りつぶす色
#第6区間(32-64)
tc <- seq(32, 64, length=10) #32から64までを10等分
tcvals <- f0(tc) #それぞれの縦軸の値
polygon(c(32,tc,64), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,1,0)) #塗りつぶす色
たとえば、100の刺激が110になったときはじめて「増加した」と気付くならば、200の刺激が210に増加しても気付かず、気付かせるためには220にする必要がある。
ウェーバー比はたとえば,音の強さについては 11分の1,圧覚では7分の1になる。
【ブリタニカ国際大百科事典】広義にはやっと意識される境界刺激のこと。厳密には刺激を量的ないし質的に変化させた場合,ある特定の反応がそれとは異なった反応へと (またはある経験がそれとは異なった経験へと) 転換する,その境目の刺激尺度上の点のこと,ないしはこのような反応の転換の現象をさす。一般にはこのような転換点は,特定の反応が 50%の確率で生起する刺激量として統計的に定められる。なお刺激を小さくした場合に,反応が生じるか生じないか (知覚が生じるか生じないか) の境目に対応する刺激量を刺激閾ないし絶対閾といい,標準となる刺激をわずかに変化させた場合に,もとの標準刺激に対するものとは異なった反応が生じるか生じないか (その差異に気づくか気づかないか) の境目に対応する刺激量を弁別閾 (丁度可知差異) という。
【小学館デジタル大辞泉】原義は、門の敷居。心理学で、ある感覚や同種の刺激の相違を感知できるか否かの境目。また、その刺激量。→刺激閾(しげきいき) →弁別閾(べんべついき)【株式会社平凡社百科事典マイペディア】刺激の連続的変化に対して,その知覚や判断のあり方が突然転換する限界。その時の刺激の最小値を閾値という。たとえば刺激の存在を初めて認知できる点は刺激閾(絶対閾),刺激の増加や減少が初めて明瞭な量的変化として感じられる点は弁別閾という。
【世界大百科事典 第2版】〈しきい〉ともいう。通常,反応を起こすのに最小必要限の刺激の強さをいい,その値を閾値という。閾以下の強さの刺激(閾下刺激)では反応は起こらない。たとえば,網膜に視覚感覚を起こす最小の光の強さなどであるが,刺激によって反応を起こす種類の現象一般に用いられる言葉である。閾値は刺激の物理的な性質や時間経過によっても変化する。また反応する側の種々の内部要因によっても変わる。たとえば,同じ刺激が繰り返し与えられると,閾値が上がり,反応が起こらなくなるし,また逆にその刺激が長い間与えられず,反応の動機づけ(いわゆる衝動)が高まってくると,閾値が低下する。
フェヒナーの法則
ヴェーバーの弟子でその研究を発展させ精神物理学という学問を創始し、実験心理学の成立に大きな影響を与えたグスタフ・フェヒナー(Gustav Theodor Fechner、1801年〜1887年)は、ヴェーバーの法則の式を積分することにより、以下の対数法則を導き出した。
*ここでΔR をdR として積分することは若干の飛躍があり、厳密な計算ではなく近似である。
統計言語Rによる実証例#汎用計算機代数ソフトウェアYacas使用
library(Ryacas)
yacas("Integrate(x) a/x")
expression(a * log(x))刺激量の強度R が変化する時、これに対応する感覚量E はE=C*log(R)(ここでCは定数)の関係となる。つまり心理的な感覚量は、刺激の強度ではなく、その対数に比例して知覚される。
統計言語Rによる検証例
f1<-function(x){log(x)+8}
plot(f1,xlim=c(0,64),ylim=c(0,16),type="l",col=rgb(0,0,0), main="Fechner's amnalysis",xlab="Background intencity",ylab="Internal Respnce")#第一区間(0-1)
tc <- seq(0.0001, 1, length=10) #0から1までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(0.0001,tc,1), #x
c(0.0001,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色#第2区間(1-3)
tc <- seq(1, 3, length=10) #1から2までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(1,tc,3), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,1)) #塗りつぶす色#第3区間(3-8)
tc <- seq(3, 8, length=10) #3から8までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(3,tc,8), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#第4区間(8-16)
tc <- seq(8, 16, length=10) #8から16までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(8,tc,16), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色#第5区間(16-32)
tc <- seq(16, 32, length=10) #16から32までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(16,tc,32), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,1)) #塗りつぶす色
#第6区間(32-64)
tc <- seq(32, 64, length=10) #32から64までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(32,tc,64), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,1,0)) #塗りつぶす色
フェヒナーの法則と呼ばれることも多いが、ヴェーバーの法則から導出したことからヴェーバー・フェヒナーの法則とも呼ばれる。たとえば、100の刺激が倍に増加して200になるときの感覚量と、200の刺激が倍に増加して400になるときの感覚量の変化は等しい。
風変わりな人物であり、太陽を見た後の残像を研究するために太陽を肉眼で観察して失明状態になりかけたこともあった。
その哲学思想は、精神と物質はひとつであり宇宙は一つの面から見れば意識、一つの面から見れば物質であるというものである。彼は宇宙を意識的存在と見ることを「昼の見方」、無生物として見ることを「夜の見方」と呼び、夜の見方の眠りに落ちた人々を昼の見方に目覚めさせることを目指した。彼の哲学の反響は小さかったが、その哲学に基づいて構想された、身体と精神(物的エネルギーと心的強度)の関係を研究する精神物理学は大きな反響を呼んだのである。
出発点は、まずここ。案外、以下の話と絡んでくるかもしれないのです。
対数関数(Logarithm Function)x=±a(1/a)^yあるいはy=±log(x,base=a(1/a))ではなく、指数関数(Exponential Function)y=±a(1/a)^xだけが文字通り「指数級的(Exponential)展開」による「 有意味な増大(SI=Significant increase)」や「有意味な減少(SR=Significant reduction)」と「無視可能な状態(IS=Ignorable State)」の往復を提示する。増大率上限e^1=e(2.718282)、標準失敗率e^-1=1/e(0.3678794)、標準成功率1-e^-1(0.6321206)の世界?
- y=a^x…「無視可能な状態(IS=Ignorable State)」から「 有意味な増大(SI=Significant increase)」へ。転回点は座標[0,1]あるいは複素座標Cos(π/2=0)+Sin(π/2=1)i=0+1iとなる。
- y=(1/a)^x…「有意味な減少(SR=Significant reduction)」から「無視可能な状態(IS=Ignorable State)」へ。転回点は同様に座標[0,1]あるいは複素座標Cos(π/2=0)+Sin(π/2=1)i=0+1iとなる。
- y=-a^x…「無視可能な状態(IS=Ignorable State)」から「有意味な減少(SR=Significant reduction)」へ。転回点は座標[0,-1]あるいは複素座標Cos(-π/2=3/4π=0)+Sin(-π/2=3/4π=-1)i=0+-1iとなる。
- y=-(1/a)^x…「 有意味な増大(SI=Significant increase)」から「無視可能な状態(IS=Ignorable State)」へ。転回点は同様に座標[0,-1]あるいは複素座標Cos(-π/2=3/4π=0)+Sin(-π/2=3/4π=-1)i=0+-1iとなる。
ただし実際の自然界に対する観測においてはロジスティック方程式を意識せねばならない局面も存在するから要注意である。
とりあえず音楽方面ではロジスティック方程式は登場しない様なんです?
音楽で使う音の高さを世界共通で扱うために決めた特定の周波数を標準高度と呼ぶ。古くからいろいろな標準高度が使われてきたけど、19世紀末からはパリ会議(1859年)とウィーン会議(1885年)によって、オクターブ4のラ(A)の音を435Hzとする標準高度が代表的に使われるようになった。しかし、現在ではシュトゥットガルト会議(1834年)で決められたオクターブ4のラ(A)の音を440Hzとする標準高度が演奏会高度やMIDIなどコンピュータを使ったDTM(Desktop Music) の基準として広く使われている。
- この基準周波数を少し高くして441Hzにすると音が全体的に少し高くなる分、音楽が明るくなったような印象を受けるので、演奏家などの注文によって440Hzでなく、441Hzや442Hz、あるいは439Hzで調律して欲しいという要望に応じて調整することもある。
この様にオクターブとはある音からその2倍の高さの音に聞こえる音の範囲を表しているが、オクターブずつ離れた音だけでは音の数が少なすぎて音楽を作るのに不十分である。そこで、1オクターブ内にいくつかの音を作り出し、それらの音に名前(音名)を与える。音楽で普通使われる音名はドレミファソラシドである。ドレミファソラシドはピアノの白鍵の音で、幹音と言われる。国によって違った言い方もあるが、1オクターブ内でこれらの音を使うのは西洋音楽をはじめとして世界の主流になっている。音を絶対的に指定する場合には「オクターブ4のラのシャープ(A#4)」というように指定する。
音再生ルーチン(Win/Mac共用)
library(tuneR)
#音再生ルーチン(Win/Mac振り分け)
#ちなみにWindowsの場合は、Sys.info()["sysname"] == "windows"
ex_play<-function(song){
if(Sys.info()["sysname"] == "Darwin"){
filename <- tempfile("tuneRtemp", fileext = ".wav")
writeWave(song, filename)
system(paste("open -a iTunes", filename))
return(invisible())
}else{
play(song)
return(invisible())
}}
#サンプル再生例
beep<- sine(440)
ex_play(beep)
Macで"/wav"ファイルを鳴らすもっとスマートな方法
library(tuneR)
#Rであらかじめ以下を入力
setWavPlayer("/usr/bin/afplay")
#サンプル再生例
beep<- sine(440)
ex_play(beep)
Do,Re, Mi,Fa,Sol, Laは、なんとなくドイツ語かな、と思っていましたが実はラテン語です。聖ヨハネ賛歌というラテン語の曲があり、この曲では各小節の頭の音が、C, D, E, F, G, Aになっています。該当する音のラテン語の歌詞は、「Ut」「Resonare」「Mira」「Famuli」「Solve」「Labii 」となっていますので、そこから音をとり、「Ut」「Re」「Mi」「Fa」「So」「La 」となり、「Ut」は言いにくいので「Do」となったということです。
第7節の2つの単語の頭をとると、「SJ」ですが、JはIの異体字であり、「Johannes」はフランス語で「Ian」なので、「Si」になりました。こうして、イタリア語の音名「ドレミファソラシド」ができあがったのです。
統計言語Rによる作表例
#世界各国の音階表示
american_and_british<-c("C","C#=D♭","D","D#=E♭","E","E#=F","F","G","G#=A♭","A","A#=B♭","B")
german<-c("C","Cis=Des","D","Dis=Ees","E","Eis=Fes","F","G","Gis=Aes","A","Ais=Hes","H")
italian<-c("Do","Do#=Re♭","Re","Re#=Mi♭","Mi","Mi#=Fa♭","Fa","So","So#=Ra♭","Ra","Ra#=Si♭","Si")
french<-c("Do(Ut)","Do(Ut)dièse=Re bémol","Re","Re dièse=Mi bémol","Mi","Mi dièse=Fa bémol","Fa","So","So dièse=Ra bémol","Ra","Ra dièse=Si bémol","Si")
japanese<-c("イ(I)","嬰イ(I)=変ロ(Ro)","ロ(Ro)","嬰ロ(Ro)=変ハ(Ha)","ハ(Ha)","嬰ハ(Ha)=変ニ(Ni)","ニ(Ni)","ホ(Ho)","嬰ホ(Ho)=変ヘ(He)","ヘ(He)","嬰ヘ(He)=変ト(To)","ト(To)")
Music_scales<-data.frame(American_and_British=american_and_british, German=german,Italian=italian,French=french,Japanese=japanese)
library(xtable)
print(xtable(Music_scales), type = "html")
| American_and_British | German | Italian | French | Japanese | |
|---|---|---|---|---|---|
| 1 | C | C | Do | Do(Ut) | イ(I) |
| 2 | C#=D♭ | Cis=Des | Do#=Re♭ | Do(Ut)dièse=Re bémol | 嬰イ(I)=変ロ(Ro) |
| 3 | D | D | Re | Re | ロ(Ro) |
| 4 | D#=E♭ | Dis=Ees | Re#=Mi♭ | Re dièse=Mi bémol | 嬰ロ(Ro)=変ハ(Ha) |
| 5 | E | E | Mi | Mi | ハ(Ha) |
| 6 | E#=F | Eis=Fes | Mi#=Fa♭ | Mi dièse=Fa bémol | 嬰ハ(Ha)=変ニ(Ni) |
| 7 | F | F | Fa | Fa | ニ(Ni) |
| 8 | G | G | So | So | ホ(Ho) |
| 9 | G#=A♭ | Gis=Aes | So#=Ra♭ | So dièse=Ra bémol | 嬰ホ(Ho)=変ヘ(He) |
| 10 | A | A | Ra | Ra | ヘ(He) |
| 11 | A#=B♭ | Ais=Hes | Ra#=Si♭ | Ra dièse=Si bémol | 嬰ヘ(He)=変ト(To) |
| 12 | B | H | Si | Si | ト(To) |
オクターブの上限と下限
普通音楽で使われるオクターブは0から8ぐらいまでである。88鍵ピアノは27.5Hz~4096Hzまで出せ、オクターブ0から7の途中までとなる。
- オクターブ0のラ(A)の音の周波数は27.5Hzであり、どうせそれより低いオクターブ-1を作っても人間にはほとんど聞こえない。
- オクターブ8以上の音は実際には聞くことができるが音楽ではあまり使われない。オクターブ10のラ(A)の音の周波数は28160Hzであり、人間には聞こえないと言ってよい。
また、MIDIでは鍵盤の数が0から127であり、ノートナンバー(鍵盤番号)127の周波数は42192.3Hzであり、人間には全然聞こえないと言ってよいから、これ以上の番号を用意する必要がない。ちなみに、このようにノートナンバーで音を指定する場合、ギターなどの弦楽器で滑らかに音の高さを変化させる演奏(ポルタメント奏法と言う)は再現できないのではないかと思うかもしれないが、そんな心配は御無用で、ポルタメント奏法を指定する命令もあるからMIDIはいろいろな楽器に対応できる。
統計言語Rによる検証例
f1<-function(x){440*2^x}
plot(f1,xlim=c(-4,4),ylim=c(0,4000),type="l",col=rgb(0,0,0), main="Music Scale",xlab="Octave",ylab="Hz")
#第一区間(2^-4(27.5Hz)~2^-3(55.0Hz))
tc <- round(seq(-4,-3,length=10)) #0から1までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-4,tc,-3), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,0)) #塗りつぶす色
#第2区間(2^-3(55.0Hz)~2^-2(110Hz))
tc <- seq(-3, -2, length=10) #1から2までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-3,tc,-2), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,0,1)) #塗りつぶす色
#第3区間(2^-2(110Hz)~2^-1(220Hz))
tc <- seq(-2, -1, length=10) #3から8までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-2,tc,-1), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,1)) #塗りつぶす色
#第4区間(2^-1(220Hz)~2^0(440Hz))
tc <- seq(-1, 0, length=10) #8から16までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(-1,tc,0), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
#第5区間(2^0(440Hz)〜2^1(880Hz))
tc <- seq(0, 1, length=10) #16から32までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(0,tc,1), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,1)) #塗りつぶす色
#第6区間(2^2(1760Hz)~2^3(1760Hz))
tc <- seq(1, 2, length=10) #32から64までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(1,tc,2), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(1,1,0)) #塗りつぶす色
#第8区間(2^3(3520Hz)~2^4(4186Hz))
tc <- seq(3, 4, length=10) #32から64までを10等分
tcvals <- f1(tc) #それぞれの縦軸の値
polygon(c(3,tc,4), #x
c(0,tcvals,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,0,0)) #塗りつぶす色

#音階の対数表現
music_scale<-c("C","C#=D♭","D","D#=E♭","E","F","F#=G♭","G","G#=A♭","A","A#=B♭","B")
frequency<-c("2^0","2^(1/12)","2^(2/12)","2^(3/12)","2^(4/12)","2^(5/12)","2^(6/12)","2^(7/12)","2^(8/12)","2^(9/12)","2^(10/12)","2^(11/12)")
approximation<-c("1.000000","1.059463","1.122462","1.189207","1.259921","1.33484","1.414214","1.498307","1.587401","1.681793","1.781797","1.887749")
scale_calculation<-data.frame(Music_Scale=music_scale, Frequency=frequency,Approximation=approximation)
library(xtable)
print(xtable(scale_calculation), type = "html")
| Music_Scale | Frequency | Approximation | |
|---|---|---|---|
| 1 | C | 2^0 | 1.000000 |
| 2 | C#=D♭ | 2^(1/12) | 1.059463 |
| 3 | D | 2^(2/12) | 1.122462 |
| 4 | D#=E♭ | 2^(3/12) | 1.189207 |
| 5 | E | 2^(4/12) | 1.259921 |
| 6 | F | 2^(5/12) | 1.33484 |
| 7 | F#=G♭ | 2^(6/12) | 1.414214 |
| 8 | G | 2^(7/12) | 1.498307 |
| 9 | G#=A♭ | 2^(8/12) | 1.587401 |
| 10 | A | 2^(9/12) | 1.681793 |
| 11 | A#=B♭ | 2^(10/12) | 1.781797 |
| 12 | B | 2^(11/12) | 1.887749 |
「ドレミファソラシド、ドシラソファミレド」再生例
library(tuneR)
f1<-function(x){(440*2^(-3/12))*2^x} #チューンダウン
c0<-f1(c(0,2/12,4/12,5/12,7/12,9/12,11/12,1))
c1<-c(c0,rev(c0))
for (i in c1) {
beep<- sine(i);
play(beep)
}#参考
c0
[1] 440.0000 493.8833 554.3653 622.2540 659.2551 739.9888 830.6094 880.0000
もちろん「聴覚」だけでなく「視覚」も対数表現の影響下に…