このサイトが準拠する時空論の中枢。

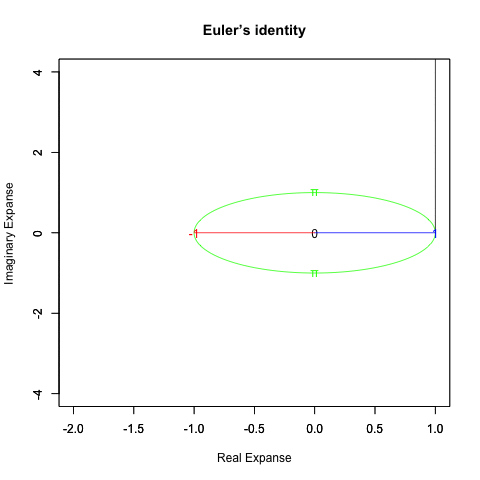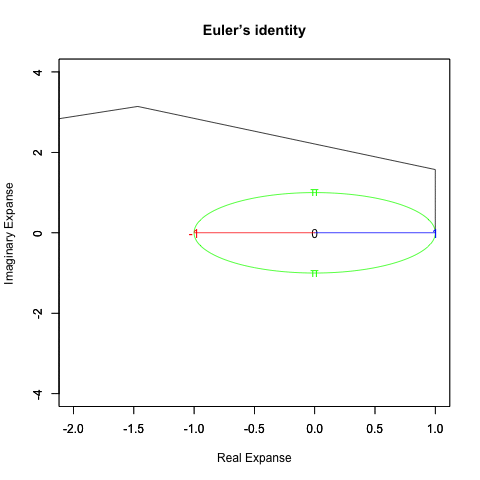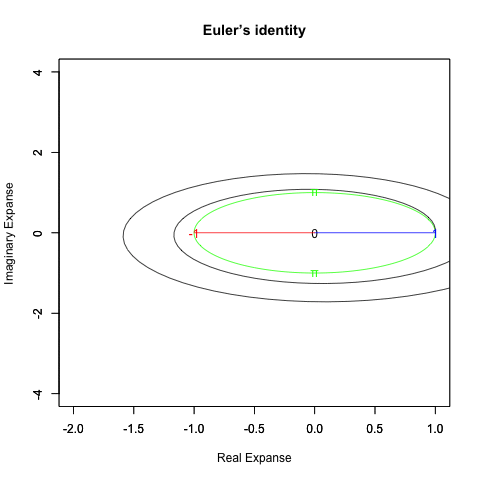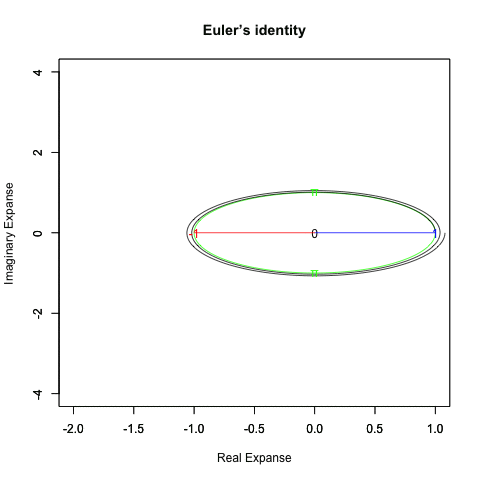
①まず任意の観測原点「0」を想定する。有意の観測結果を得るまでは何も起こらない(一切の間隔尺度が構築区可能なので時間も空間も認識不可能)。
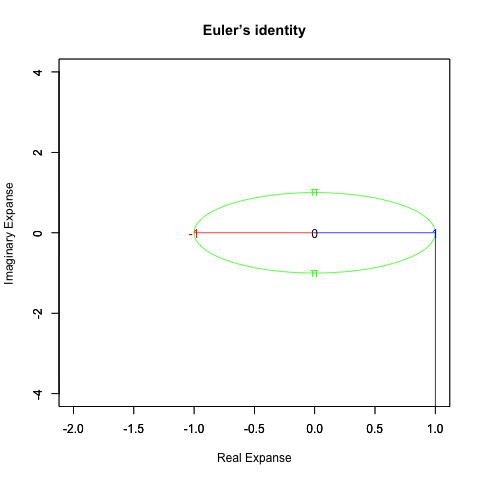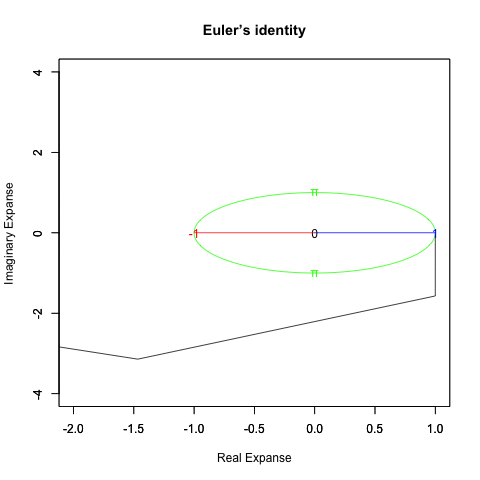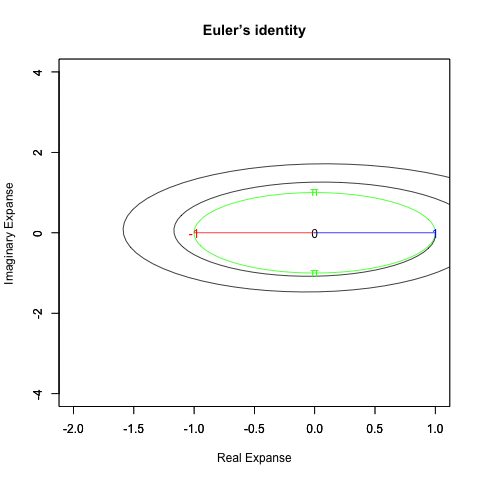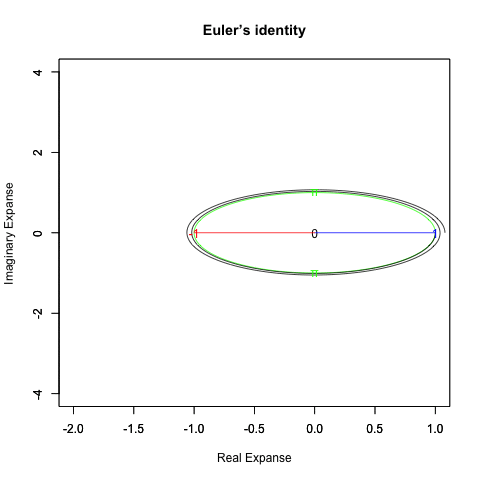
*幾何学的には円柱/球の表面にしか存在し得ない正01角形の世界に対応。②何らかの有意な観測結果が得られると初めて「0=観測原点たる自分」「1=観測対象との距離(前)」「−1=観察対象の座標上の対蹠」「π=対蹠に至る直線距離以外のルート」「t=かかる空間定義と可換性を有する観測間隔」なる基準から出発する、原始的なある種の極座標系(Polar coordinates system)時空間認識が成立し、最初の「仮想世界(Virtual world)=観測原点をすっぽり包む全球型スクリーン」の構築が可能となる。とりあえずこれを「オイラーの原始量(Euler's primitive sweep)」と呼ぶ。
*幾何学的には円柱/球の表面にしか存在し得ない正02角形の世界に対応。*この時点で初めて微積分的解析の可能性が開かれる。
③「オイラーの原始量(Euler's primitive sweep)」はオブジェクト志向言語における多重クラス設計/生成されたオブジェクトの多重参照の様な形で系統発生(Phylogeny)を繰り返してきたが、直交座標系(Rectangular coordinate system/Orthogonal coordinate system)へのパラダイムシフト(Paradigm Shift)といった重要な発想の飛躍には以下の条件が揃う必要があったと想定される(人類に至る以前に下された判断で、人類はそれを継承しただけとも)。
- 「オイラーの原始量(Euler's primitive sweep)」において既に時間と空間で生じている様な直交性(線的独立性)の空間尺度間における確認。例えば基本円(Unit Circle=半径1の円弧)に内接する多角形のうち、これが検出可能なのは上掲の正2角形=「オイラーの原始量(Euler's primitive sweep)」と正方形と基本円そのものに限られ、ここから「等速円運動(Constant velocity circular motion)の法則(等速円運動をX軸から観測するとCos波、Y軸から観察するとSin波が得られ、両者を再合成すると円を描く)」あるいはオイラーの公式e^θi=cos(θ)+sin(θi)(理論的期待値)=(1±θi/N)^N(大数弱の法則に基づく無限接近の可能性の示唆/到達不可能性の明示)が必然的に組み込まれる。ちなみにこうした過程で人類は「右手系」か「左手系」かの選択を迫られて前者を選んでいる。
- 片対数尺概念導入による等比数列的尺度から等差数列的尺度への変換
- 音楽理論や透視図法的発想に基づく等差数列的尺度から等比数列的尺度への変換
音楽理論透視図法
④かかる時空間認識が何らかの形での「(自らの生存手段と深く結びついた)有意味な観測結果」に立脚するものである以上、その決定的喪失は「原則的には(In principle)」当事者の死滅、あるいはかかる時空間認識概念そのものの放棄に結びつく。とはいえ実際には「(オブジェクト志向言語における)多重化されたクラス関係」や「(オブジェクト志向言語における)多重化されたオブジェクト間参照」の調整だけで乗り切るケースが多い。つまり我々の歴史的記憶はリアルタイムで改竄され続けている。
【参照】「フーリエ解析(Fourier Analysis)」との対応
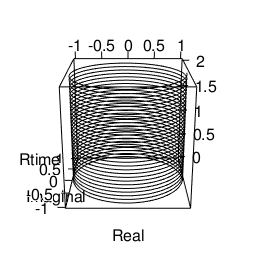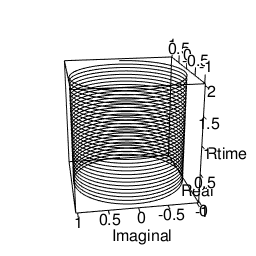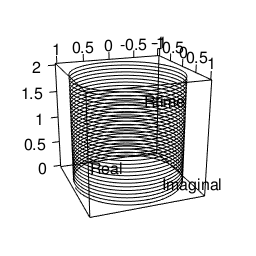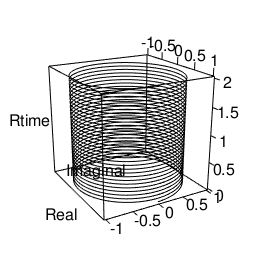
基本円柱(Unit Cylinder)e^θi^tを2Dヒストグラムに掛けてみると以下の様になる。
- XY軸…出現度数1以上(周回数が増えるほど増加し平均が1に近付く)の円弧
- XZ軸…出現度数1以上(周回数が増えるほど増加し平均が1に近付く)のCos波
- YZ軸…出現度数1以上(周回数が増えるほど増加し平均が1に近付く)のSin波
- 「半径分の長さ1の線分の(分割分だけの)集合」なる検出方法もある。
「あらゆる波形を正弦波の足し合わせで表現する」フーリエ解析は、基本円柱(Unit Cylinder)への一時的干渉によって有限の「有意味な観測結果」を生成する。
この時の複素数空間(complex n-space)上のXY(円弧)面。
何故「一時的干渉による有限の結果」しか残せないかというと、基本的に視野拡大(サンプル数増大)による大数の法則(LLN=Law of Large Numbers)や中心極限定理(CLT=Central Limit Theorem)の影響力増大、及び時間的減衰による干渉力の減少などによる「基本円柱(Unit Cylinder)e^θi^t状態(確率論的には正規分布の世界)への回帰」を完全に防ぐ方法などこの世には存在しないからである。
*そう、参照する周期など増やそう思えば無限に増やせるし、あらゆる「干渉」は時間的減衰を意識する必要があるのである。
こうした考え方を一言で要約すると「諸行無常」となります。さらには厳密に考え様とすればするほど実在と非在の境界線が曖昧となる「色即是空、空即是色」の世界でもあり、境界線の見極めに「ロジスティック回帰分析(
Logistic regression analysis)」や「マルコフ連鎖モンテカルロ法(MCMC=Markov chain Monte Carlo methods)の様な特殊な技法を駆使する必要が生じるのです。


20世紀後半における人工知能ブームを祖型として派生した「オブジェクト指向プログラミング(OOP=Object-Oriented Programming)技法」はある意味、こうした(コーディング工程効率化の妨げとなる)事象の諸行無常性への対抗手段として発展してきたといえましょう。
オブジェクト指向プログラミング(OOP=Object-Oriented Programming)の特徴
①厳密な名前空間定義管理によるクラス構成の(可能な限りの)一貫性維持…それぞれは親クラスからの継承の連鎖の形で定義されており、必要に応じた改変を加えられ続けるが、その影響が(プログラム中で実際に参照される)具象クラスに及ばない様に最大限の配慮が為される。
②オブジェクトの参照数管理…実際のプログラム中で具象クラスから生成されるオブジェクトは、最初に参照されるまで存在せず、かつ参照数が0になると自動的に消滅する事でメモリ利用の効率化が果たされる。
③カプセル化による処理内容の分割と全体像を俯瞰するメタ視点保持の必然性の発生…厳密な名前空間定義管理の要諦は、カプセル化によるそれぞれの処理内容の完全分割(互いにその存在を意識する必要がなくなる工夫)なのだが、クラス全体に必要に応じた改変を加え続けるには、その制約を超越したメタ視点が保持され続けなければならない。
以下続報…