
三角関数は微分する都度時計回りに90度回転し4回で1周します。
統計言語Rによる検証例
#コサイン関数
D01<-expression(cos(x))
D(D01,"x")
-sin(x)
D01<-expression(-sin(x))
D(D01,"x")
-cos(x)
D01<-expression(-cos(x))
D(D01,"x")
sin(x)
D01<-expression(sin(x))
D(D01,"x")
cos(x)
#サイン関数D01<-expression(sin(x))
D(D01,"x")
cos(x)D01<-expression(cos(x))
D(D01,"x")
-sin(x)
D01<-expression(-sin(x))
D(D01,"x")
-cos(x)
D01<-expression(-cos(x))
D(D01,"x")
sin(x)
統計言語Rによる作表例
#ガウス平面上における遷移図
target_angles<-c("0(2π)radian/0(360)degree","π/2radian/90degree","πradian/180degree ","3/4πradian/270degree")imaginary_solution<-c("1+0i","0+0i","-1+0i","0-0i")
cosine_function<-c("cos(x)","sin(x)","-cos(x)","-sin(x)")
sine_function<-c("sin(x)","-cos(x)","-sin(x)","cos(x)")
Days_of_Future_Past_F<-data.frame(Angles=target_angles, Imaginary_solution=imaginary_solution, Cosine=cosine_function, Sine=sine_function)
library(xtable)
| Angles | Imaginary_solution | Cosine | Sine | |
|---|---|---|---|---|
| 1 | 0(2π)radian/0(360)degree | 1+0i | cos(x) | sin(x) |
| 2 | π/2radian/90degree | 0+0i | sin(x) | -cos(x) |
| 3 | πradian/180degree | -1+0i | -cos(x) | -sin(x) |
| 4 | 3/4πradian/270degree | 0-0i | -sin(x) | cos(x) |
まぁ「90度位相がズレてるだけで同じ波」ですからね。それぞれを統計言語R上からYacasでマクローリン展開するとこんな感じ。
Yacas (ˈjækəs, やかす) - Wikipedia
GNU General Public License にしたがった利用と配布が認められているフリーソフトウェアの汎用計算機代数ソフトウェアで、名前は Yet Another Computer Algebra System から来ている。
計算機代数の演算を行うシステムであるため、数式の記号操作ができる。また記号計算および任意精度の数値計算を行うための独自のプログラミング言語処理系を備えている。多くの数式処理操作を実装したスクリプトのライブラリを持っており、新たに実装したアルゴリズムの追加が容易に行えるようになっている。スクリプト言語および実装されている機能とアルゴリズムについての文書が多数用意されている。
テイラー展開(Taylor expansion)とマクローリン展開(Maclaurin expansion) - Wikipedia
数学において、テイラー級数 (Taylor series) は関数のある一点での導関数たちの値から計算される項の無限和として関数を表したものである。そのような級数を得ることをテイラー展開という。
テイラー級数の概念はスコットランドの数学者ジェームズ・グレゴリーにより定式化され、フォーマルにはイギリスの数学者ブルック・テイラーによって1715年に導入された。0 を中心としたテイラー級数は、マクローリン級数 (Maclaurin series) とも呼ばれる。これはスコットランドの数学者コリン・マクローリンにちなんでおり、彼は18世紀にテイラー級数のこの特別な場合を積極的に活用した。
関数はそのテイラー級数の有限個の項を用いて近似することができる。テイラーの定理はそのような近似による誤差の定量的な評価を与える。テイラー級数の最初のいくつかの項として得られる多項式はテイラー多項式と呼ばれる。関数のテイラー級数は、その関数のテイラー多項式で次数を増やした極限が存在すればその極限である。関数はそのテイラー級数がすべての点で収束するときでさえもテイラー級数に等しいとは限らない。開区間(あるいは複素平面の開円板)でテイラー級数に等しい関数はその区間上の解析関数と呼ばれる。
階乗計算については以下。
全体構造を要約するとこういう感じ。
- コサイン波の値については、90度(π/2ラジアン)と270度(3π/2ラジアン)で0となる性質が、マクローリン変換においては「奇数の冪(べき)数が0になって消える」特徴として現れる。
統計言語Rによる作表例
target_names<-c("0 radian & 0 degree","π/2 radian & 90 degree","π radian & 180 degree","3/2π& 270 degree","2π & 360 degree")
target_values<-c("1","0","-1","0","1")
Circular_function<-data.frame(Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Circular_function), type = "html")Target_names Target_values 1 0 radian & 0 degree 1 2 π/2 radian & 90 degree 0 3 π radian & 180 degree -1 4 3/2π& 270 degree 0 5 2π & 360 degree 1 #統計言語Rによる検証例
plot(cos,xlim=c(-4,+4),ylim=c(-1,1),main="Cosine wave", xlab="X", ylab="Y")
- サイン波の値については、0度(0ラジアン)と270度(πラジアン)で0となる性質が、マクローリン変換においては「偶数の冪(べき)数が0になって消える」特徴として現れる。
#統計言語Rによる作表例
target_names<-c("0 radian & 0 degree","π/2 radian & 90 degree","π radian & 180 degree","3/2π& 270 degree","2π & 360 degree")
target_values<-c("0","1","0","-1","0")
Circular_function<-data.frame(Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Circular_function), type = "html")Target_names Target_values 1 0 radian & 0 degree 0 2 π/2 radian & 90 degree 1 3 π radian & 180 degree 0 4 3/2π& 270 degree -1 5 2π & 360 degree 0 #統計言語Rによる検証例
plot(sin,xlim=c(-4,+4),ylim=c(-1,1),main="Sine wave", xlab="X", ylab="Y")

- せっかくだからそれぞれの関数の値が1となるポイントが半径1の円を描く対数・指数関数と重ねたい。

- 「2乗すると-1になる複素数i」と「実数部をX軸に 、虚数部をY軸に割り当てる複素数平面(独Komplexe Zahlenebene, 英complex plane)の概念」を導入したら「位相が90度ズレた同じ波を直交させると円を描く」数理と上手く結び付けられた。
統計言語Rによる「オイラーの公式」の検証例
#まずは統計言語Rから呼べるYacasライブラリを導入
library(Ryacas)
#Cos(x)=x/1! - x^2/2! + x^4/4! - x^6/6! + x^8/8!...
yacas("Taylor(x, 0, 8) Cos(x)") #マクローリン展開
expression(1 - x^2/2 + x^4/24 - x^6/720 + x^8/40320)
#sin(x)=x/1! - x^3/3! + x^5/5! - x^7/7! + x^9/9!...
yacas("Taylor(x, 0, 11) Sin(x)") #マクローリン展開
expression(x - x^3/6 + x^5/120 - x^7/5040 + x^9/362880)
それぞれ自然対数eのマクローリン展開の一部っぽい。#Exp(x)=x/1! + x^2/2! + x^3/3! + x^4/4! + x^4/5! + x^6/6! + x^7/7! + x^8/8! + x^9/9!...
yacas("Taylor(x, 0, 9) Exp(x)") #マクローリン展開
expression(x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + x^6/720 + x^7/5040 +
x^8/40320 + x^9/362880 + 1)ただし、ただ合算しただけではCos関数とSin関数の合成関数を近似するのみである。
yacas("Taylor(x, 0, 9) Sin(x)+Cos(x)")
expression(x - x^2/2 - x^3/6 + x^4/24 + x^5/120 - x^6/720 - x^7/5040 +
x^8/40320 + x^9/362880 + 1)
ここに「2乗すると-1になる複素数i」の概念を導入すると符号違いの問題が解決されてExp(xi)=Cos(x)+Sin(xi)が成立するのです。
- Exp(xi)=xi/1!+xi^2/2!+xi^3/3!+xi^4/4!+xi^4/5!+xi^6/6!+xi^7/7!+xi^8/8!+xi^9/9!…
- Exp(xi)=1+xi-x^2/2-xi^3/3!+x^4/4!+xi^5/5!-x^6/6!-xi^7/7!+x^8/8!+xi^9/9!…
- Exp(xi)=(1-x^2/2+x^4/4-x^6/6!+x^8/8!…)+(xi-xi^3/3!+xi^5/5!-xi^7/7!+ xi^9/9!…)
- Exp(xi)=Cos(x)+Sin(xi)
まずはここまでの過程をグラフ化してみましょう。
ネイピア数を底(root)とする指数関数e^xのマクローリン展開
Macrolin_expansion_exp<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-6,6)
Graph_scale_y<-c(-1,6)
#関数と凡例の決定
switch(x,
"0"= f0<-function(x) {x/x},
"1"= f0<-function(x) {1+x},
"2"= f0<-function(x) {1+x+x^2/2},
"3"= f0<-function(x) {1+x+x^2/2+x^3/6},
"4"= f0<-function(x) {1+x+x^2/2+x^3/6+x^4/24},
"5"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120},
"6"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120+ x^6/720},
"7"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120+ x^6/720+ x^7/5040},
"8"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24+ x^5/120+ x^6/720+ x^7/5040+ x^8/40320},
"9"= f0<-function(x) {1 + x + x^2/2 + x^3/6+ x^4/24 + x^5/120 + x^6/720 + x^7/5040 + x^8/40320 + x^9/362880 }
)switch(x,
"0"=text<-c("1"),
"1"=text<-c("1+x"),
"2"=text<-c("1+x+x^2/2!"),
"3"=text<-c("1+x+x^2/2!+x^3/3!"),
"4"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!"),
"5"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!"),
"6"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!"),
"7"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!+x^7/7!"),
"8"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!+x^7/7!+x^8/8!"),
"9"=text<-c("1+x+x^2/2!+x^3/3!+x^4/4!+x^5/5!+x^6/6!+x^7/7!+x^8/8!+x^9/9!")
)f1=function(x){exp(x)}
plot(f1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="Macrolin expansion", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")legend("bottomleft", legend=c("e^x",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7","8","8","8","9","9","9")
saveGIF({
for (i in Time_Code){
Macrolin_expansion_exp(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
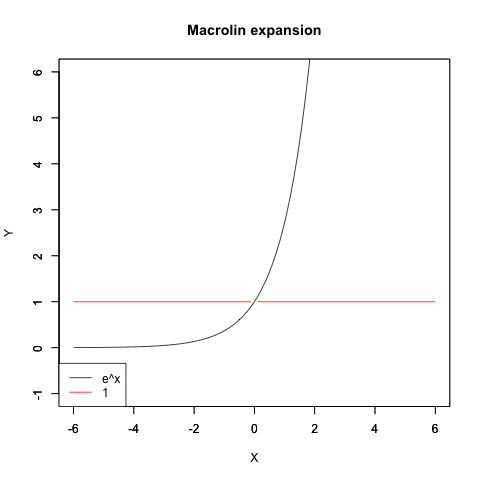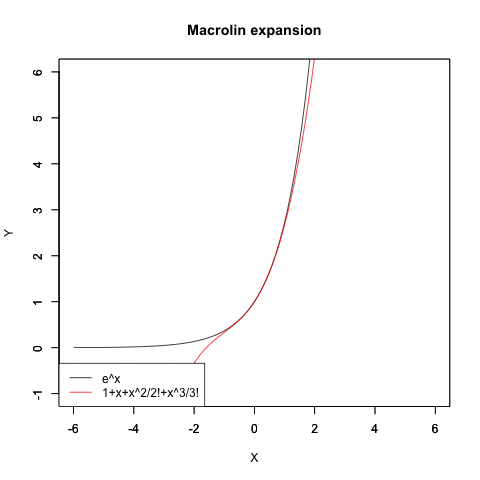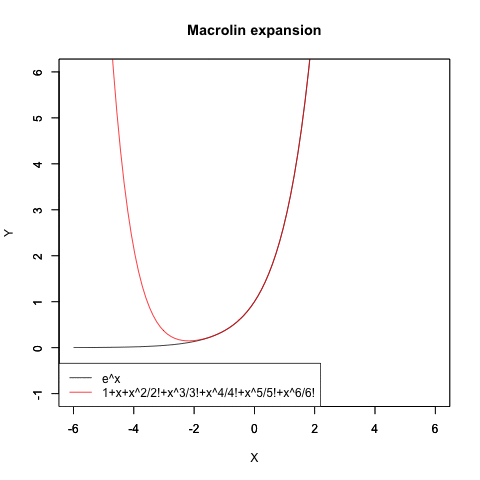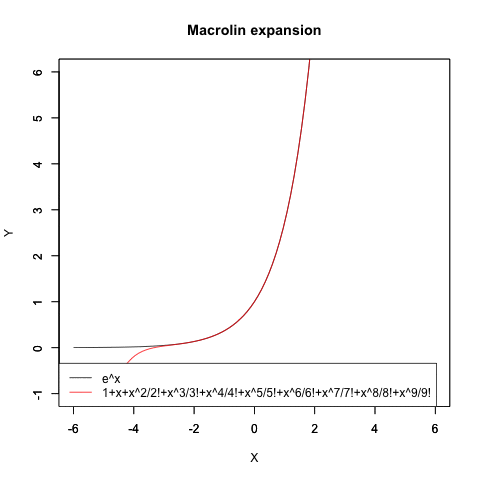
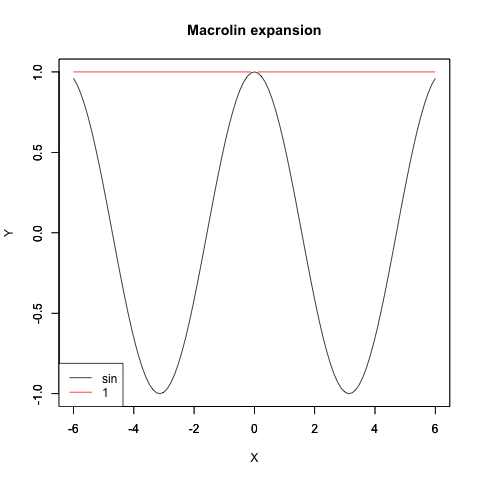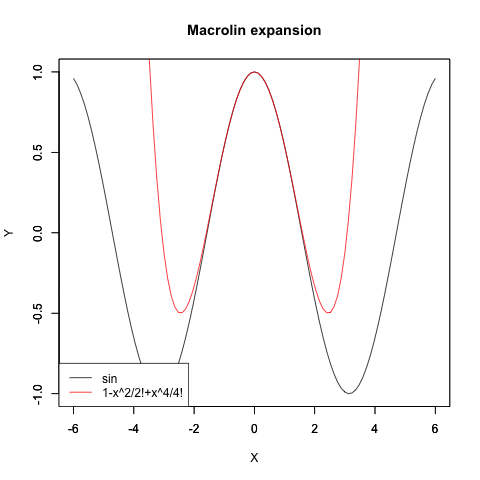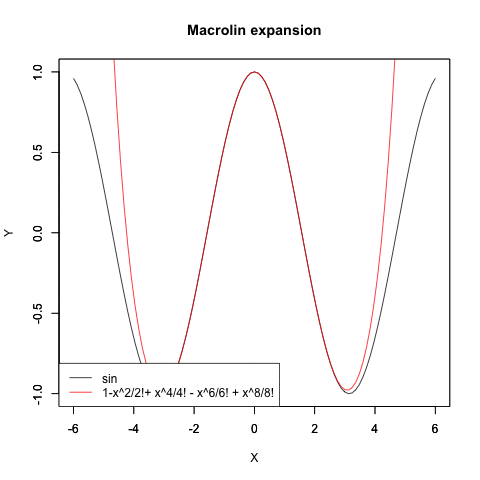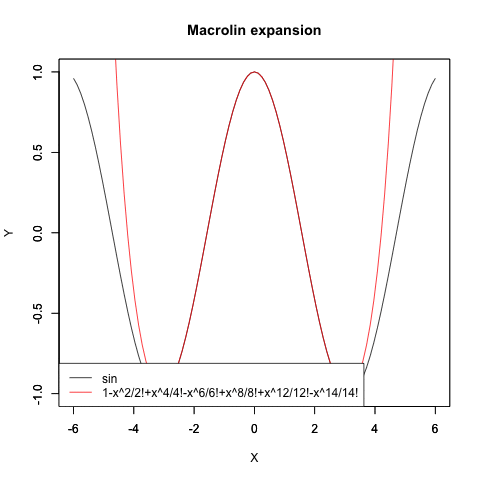
コサイン波のマクローリン展開
Macrolin_expansion_cos<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-6,6)
Graph_scale_y<-c(-1,1)
#関数と凡例の決定
switch(x,
"1"= f0<-function(x) {x/x},"2"= f0<-function(x) {1 - x^2/2},
"3"= f0<-function(x) {1 - x^2/2 + x^4/24},
"4"= f0<-function(x) {1 - x^2/2 + x^4/24 - x^6/720},
"5"= f0<-function(x) {1 - x^2/2 + x^4/24 - x^6/720 + x^8/40320},
"6"= f0<-function(x) {1 - x^2/2 + x^4/24 - x^6/720 + x^8/40320 +
x^12/479001600},
"7"= f0<-function(x) {1 - x^2/2 + x^4/24 - x^6/720 + x^8/40320 +
x^12/479001600 - x^14/87178291200}
)switch(x,
"1"=text<-c("1"),
"2"=text<-c("1-x^2/2!"),
"3"=text<-c("1-x^2/2!+x^4/4!"),
"4"=text<-c("1-x^2/2!+x^4/4!-x^6/6!"),
"5"=text<-c("1-x^2/2!+ x^4/4! - x^6/6! + x^8/8!"),
"6"=text<-c("1-x^2/2!+x^4/4!-x^6/6!+x^8/8!+x^12/12!"),
"7"=text<-c("1-x^2/2!+x^4/4!-x^6/6!+x^8/8!+x^12/12!-x^14/14!"),
)plot(cos,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="Macrolin expansion", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")legend("bottomleft", legend=c("sin",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7")
saveGIF({
for (i in Time_Code){
Macrolin_expansion_cos(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
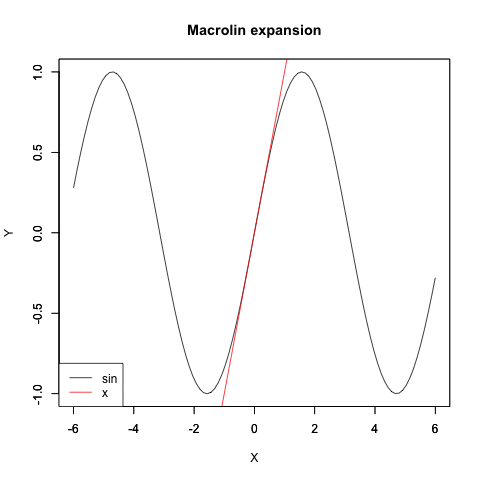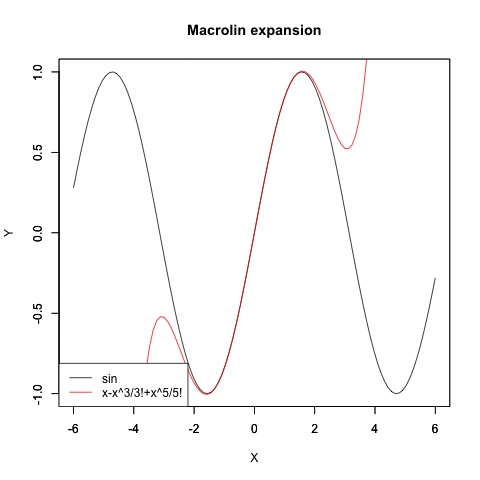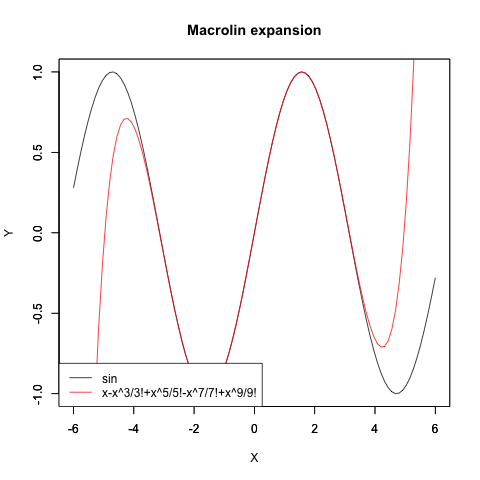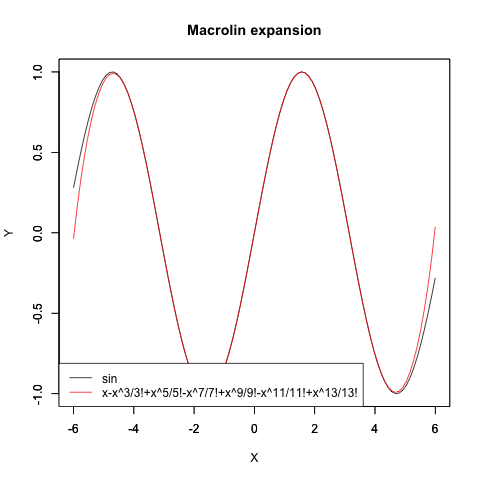
サイン波のマクローリン展開
Macrolin_expansion_sin<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-6,6)
Graph_scale_y<-c(-1,1)
#関数と凡例の決定
switch(x,
"1"= f0<-function(x) {x},"2"= f0<-function(x) {x - x^3/6},
"3"= f0<-function(x) {x - x^3/6 + x^5/120},
"4"= f0<-function(x) {x - x^3/6 + x^5/120 - x^7/5040},
"5"= f0<-function(x) {x - x^3/6 + x^5/120 - x^7/5040 + x^9/362880},
"6"= f0<-function(x) {x - x^3/6 + x^5/120 - x^7/5040 + x^9/362880 - x^11/39916800},
"7"= f0<-function(x) {x - x^3/6 + x^5/120 - x^7/5040 + x^9/362880 - x^11/39916800 +
x^13/6227020800}
)switch(x,
"1"=text<-c("x"),
"2"=text<-c("x-x^3/3!"),
"3"=text<-c("x-x^3/3!+x^5/5!"),
"4"=text<-c("x-x^3/3!+x^5/5!-x^7/7!"),
"5"=text<-c("x-x^3/3!+x^5/5!-x^7/7!+x^9/9!"),
"6"=text<-c("x-x^3/3!+x^5/5!-x^7/7!+x^9/9!-x^11/11!"),
"7"=text<-c("x-x^3/3!+x^5/5!-x^7/7!+x^9/9!-x^11/11!+x^13/13!")
)plot(sin,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="Macrolin expansion", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")legend("bottomleft", legend=c("sin",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7")
saveGIF({
for (i in Time_Code){
Macrolin_expansion_sin(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
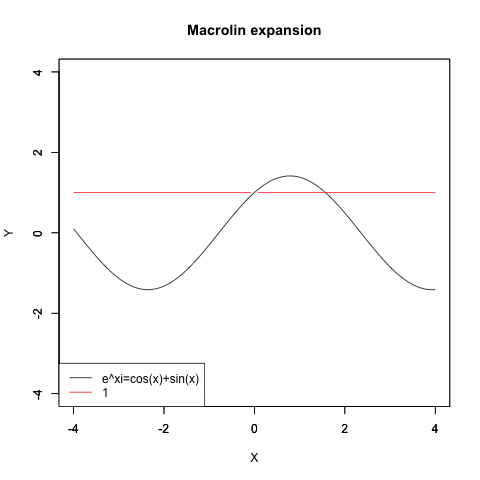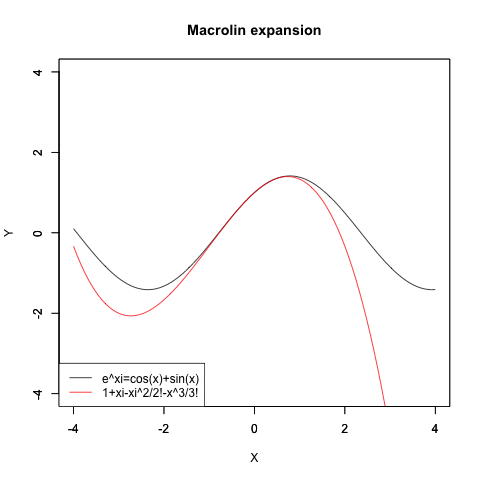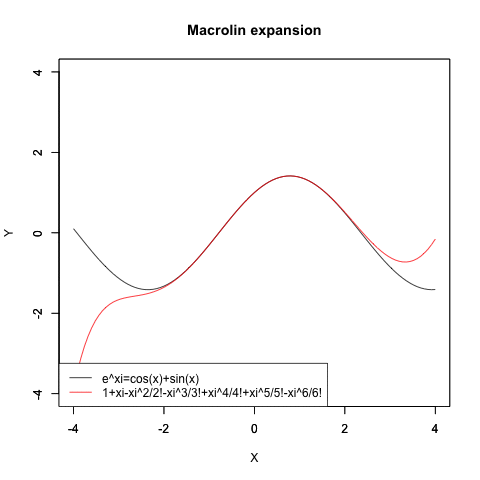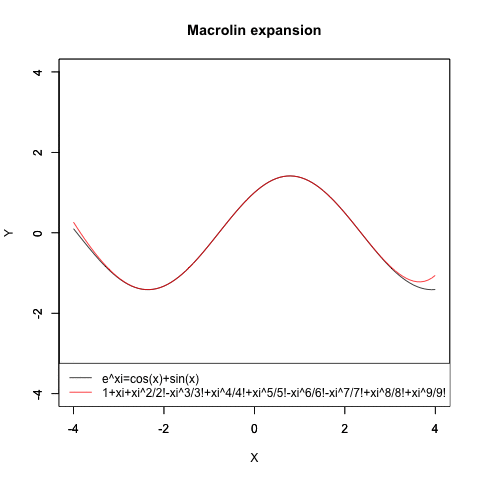
cos波とsin波の合成波の近似
Macrolin_expansion_circle<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-4,4)
Graph_scale_y<-c(-4,4)
#関数と凡例の決定
switch(x,
"0"= f0<-function(x) {x/x},
"1"= f0<-function(x) {1+x},
"2"= f0<-function(x) {1+x-x^2/2},
"3"= f0<-function(x) {1+x-x^2/2-x^3/6},
"4"= f0<-function(x) {1+x-x^2/2-x^3/6+x^4/24},
"5"= f0<-function(x) {1+x-x^2/2-x^3/6+x^4/24+x^5/120},
"6"= f0<-function(x) {1+x-x^2/2-x^3/6+x^4/24+x^5/120-x^6/720},
"7"= f0<-function(x) {1+x-x^2/2-x^3/6+x^4/24+ x^5/120-x^6/720- x^7/5040},
"8"= f0<-function(x) {1+x-x^2/2-x^3/6+x^4/24+x^5/120-x^6/720+ x^7/5040+ x^8/40320},
"9"= f0<-function(x) {1+x-x^2/2-x^3/6+x^4/24+x^5/120-x^6/720- x^7/5040+x^8/40320+x^9/362880 }
)switch(x,
"0"=text<-c("1"),
"1"=text<-c("1+xi"),
"2"=text<-c("1+xi-xi^2/2!"),
"3"=text<-c("1+xi-xi^2/2!-x^3/3!"),
"4"=text<-c("1+xi-xi^2/2!-xi^3/3!+x^4/4!"),
"5"=text<-c("1+xi-xi^2/2!-xi^3/3!+x^4/4!+x^5/5!"),
"6"=text<-c("1+xi-xi^2/2!-xi^3/3!+xi^4/4!+xi^5/5!-xi^6/6!"),
"7"=text<-c("1+xi-xi^2/2!-xi^3/3!+xi^4/4!+xi^5/5!-xi^6/6!-xi^7/7!"),
"8"=text<-c("1+xi-xi^2/2!-xi^3/3!+xi^4/4!+xi^5/5!-xi^6/6!-xi^7/7!+xi^8/8!"),
"9"=text<-c("1+xi+xi^2/2!-xi^3/3!+xi^4/4!+xi^5/5!-xi^6/6!-xi^7/7!+xi^8/8!+xi^9/9!")
)
f1<-function(x){cos(x)+sin(x)}
plot(f1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="Macrolin expansion", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")legend("bottomleft", legend=c("e^xi=cos(x)+sin(x)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7","8","8","8","9","9","9")
saveGIF({
for (i in Time_Code){
Macrolin_expansion_circle(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
虚数概念導入による指数関数e^xi=cos(x)+sin(xi)の公式の成立
Macrolin_expansion_circle<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-4,4)
Graph_scale_y<-c(-4,4)
#関数と凡例の決定
switch(x,
"0"= f0<-function(x) {x/x},
"1"= f0<-function(x) {1+x*(0+1i)},
"2"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2},
"3"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6},
"4"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24},
"5"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120},
"6"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120+(x*(0+1i))^6/720},
"7"= f0<-function(x) {1+x*(0+1i)-(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120+(x*(0+1i))^6/720+(x*(0+1i))^7/5040},
"8"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120+(x*(0+1i))^6/720+(x*(0+1i))^7/5040+(x*(0+1i))^8/40320},
"9"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24 +(x*(0+1i))^5/120+(x*(0+1i))^6/720+(x*(0+1i))^7/5040 +(x*(0+1i))^8/40320 + x^9/362880 }
)switch(x,
"0"=text<-c("1"),
"1"=text<-c("1+xi"),
"2"=text<-c("1+xi+xi^2/2!"),
"3"=text<-c("1+xi+xi^2/2!+x^3/3!"),
"4"=text<-c("1+xi+xi^2/2!+xi^3/3!+x^4/4!"),
"5"=text<-c("1+xi+xi^2/2!+xi^3/3!+x^4/4!+x^5/5!"),
"6"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!"),
"7"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!+xi^7/7!"),
"8"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!+xi^7/7!+xi^8/8!"),
"9"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!+xi^7/7!+xi^8/8!+xi^9/9!")
)
f1<-function(x){cos(x)+sin(x*(0+1i))}
plot(f1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="Macrolin expansion", xlab="X", ylab="Y")
par(new=T)#上書き指定
plot(f0,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")legend("bottomleft", legend=c("e^xi=cos(x)+sin(xi)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7","8","8","8","9","9","9")
saveGIF({
for (i in Time_Code){
Macrolin_expansion_circle(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")

これだけではまだ円を描きません。それにはさらに「実数部をX軸に 、虚数部をY軸に割り当てる複素数平面(独Komplexe Zahlenebene, 英complex plane)の概念」の導入が必要とされたのでした。
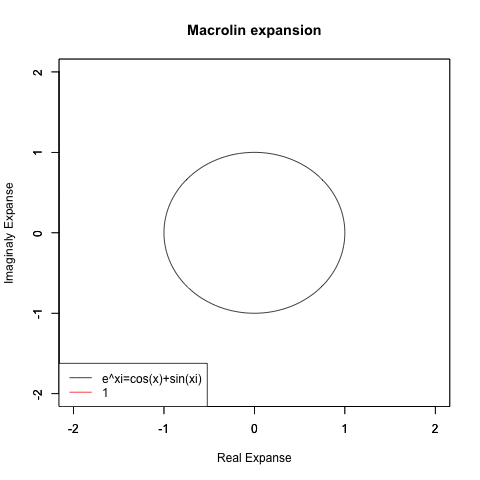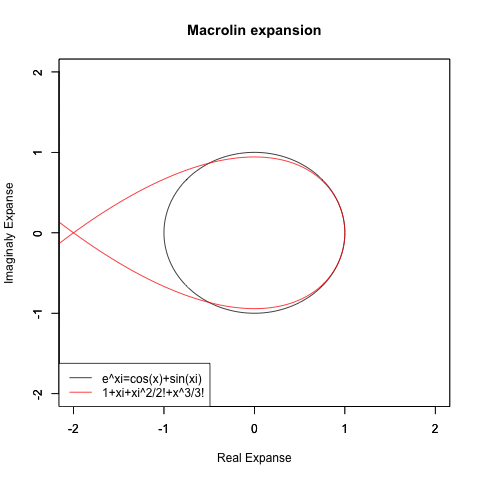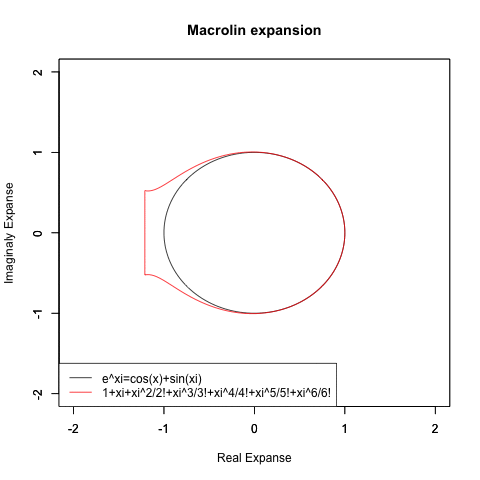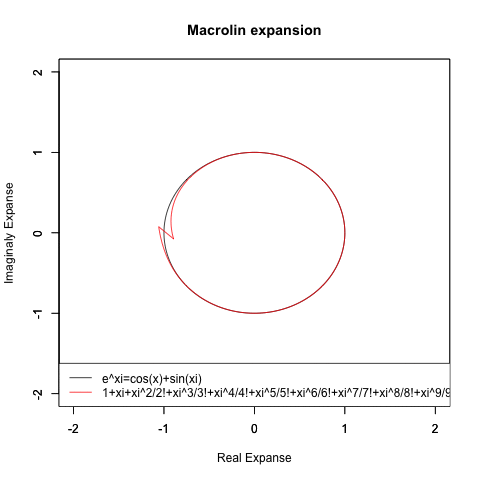
虚数概念の導入による指数関数e^xi=cos(x)+sin(xi)の公式の成立
Macrolin_expansion_circle<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-2,2)
Graph_scale_y<-c(-2,2)
#関数と凡例の決定
switch(x,
"0"= f0<-function(x) {x/x},
"1"= f0<-function(x) {1+x*(0+1i)},
"2"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2},
"3"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6},
"4"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24},
"5"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120},
"6"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120+(x*(0+1i))^6/720},
"7"= f0<-function(x) {1+x*(0+1i)-(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120+(x*(0+1i))^6/720+(x*(0+1i))^7/5040},
"8"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24+(x*(0+1i))^5/120+(x*(0+1i))^6/720+(x*(0+1i))^7/5040+(x*(0+1i))^8/40320},
"9"= f0<-function(x) {1+x*(0+1i)+(x*(0+1i))^2/2+(x*(0+1i))^3/6+(x*(0+1i))^4/24 +(x*(0+1i))^5/120+(x*(0+1i))^6/720+(x*(0+1i))^7/5040 +(x*(0+1i))^8/40320 + x^9/362880 }
)switch(x,
"0"=text<-c("1"),
"1"=text<-c("1+xi"),
"2"=text<-c("1+xi+xi^2/2!"),
"3"=text<-c("1+xi+xi^2/2!+x^3/3!"),
"4"=text<-c("1+xi+xi^2/2!+xi^3/3!+x^4/4!"),
"5"=text<-c("1+xi+xi^2/2!+xi^3/3!+x^4/4!+x^5/5!"),
"6"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!"),
"7"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!+xi^7/7!"),
"8"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!+xi^7/7!+xi^8/8!"),
"9"=text<-c("1+xi+xi^2/2!+xi^3/3!+xi^4/4!+xi^5/5!+xi^6/6!+xi^7/7!+xi^8/8!+xi^9/9!")
)theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
plot(cos(theta), sin(theta),xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0),main="Macrolin expansion", xlab="Real Expanse", ylab="Imaginaly Expanse")
par(new=T)#上書き指定Re01=Re(f0(theta))
Im01=Im(f0(theta))
plot(Re01,Im01,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(1,0,0),main="", xlab="", ylab="")legend("bottomleft", legend=c("e^xi=cos(x)+sin(xi)",text),lty=c(1,1),col=c(rgb(0,0,0),rgb(1,0,0)))
}
library("animation")
Time_Code=c("0","0","0","1","1","1","2","2","2","3","3","3","4","4","4","5","5","5","6","6","6","7","7","7","8","8","8","9","9","9")
saveGIF({
for (i in Time_Code){
Macrolin_expansion_circle(i)
}
}, interval = 0.1, movie.name = "TEST01.gif")
複素数平面(独Komplexe Zahlenebene, 英complex plane) - Wikipedia
1811年頃にガウス(Johann Carl Friedrich Gauß、1777年〜1855年)によって導入されたため、ガウス平面 (Gaussian plane) とも呼ばれる。一方、それに先立つ1806年にJean-Robert Argandも同様の手法を用いたため、アルガン図 (Argand Diagram)とも呼ばれている。さらに、それ以前の1797年のCaspar Wesselの書簡にも登場している。このように複素数の幾何的表示はガウス以前にも知られていたが、今日用いられているような形式で複素平面を論じたのはガウスである。三者の名前をとってガウス・アルガン平面、ガウス・ウェッセル平面などとも言われる。
あれ、オイラーの等式e^πi=-1が先に成立した訳ではない?
Mathematics and Its Historyによると、 1702年にオイラーの師匠であるヨハン・ベルヌーイが1/(1+z^2)=(1/2)*(1/(1+Zi)+1/(1/(1-Zi)))という部分分数分解において、左辺の積分は tan−1、右辺の積分は ( i が虚数であることを忘れれば) log になるはずなので、複素数の対数にも何らかの意味がありそうだということに気づいたそうです。
しかし対数関数ではどうも上手く行かず、1740年にオイラーがその逆関数である指数関数で「オイラーの公式」を見つけ、1748年に例のゴリゴリの方法での証明を発表した、ということのようです。
ネイピア数eが無理数である(テイラー展開の結果が0に収束しない)事が証明されたのは1744年である(ネイピア数の無理性の証明、オイラー)。
e が無理数であることの証明は円周率πが無理数であることの証明よりずっと易しい。π の無理性が初めて示されたのは1761年のことである。
言われてみれば、確かに騒がれ出したのは主に19世紀に入ってから…
オイラーの等式(Euler's identity) - Wikipedia
数学誌のThe Mathematical Intelligencerの読者調査によると、この等式は「数学における最も美しい定理 (The most beautiful theorem in mathematics) 」に選出されている。また、2004年に実施された Physics World 誌での読者調査ではマクスウェルの方程式と並び、「史上最も偉大な等式(Greatest equation ever) 」に選出されている。
ポール・ネイヒン(ニューハンプシャー大学名誉教授)の著書「オイラー博士の偉大な式(Dr. Euler's Fabulous Formula、2006)」では、この等式のために400ページも充てている。本著書ではこの等式を「数学的な美の絶対的基準(The gold standard for mathematical beauty) 」としている。コンスタンス・レイドは、オイラーの等式を「全ての数学分野において最も有名な式(The most famous formula in all mathematics) 」であると主張した。
カール・フリードリッヒ・ガウスは「この式を見せられた学生がすぐにその意味を理解できなければ、その学生は第一級の数学者には決してなれない(If this formula was not immediately apparent to a student on being told it, the student would never be a first-class mathematician.) 」と指摘している。
この等式がベンジャミン・パース (19世紀の数学者、ハーバード大学教授) の講義で紹介されたあと、「全く逆説的なことだ、我々はそれを理解できないし、それがどんな意義を持っているかも分からない。だが我々はそれを証明したし、それゆえにそれが間違いのない真実であると知っている(It is absolutely paradoxical; we cannot understand it, and we don't know what it means, but we have proved it, and therefore we know it must be the truth.) 」と付け加えた。
スタンフォード大学の数学の教授、キース・デブリンは「愛の本質そのものをとらえるシェークスピアのソネットのように、あるいは、単なる表面でなくはるかに深い内面から人間の形の美しさを引き出す絵画のように、オイラーの等式は存在の遥かな深遠にまで到達している(Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler's equation reaches down into the very depths of existence.) 」と記している。
Bob Palaisが2001年に公開したエッセイ "π is wrong!" の中では、円周率πの代わりに、τ、円の周の半径に対する比率を用いれば、この式はe^τ= 1という、よりシンプルな表現になると述べられている。
