貴方は「数学上の自然概念(Nature of Mathematics)」について、どれだけ有識か?
How much do you know about "The Nature of Mathematics"?

そもそも最近、数の概念は自然数(Natural Number)N=1,2,3,…∞から出発し整数(Integer)Z=-∞…-1,-2,-3,0,1,2,3,…∞を経て有限少数(Finite decimal)や循環小数(Circulating decimal)で構成される分数(Fraction)を加えた有理数(Rational Number:直訳すると「割り切れる数」)Qや「割り切れない」が数直線上には置ける無理数(Irrational number)を加えた実数(Real number)R、これに虚数(imaginary number)を加えた複素数(Complex number)Cへと拡充されてきたとする仮説自体に納得が行かなくなってきたのです。
何よりもまず「コンピューター上の数概念(Number concept on computer)」自体がこうした前提にそれほど敬意を払っていない様に見えるのです。そしてさらに、それはそれでそれなりに上手くいってる様に見えます。これはどういう事でしょう?
- とにかく生物の世界認識方法の根幹は(上掲の基準には一切登場しない)対数尺に依存してきたといえる。
- ところがカンブリア爆発期(約5億4200万年前〜約4億8830万年前)に入ると「目と視覚情報を処理する中枢神経」を備えた左右相称動物(Bilateria、カニやエビの様な節足動物の先祖筋)が、動きの鈍重な放射相称動物(Radiata、ウニやクラゲやイソギンチャクの類)を圧倒する様になり、前者はある種の仮想世界(Virtual Reality)すなわち「オイラーの原始量(Euler's primitive sweep)=観測原点をすっぽり包む全球型スクリーン」の世界で生きる様になる。
まずはあらゆる空間的概念の原風景として「オイラーの原始量(Euler's primitive sweep)=観測原点をすっぽり包む全球型スクリーン」なる概念を仮定する。

①任意の観測原点「0」を設置する。この時点ではまだ何も起こってはいない。

- この段階で既に「観測原点をすっぽり包む全球型スクリーン」は実在しているが上映前の映画館のスクリーンの様に何も投影されてない。この状態を幾何学上の1角形(頂点や辺や面の概念が全て1点上に集約する図形。球表面上においてのみ認識可能)に対応させる向きもある。
*この時点で既に「回転の向き」なる概念も存在するが、それに特別な意味を持たせる事は出来ない。
- ここで急浮上してくるのが「有意味なデータの抽出(Extract Significantly result of the data obsertion)」が「無視可能なデータの切り捨て(Reject Ignorableresult of the data obsertion)」と表裏一体の関係にある問題。すなわちシステムの出力がゼロなのは入力がゼロだからとは限らない。「分析可能な情報」がまだ一つも得られてない段階だからに過ぎないかもしれないという話。
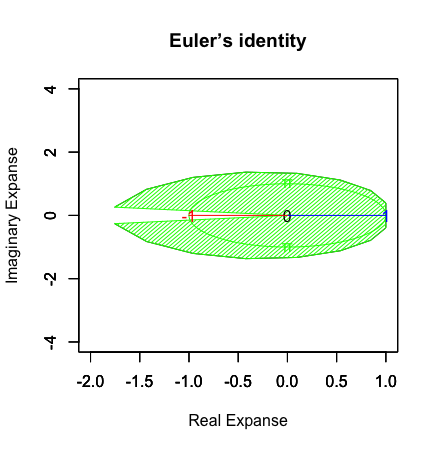
②何かが観測されると、たちまち観測原点「0」と対象「1」とを結ぶ距離1の線分(比較対象がないので、とりあえずそう認識するしかない。実際にはスカラー(定数)でなく状況に応じて伸縮するのかもしれないが、その判断にも相応の情報量を必要とする)の旋回範囲に(これを半径とする)円周/円や球面/球が現出し「観測原点をすっぽり包む全球型スクリーン」がやっと意味を持ち始める。「直径2」の概念が芽生える瞬間でもあり、その極限値は観測原点より半径分「1」あるいは半周分「π」離れた先に極限値「−1」。複素系座標操作でいうところのオイラーの等式(Euler's identity)1+πi=-1+0iの世界。

- これを球形幾何学における二角形(digon)に対応させる向きもある。
正2角形(pi/2=3.141593ラジアンあるいは180度)の場合…概ね「任意の円弧を2分割する2点(直線距離1に対して円弧上の距離はπ/2倍)、あるいは出発地点と到着定点の間を等しい測地線で結ぶ球表面上の円弧を観測原点とその面幾何学においておける原点出発点と終点を等しくする円周もしくは球上の一点」を指す。例えば任意の球表面上において出発点「1」とその座標上正反対に位置する対蹠地「−1」の間を(両者の直線距離1に対してπ/2倍の距離で結ぶ)無数の測地線など。
③このイメージは人類の想像力を微積分の様な解析学分野や量子力学の世界に誘った数学的直感の大源流でもあったと考えられている。

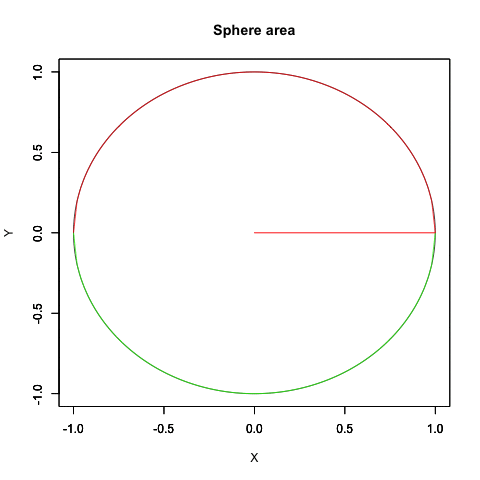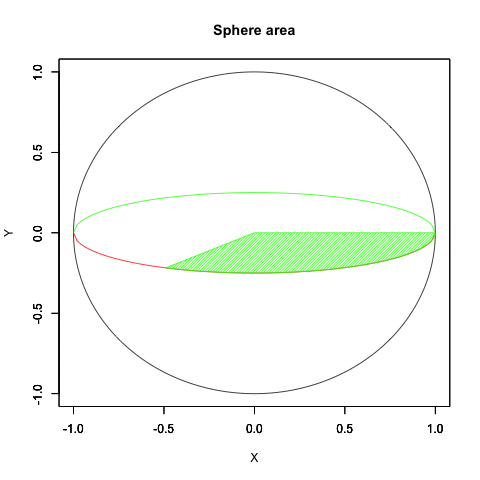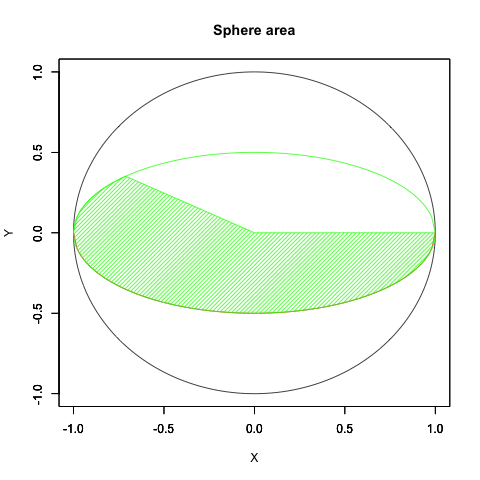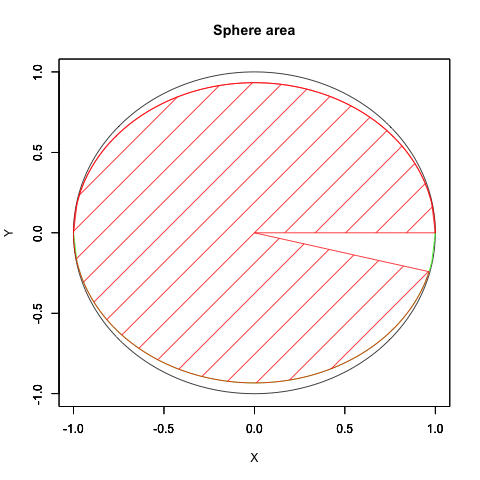
ある意味、これこそが「極座標系(polar coordinates system)」概念の大源流?
- この段階で既に「観測原点をすっぽり包む全球型スクリーン」は実在しているが上映前の映画館のスクリーンの様に何も投影されてない。この状態を幾何学上の1角形(頂点や辺や面の概念が全て1点上に集約する図形。球表面上においてのみ認識可能)に対応させる向きもある。
-
現れた当初、それは多様な生存戦略の一貫に過ぎなかったが、やがてある意味、当事者の世界認識能力そのものへと変貌していく。
その過程で片対数尺(Semi-logarithmic scale)を発展させる形で等差数列(Arithmetic sequence)で目盛りが振られたN個の座標軸(Coordinate axes)が直交(Orthogonal)する「デカルト座標系(Cartesian coordinate system)」を巡る諸概念が(極座標系概念との変換方法も含め)整備されてきた?
統計言語Rによる3D表示(z軸=t)library(rgl)
ccs_x<-seq(-3*pi,3*pi,length=180)
ccs_y<-ccs_x
ccs_z<-ccs_x
plot3d(ccs_x,ccs_y,ccs_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")

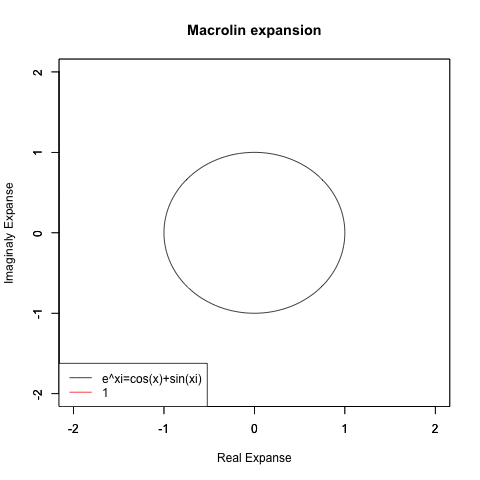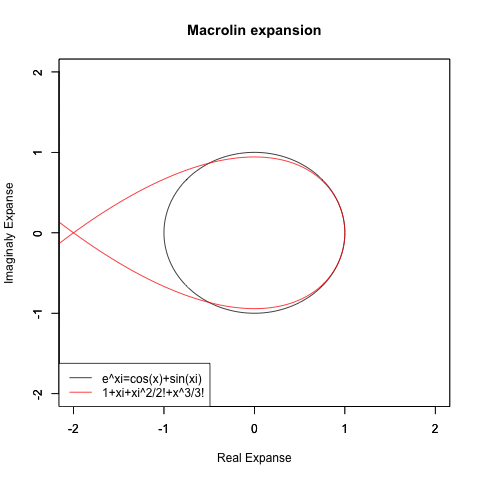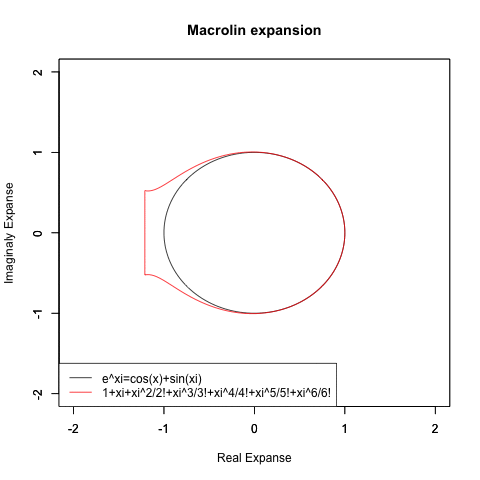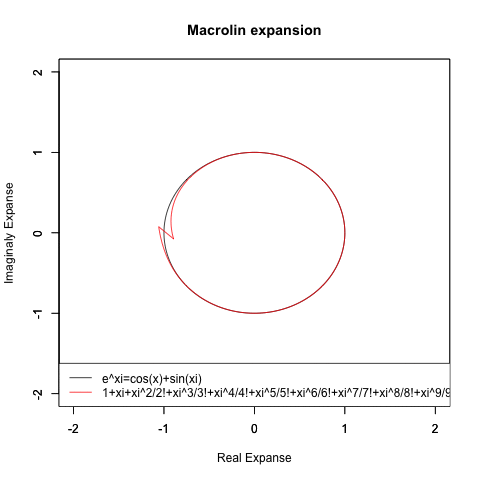
- そして直交座標系(Arthogonal coordinate system)や極座標系(Polar coordinates system)は、等差数列(Arithmetic sequence)や等比数列(Geometric sequence)を目盛りとする数直線的展開や「奇関数と偶関数の振る舞いの違い」などを扱う関数のベクトル表現といった諸概念を共有する。というより、両者の統合要求こそがテイラー級数(Taylor series)/マクローリン級数(McLoughlin series)、そしてフーリエ解析(
Fourier analysis)などを「自然に(Naturally)」生み出してきたというのが正しいとも解釈可能である。


こうした全体像をそれなりに掌握してやっと「人類の数学史(History of human mathematics)」の全体像について語る準備が整った訳です。
①そもそも人類はその大半が長い期間、加減算と実用に欠かせない特殊な乗除算の知識飲みに頼って生活してきた。例外は農暦をメンテナンスしたり、建築や航海によって生活する一部技術者のみで、彼らがその方面における社会全体に対する発言権を有する機会は決して存在しなかった。
中世ヨーロッパ初期の騎士たちの世界では、文字が読めるような奴は軟弱者扱いときいて、当時の騎士たちの男としての純度の高さに驚愕した。あの男塾ですら知性や教養へのリスペクトは一応あったんやぞ… pic.twitter.com/CsUVwIQDSw
— 坂之上田村フレンズ (@pokitasu) August 29, 2019
②最初のパラダイムシフト(Paradigm shift)は欧州で起こった。
大航海時代(The voyage era、15世紀中旬〜17世紀中旬)到来に伴い、この地域の経済的中心が地中海沿岸部から大西洋沿岸部に推移し、それまで文化の中心だった地中海沿岸部が(大西洋沿岸部への食糧輸出が最大の代替収入源だった事から)「領主が領土と領民を全人格的に代表する農本主義的権威体制」に後退。その一方で「必要にして十分な火力と機動力(当時の概念としては陸路における道路や中継駅の整備力や、水路における戦闘への投入可能な船舶保有量を指した)を備えた常備軍を中央集権的官僚体制が徴税によって養う体制」を前提とする主権国家(羅Civitas Sui Iuris)/法人(独Juristische Person、仏Personne morale、英Juridical person)概念導入に不可欠な複式簿記の知識のヴェネツィアからの流出と、当時の出版革命が新たな時代の呼び水となったのである。
貨幣に記された記号が文字の誕生のきっかけとなったとする説、面白いな(こなみ
— ガリポリ (@christianharuhi) August 29, 2019
奇しくも「虚数(Imaginary number)」概念の起源もまたルネサンス期のイタリアまで遡る。それまで数学分野の発展が地中海文化圏でも最低だった状況からの脱却開始…
(航海や測量に欠かせない)円周率や三角関数の数表の制度追求要求が17世紀に対数関数を、18世紀に指数関数を発見させた。人類の数学史ではこの時代が一つのパラダイムシフトとなっている。
a=0の時
- ① a^0 = 1
統計言語Rによる計算例
*a=1の場合の結果は全て1となる。3^0
[1] 12^0
[1] 11^0
[1] 1a ≠ 0で、nが正の数の時
- ② a^-n = 1/a^n
統計言語Rによる計算例(計算機代数ソフトウェアYacas使用)
library(Ryacas)
#1の段
yacas("1^-1") #1/1^1
expression(1)
yacas("1^-2") #1/1^2
expression(1)
yacas("1^-3") #1/1^3
expression(1)
#2の段
yacas("2^-1") #1/2^1
expression(1/2)
yacas("2^-2") #1/2^2
expression(1/4)
yacas("2^-3") #1/2^3
expression(1/8)
#3の段
yacas("3^-1") #1/3^1
expression(1/3)
yacas("3^-2") #1/3^2
expression(1/9)
yacas("3^-3") #1/3^3
expression(1/27)*a=1の場合の結果は全て1となる。
a ≠ 0で、m、nが正の数の時
- ③ a^m*a^n = a^(m+n)
統計言語Rによる計算例
2^3*2^4
[1] 128
2^(3+4)
[1] 128*この性質を利用して乗算を加算に単純化可能。
- ④ (a^m)^n = a^(m*n)
統計言語Rによる計算例
(2^3)^4
[1] 4096
2^(3*4)
[1] 4096*この性質を利用して累乗算を乗算に単純化可能。
- ⑤ a^m/a^n = a^(m-n)
統計言語Rによる計算例(計算機代数ソフトウェアYacas使用)
library(Ryacas)
#計算結果
yacas("2^3/2^4")
expression(1/2)
yacas("2^(3-4)")
expression(1/2)*この性質を利用して除算を減算に単純化可能。
a ≠ 0、b ≠ 0で、m、nが整数の時
- ⑥ (a*b)^n = a^n*b^n
統計言語Rによる計算例
(2*3)^4
[1] 1296
2^4*3^4
[1] 1296*実はここに列記した「指数関数7大法則」の中では、次に述べる「(a/b)^n = a^n/b^n」法則同様にあまり使われない。理由は後述。
- ⑦ (a/b)^n = a^n/b^n
統計言語Rによる計算例(計算機代数ソフトウェアYacas使用)
library(Ryacas)
#計算結果
yacas(" (2/3)^4")
expression(16/81)
yacas("2^4/3^4")
expression(16/81)*わざわざYacasを使ったのは、この計算があくまで「有理数(Rational number)」すなわち「分数(Fraction)で表せる範囲」に留まっている事を示すため。
ところで、指数関数y=a^xをx=a^yに変形すると対数関数y=log(x,base=a)となり、当然上掲の指数法則がそのまま逆対応する。
- ① log(1,base=a) = 0(ただしa が1でない正の数のとき)
統計言語Rによる計算例
log(1,base=1)
[1] NaN
警告メッセージ:
計算結果が NaN になりました
log(1,base=2)
[1] 0
log(2,base=2)
[1] 1
log(1,base=3)
[1] 0
log(3,base=3)
[1] 1*指数関数で「底(base,root)」が0になってはいけない様に、対数関数ではそれが1になってはならない。なお、Log関数はbase=指数の時に1を返す。
② log(-n,base=a) = 1/log(n,base=a) (ただしmnが正の数,a が1でない正の数の時)
統計言語Rによる計算例
log(1/2,base=2)
[1] -1
1/log(1/2,base=2)
[1] -1*後述する理由により、こういう時計算機代数ソフトウェアYacasは役に立たないのである。
- ③log(m^n,base=a) = n*log(m,base=a)(x・yが正の数,a が1でない正の数のとき)
統計言語Rによる計算例
log(3^4,base=2)
[1] 6.33985
4*log(3,base=2)
[1] 6.33985*ここでは乗算が指数上の類乗算に置換される。
④log(m*n,base=a) = log(m,base=a)+log(n,base=a)
統計言語Rによる計算例log(3*4,base=2)
[1] 3.584963
log(3,base=2)+log(4,base=2)
[1] 3.584963*ここでは加算が指数上の乗算に置換される。
⑤ log(b,base=a)-log(c,base=a)=log(b/c,base=a)
統計言語Rによる計算例
log(3/4,base=2)
[1] -0.4150375
log(3,base=2)-log(4,base=2)
[1] -0.4150375*ここでは減算が指数上の除算に置換される。
- ⑥log(a,base=b) = log(b,base=c)/log(a,base=c)
統計言語Rによる計算例
log(2,base=3)
[1] 0.6309298
log(2,base=4)/log(3,base=4)
[1] 0.6309298*しばしば「根(base,root)の変換式」と呼ばれる。
その一方で指数関数(The exponential function)や対数関数(Logarithmic function)における指数(Index)の分数表現や少数表現は平方根(The square root)や立方根(The cube root)概念、ひいては正多角形(Regular polygon)と内接円(Inscribed circle)/外接円(Circumscribed circle)の追求を経て「円周率Pi(3.141593…)」の近似問題に至る。そう「目盛り設定(Scale setting)」や「正規化(Normalization:合計値または積分値を1にする)」作業の本質もまさに「周期関数(Periodic function)」の設定基準に準拠するのである。
何しろ「指数・対数関数の発見」は、人類にとって円周率や平方根/立方根、そして三角関数に次ぐ無理数ネイピア数e(2.718282)および1/e(0.3678794)との邂逅をもたらしたのである。
①「大数の弱法則 (WLLN: Weak Law of Large Numbers) 」の提唱者たるヤコブ・ベルヌーイ(Jakob Bernoulli、1654年〜1705年)とその弟子レオンハルト・オイラー(Leonhard Euler, 1707年〜1783年)は、「各出目の出現確率が均等に1/6の六面体サイコロを6回降って特定の目が1回も出ない確率」なる概念を数式的に抽象化した(1-1/N)^Nの式を通じてネイピア数1/e=0.3678794の概念に到達した。
- 大数の弱法則 (WLLN: Weak Law of Large Numbers) …独立同分布/独立同一分布に従う可積分な確率変数の無限列X1, X2,…Xnとその平均μが与えられた時、標本平均(Sample mean)(X1, X2,…Xn)/n(ただしn>=1) のとる値が平均μの近傍から外れる確率は、十分大きなnを取れば、いくらでも小さくできるとする考え方。
- 独立同分布/独立同一分布(independent and identically distributed; IID, i.i.d., iid)…確率論と統計学において、確率変数の列やその他の系が、それぞれの確率変数が他の確率変数と同じ確率分布を持ち、かつ、それぞれ互いに独立している場合をいう。例えば6面体サイコロで各出目の確率は毎回1/6であり、その前後の出目の影響を受けない(メモリレス性)。「独立同分布/独立同一分布」なる確率分布自体が存在する訳ではない点に注意。
可積分(integrable)…ニュートンが17世紀にケプラー問題を解いて微分積分学や古典力学が発祥して以降追求されてきた「求積法で完全に解ける」範囲。
例えば「物差しの目盛は収束などしてはいけない」ルールに従って指数・対数関数や三角関数を「収束しない基準」として採用したフーリエ解析(Fourier analysis)におけるフーリエ展開(Fourier expansion)/フーリエ逆展開(Fourier inverse expansion)は、その立ち場故に指数・対数関数や三角関数そのものを直接扱えない(決して収束しないからこそ正負の目盛りが無限に続き微積分演算の対象となり得ない)。あえてこの制約を破ろうとしたのがラプラス変換となる。
- 確率変数(random variable, aleatory variable, stochastic variable)…ある確率のセットが変数として存在し、しかも概ねそうした確率の合計が1となる様に正規化(normalization)された状態モデルを指す。例えばコインの出目は{表,裏}のいずれかで、それぞれの目が出る確率は1/2(P(X)=1/2(x=0,1))。6面体サイコロを投げて出る目は{1, 2, 3, 4, 5, 6}のいずれかで、それぞれの目が出る確率は1/6(P(X)=1/6(x=1,2,3,4,5,6))。3の目が出る確率は1/6(P(X=3)=1/6,P(3)=1/6)。
一般化するとP(X)=1/N(X=1,2,3…N)となり、ここから先に述べた(1-1/N)^N(各出目の出現確率が均等に1/NのN面体サイコロをN回降って特定の目が1回も出ない確率)なる式も導出されたのである。
②さらにベルヌーイとオイラーは「一年で元金が倍になる夢の金融商品において、複利計算でさらに利益を上げられる上限」なる概念を数式的に抽象化した(1+1/N)^Nの式の究極解としてネイピア数e=2.718282そのものにも到達。
③両者が逆数関係にあった事から既存の対数関数論を敷衍する形で自然指数関数(Natural exponential function)y=e^xと自然対数関数(Natural logarithm function)x=e^yあるいはy=log(x)を発案した。
④ところで等速円運動をそれぞれX軸とY軸より観測すると2つの単振動(位相が90度ズレたCos波とSin波)が得られ、それを再構成する形で円が描ける。
⑤同様に(奇関数と偶関数が無限に連続する)自然指数・対数関数と(偶関数を実数に、奇関数を虚数に割り当てる)虚数指数(Imaginary exponent)と(実数をX軸に割り振り、虚数をY軸に割り振る)複素平面(独Komplexe Zahlenebene, 英complex plane)を組み合わせても単位円(半径1の円弧)が現れる。有名なオイラーの公式e^θi=cos(θ)+sin(θi)とはこれ。
統計言語Rによる3D表示
library(rgl)
#complex_plane_z=時間軸t
complex_plane_z<-seq(-3*pi,3*pi,length=180)
#complex_plane_x=実数軸(Real number)
complex_plane_x<-cos(complex_plane_z)
#complex_plane_y=虚数軸(Imaginary number)
complex_plane_y<-sin(complex_plane_z)
#グラフ描写
plot3d(complex_plane_x,complex_plane_y,complex_plane_z)
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test")
以降、指数関数と対数関数はまとめてネイピア数eを底(root,base)とする指数関数e^xと指数関数log(x,base=e)を中心に考えられるようになった。この時、底のズレは以下の式で修正される。
- 指数関数の場合はy=e^(log(底(root))*x)
- 対数関数の場合はx=e^(log(底(root))*y)すなわちy=log(x)/log(底(root))。

③こうした測定精度の急激な上昇具合が、人類の地理感覚の「周囲を巨大海棲生物が徘徊する滝に囲まれた円盤」から「隙間なく測量が終わった地球儀」へのアップグレード過程に対応しているのまた興味深い。言うなれば「オイラーの巾着袋(Euler drawstring bag)」の世界…
①理論上、その精度改善はクロード・シャノン(Claude Elwood Shannon, 1916年〜2001年)の情報理論いうところの1bitすなわち「(何とはなくいずれかの方角に)何かある(何もない訳ではなさそう)」なる超低解像度状態より始まったと考えられている。光学系(optics)でいうところも絞り(diaphragm)も最低状態からのスタートで被写界深度(DOF:Depth of field)も到底十分とはいえない出発地点。とはいえ判定の結果がその個体の生存に直接結びつくいているが故に、当初からそれは真摯に実効性を追求する実践的な取り組みとして発展してきたのである。
②情報量が増えるにつれ、それは「首振り(Zig-zag maneuver)などの無意識的行動の積み重ねによる立体視可能範囲の補完」といった努力を伴いつつ「正面に平面的に投影される情報窓」から次第に「観測原点をすっぽり包む全球型スクリーン」へと発展を遂げていく。その過程で「オイラーの原始量(Euler's primitive sweep)」は単純な一点透視図法には還元し得ない複雑怪奇な多様性を備える事になる。
③皮肉にも、この状況こそが(誰もが内面に備える)数学的直感と実際の数学や経済概念の乖離を生んでしまう。元来後者は、前者に導かれる形で数学者や物理学者が発展させてきたのだが、本当に精緻な形で言及しようとすればするほど色々と齟齬を生んでしまう。
第一の点は、〈数学の概念は、まったく予想外のさまざまな文脈のなかに登場してくる〉ということ。
The first point is that mathematical concepts turn up in entirely unexpected connections.しかも、予想もしなかった文脈に、予想もしなかったほどぴったりと当てはまって、正確に現象を記述してくれることが多いのだ。
Moreover, they often permit an unexpectedly close and accurate description of the phenomena in these connections.第二の点は、予想外の文脈に現れるということと、そしてまた、数学がこれほど役立つ理由を私たちが理解していないことのせいで、〈数学の概念を駆使して、なにか一つの理論が定式化できたとしても、それが唯一の適切な理論なのかどうかがわからない〉ということ。
Secondly, just because of this circumstance, and because we do not understand the reasons of their usefulness, we cannot know whether a theory formulated in terms of mathematical concepts is uniquely appropriate.〔この二つの論点をさらに言い直すと〕第一の点は〈数学は自然科学のなかで、ほとんど神秘的なまでに、途方もなく役立っているのに、そのことには何の合理的説明もない〉ということ。
The first point is that the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it.第二の点は〈数学の概念の、まさにこの奇怪な有用性のせいで、物理学の理論の一意性が疑わしく思えてしまう〉ということ。
Second, it is just this uncanny usefulness of mathematical concepts that raises the question of the uniqueness of our physical theories.こうした「数理モデル(Mathematical Models)」の特徴を「科学理論の客観性が保証される為には、その仮説が実験や観察によって反証される潜在性を備えていなければならない(逆をいえば科学理論とは、現段階ではきちんと反証を退けられている相応に信頼性の高い仮説の集合である)」と要約したカール・ポパー(Karl Raimund Poppr, 1902年〜1994年)の信念と結びつけたのが「数理モデル信仰(Belief in Mathematical Models)」となる。
そう、あくまで「信仰」の問題なので別種の「信仰」によって反対される可能性なら秘めている。しかもそれは「反証が成立されない限り、その仮説を棄却しない」と考える合理主義に立脚する「弱い」信仰なので「真理は最終的に必ず一つでなければならない」と考える「強い」信仰に対して決定的抵抗力を有している訳でもない。
*これが昨今日本を騒がせている「フクシマ不当差別問題」の本質とも。
①N(分割数)=1の時、観察対象の広がり(Expanse)、すなわち観測原点「0」からの視界(Perspective)は、とりあえず観測原点「0」から距離「1」先で任意の観測点と接する「半径πの円盤」と映る。これはまさに古代メソポタミア地方(チグリス・ユーフラテス川流域)や、エジプト王朝(ナイル川流域)やフェニキア人交易圏(地中海・黒海沿岸全域)や、ギリシャ人植民圏(ギリシャ半島中心にアナトリア半島やイタリア半島や南仏まで含む)や、古代ローマ帝国(地中海・黒海沿岸に加え中東進出を企てる)や、イスラム文化圏といった地中海沿岸地域を「文明圏」とし、これを「未開人が跋扈する辺境地帯」や「大海の向こう側にある世界の果て(絶えず滝の様に海水が流れ続けており、その向こう側で大海蛇(Giant Sea Serpent)が獲物が落ちてくるのを待ってる)」を同心円状に配置した正距方位図法(azimuthal equidistant projection)めいた古代地図の背後にあった地理感覚そのもの。
②Nが増大するにつれ、それは急速に観測原点「0」を観察対象「1」を中心に覆わんとする半球へと成長を遂げていく。実際には「半球」というより「3/4球」という感じ。そもそも複利計算式(1+1/N)^Nがベースになってるくらいだから、出足の伸びは物凄くグイグイ迫ってくる。かくして大航海時代以降「人類未踏の地」は急速に縮退し、20世紀に入ると南極やチョモランマ山渓、さらには深海や宇宙といった僻地に限定されるまでに至る。
③Nが十分に増大すると、それは観測原点「0」を覆う全球としか映らなくなるが、それでもなお決して極限値「−1」に到達する事はない。かくして「人類の認識可能範囲外を跋扈する絶対他者」は海底で眠る巨大怪獣や流星に付着して地球に到達する流行病、不可視の次元より襲来するフランク・ベルナップ・ロング「ティンダロスの猟犬(The Hounds of Tindalos、1929年)」における使役動物、さらには電波や放射能の類似物といった特殊な形態でしか存在し得なくなる。
まだ十分にまとめ切れていませんが、実際の歴史上における真の数概念の拡張はこういう具合になされてきた?