【数学ロマン】21世紀的現象学に欠かせない「三軸球面座標系」について。

そう、まさにこの領域…ある種の「数理的本懐」？

以下の論旨「安心感→適応感(Comfortable Feeling)」「危機感→違和感(Strange Feeling)」と代入するとこんな感じのルールセットが構成される。

「くすぐったがれる(すなわち、いかなる危機感も安心感を脅かす事のない適度な緊張状態)」状況へのフィードバック規則(カッコ内は共役ベクトル)

①適切な緊張感が保たれている状況下では、

安心感過剰時、あえて危機感を昂らせる(抑える)。

安心感過小時、あえて危機感を抑える(昂らせる)。

危機感過剰時、あえて安心感を昂らせる(抑える)。

危機感過小時、あえて安心感を抑える(昂らせる)。

②適切な危機感が保たれている状況下では、

安心感過剰時、あえて緊張感を昂らせる(抑える)。

安心感過小時、あえて緊張感を抑える(昂らせる)。

緊張感過剰時、あえて安心感を昂らせる(抑える)。

緊張感過小時、あえて安心感を抑える(昂らせる)。

③適切な安心感が保たれている状況下では、

危機感過剰時、あえて緊張感を抑える(昂らせる)。

危機感過小時、あえて緊張感を昂らせる(抑える)。

緊張感過剰時、あえて危機感を抑える(昂らせる)。

緊張感過小時、あえて危機感を昂らせる(抑える)。

ただし残念ながら人間の認識能力はこうした全貌の全てを同時ハンドリング可能な様には出来ておらず、ここにロジスティック方程式的に次元削減を遂行するメカニズムが関与してくる。

一方、「愛情と憎悪のバランス→適応感(Comfortable Feeling)」「好奇心と黙殺欲求のバランス→違和感(Strange Feeling)」と代入するとこんな感じのルールセットが構成される。

①適切な緊張感が保たれている状況下では、

愛情と憎悪のバランスが安定し過ぎてる時、あえて好奇心と黙殺欲求のバランスを揺さぶる(揺さぶらない)。

愛情と憎悪のバランスが不安定の時、あえて好奇心と黙殺欲求のバランスを揺さぶらない(揺さぶる)。

好奇心と黙殺欲求のバランスが安定し過ぎている時、あえて愛情と憎悪のバランスを揺さぶる(揺さぶらない)。

好奇心と黙殺欲求のバランスが不安定な時、あえて愛情と憎悪のバランスを揺さぶらない(揺さぶる)。

②好奇心と黙殺欲求のバランスが適切に保たれている状況下では、

愛情と憎悪のバランスが安定し過ぎてる時、あえて緊張感を昂らせる(抑える)。

愛情と憎悪のバランスが不安定の時、あえて緊張感を抑える(昂らせる)。

緊張感過剰時、あえて愛情と憎悪のバランスを揺さぶる(揺さぶらない)。

緊張感過小時、あえて愛情と憎悪のバランスを揺さぶらない(揺さぶる)。

③愛情と憎悪のバランスが適切に保たれている状況下では、

好奇心と黙殺欲求のバランスが安定し過ぎている時、緊張感を抑える(昂らせる)。

好奇心と黙殺欲求のバランスが不安定な時、あえて緊張感を昂らせる(抑える)。

緊張感過剰時、あえて好奇心と黙殺欲求のバランスを揺さぶる(揺さぶらない)。
緊張感過小時、あえて好奇心と黙殺欲求のバランスを揺さぶらない(揺さぶる)。

ただし残念ながら人間の認識能力はこうした全貌の全てを同時ハンドリング可能な様には出来ておらず、ここにロジスティック方程式的に次元削減を遂行するメカニズムが関与してくる。

こうした考え方の大元にある概念が以下。

①以下でいう「共役関係」とは「絶対値の等しい安心感と危機感の(一直線上における)正対」「絶対値の等しい愛情と憎悪の(一直線上における)正対」や「絶対値の等しい関心欲求と黙殺欲求の(一直線上における)正対」の様な評価軸に対応する。

実は符号的にどっちがプラス(正)でどっちがマイナス(負)かは「人間の主観としてしか存在しない」。実はまずこの現実こそが出発点だったりする。

②適正量の絶対値(Absolute Value)が等しい以上、ここに例記した「安心感と危機感」「愛情と憎悪」「関心欲求と黙殺欲求」の様な評価軸はさらに(二つの評価軸が直交する)XY-YX座標系において以下の範囲で(適正量近傍に単位円を描く)交項級数(Alternating Series)の軌跡、すなわち適正量の絶対値を半径rとする極座標系(Polar Coordinates System) $re^{θi}$ を構成する。

x=cos(0)=1の時、y=sin(0)=0
x=cos( $\frac{π}{2}$ )=0の時、y=sin( $\frac{π}{2}$ )=1
x=cos(π)=-1の時、y=sin(π)=0

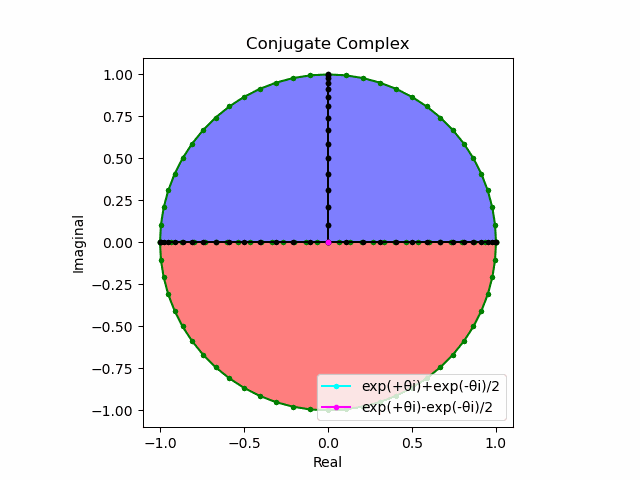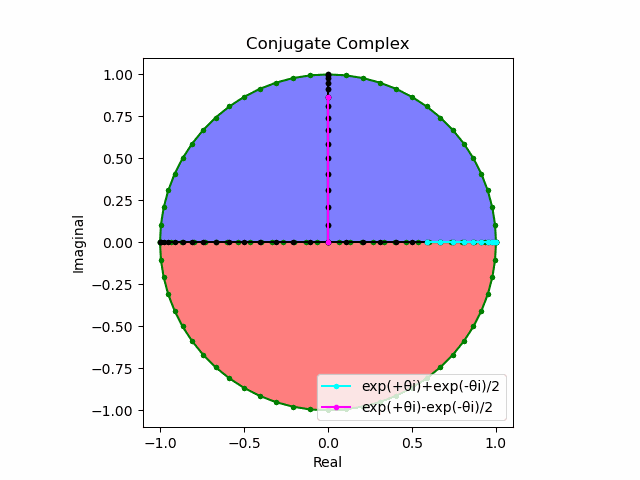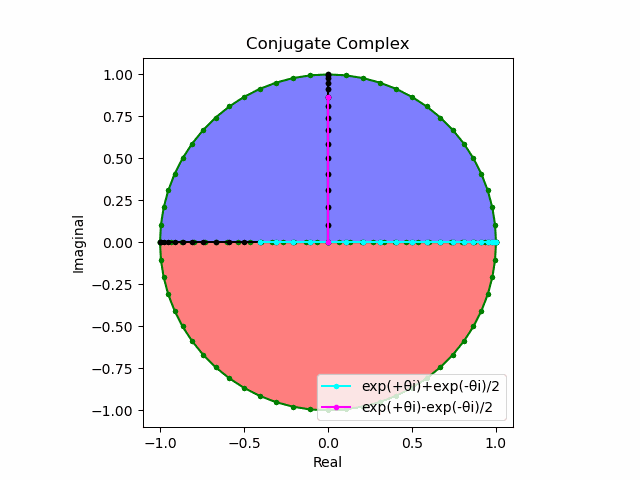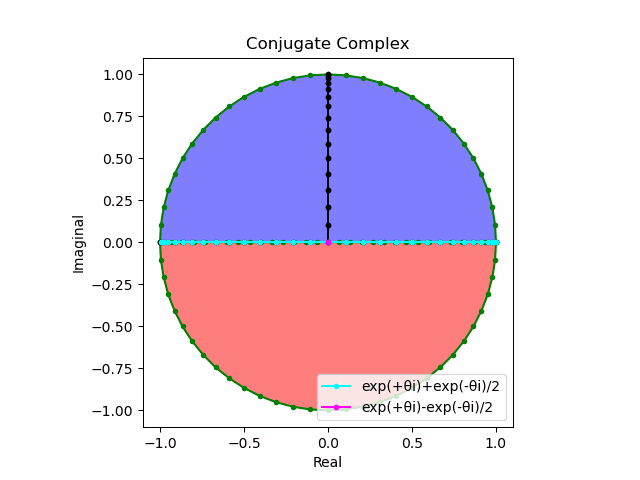
③そしてさらに上掲の極座標系のうち任意の二つを水平面で直行させ、これを赤道面=水平軸と設定すると、その対蹠対(Antipodes Set)がそれぞれ北極と南極に対応する第三の極座標系が垂直軸に現れてある種の球面座標系を構成する。

この球面座標系には3個の対蹠対(Antipodes Set)、すなわち合計６個の対蹠(Antipode)が存在し、それぞれを原点として対数写像(Logarithmic Map)を取ると評価軸i,j,k( $i^2=j^2=k^2=ijk=-1$ )について以下の交換関係(Commutation Relation)が成立する。

k=ij=-ji
j=ik=-ki
i=jk=-kj

まさにハミルトンの四元数(Hamiltonian Quaternion)そのものの考え方。以下では評価軸i,j,kをとりあえずこの様に設定する。

i=適応感(Comfortable Feeling)…数理的に偶関数や単位行列(線形代数)に対応。
j=違和感(Strange Feeling)…数理的に奇関数や回転行列(線形代数)に対応。
k=緊張感(Thrill)…i,jを直交座標系XY(正置=北極が原点)あるいはYX(転置=南極が原点)に重ねた場合の極座標的回転に対応。