「ドラゴン桜2(2018年〜)」に「積み残しが数学を難しくさせ、最後には嫌いにさせてしまう」という台詞がありました。例として挙げられていたのが以下の「三平方の定理の証明」…
具体的にはこんな感じ。
三平方の定理の証明
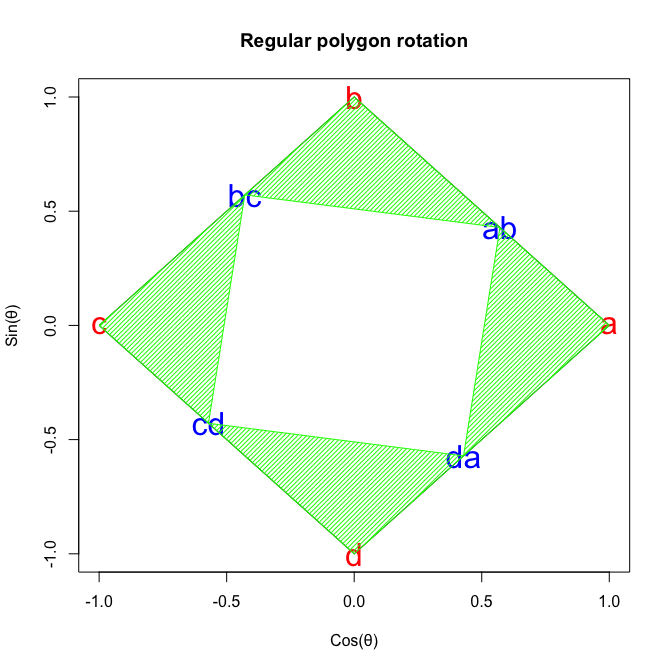
①直角三角形を4個集めると正方形が出来る。
②大きな正方形の面積Sは一辺が{a,ab}={b,bc}={c,cd}={d,da}(Aとする)で、かつ{ab,b}+{bc,c}+{cd,c}={da,a}(Bとする)にして{a,ab}+{ab,b}={b,bc}+{bc+b}={c,cd}+{cd,d}={d,da}+{da,a}なのでS=(A+B)^2
③またSは一辺が{ab,bc}={bc,cd}={cd,da}={da=ab}(Cとする)の正方形とABの直角三角形4つの和でもあるので
S=C^2+4*1/2*A*B
④よって
A^2+2AB+B^2=C^2+2AB
⑤これを整理すると
A^2+B^2=C^2
a^2+b^2=c^2からsinθ^2+cosθ^2=1へ
ここに登場する直角三角形ABCは(プログラム中での扱いを見ても分かる様に)以下とも置ける。
a=cos(θ)
b=sin(θ)
c=1
よって同時に任意の角度θに対して以下が成立。
cos(θ)^2+sin(θ)^2=1

ところで上掲の図形、真ん中に穴を開けてぐるりと回すと「基本円(Basic Circle 半径1の円)」に変形させられそうな気がしませんか?


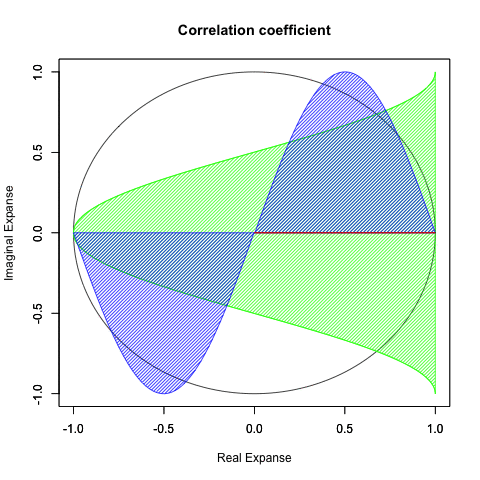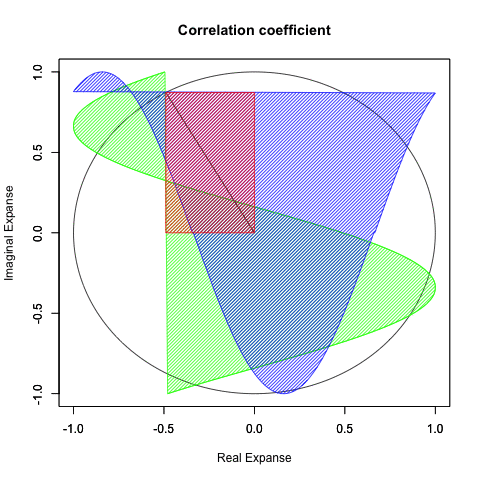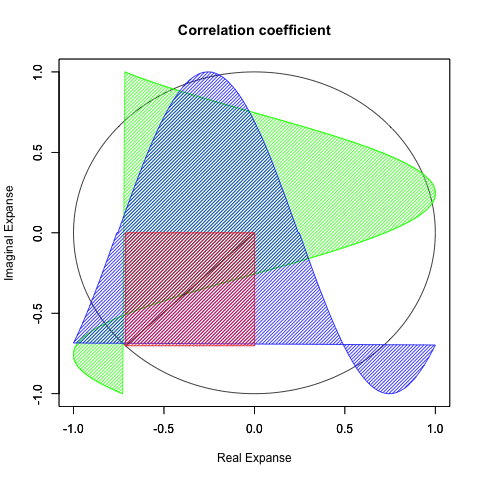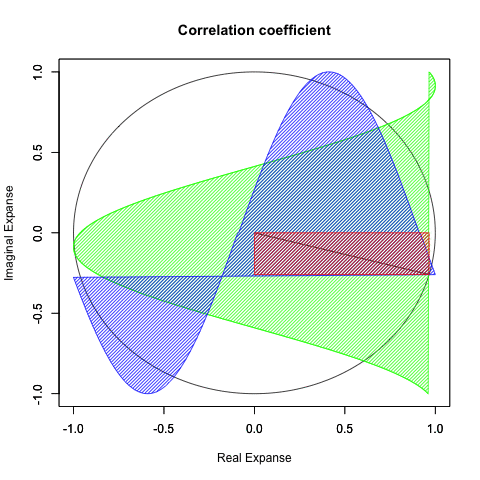
ならば両者の図形は位相幾何学(Topology)的にはどちらもドーナツ型、すなわちトーラス(単torus, 複tori)と見做せる事になるのです。

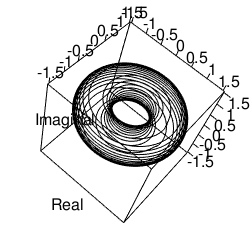
この時、すなわち0度(0ラジアン)から90度(π/2ラジアン)、90度(π/2ラジアン)から180度(πラジアン)、180度(πラジアン)から270度(3/4πラジアン)、270度(3/4πラジアン)から360度(2πラジアン)の4区画の遷移を単位としcos(θ)*sin(θ)の値が0と(sqrt(2)/2(0.7071068))^2=0.5の間を、cos(θ)+sin(θ)の値が1とsqrt(2)=1.414214の間を往復します。トーラス構造を読み解く鍵となるのはこのうち後者?
①正三角形と正方形は「連続トーラス(Multiplex Tori)」を構築する。
*そしてそれは綺麗に対数比をなしている。
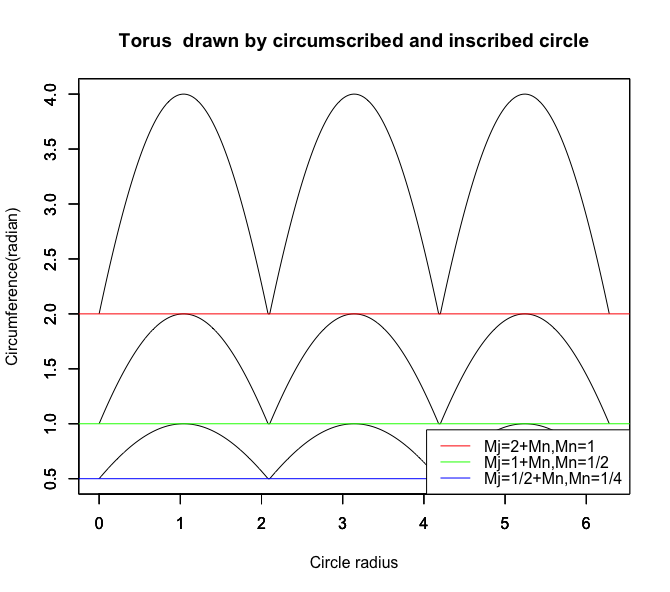
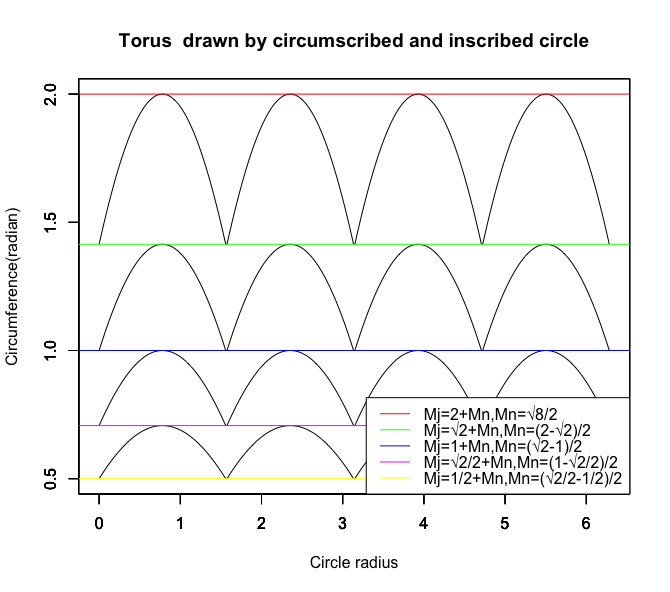
②正五角形以降は 「単層トーラス(Simplex Torus)」しか構築しない。
*より正確には「理論上それが構成されると考えるのは不可能でもないが、連鎖効果が見込めない為に普通は無視される」という感じかも。









こうした展開の極限として深淵ならぬ真円、すなわち「基本円(Basic circle、半径1の円弧)」の特徴に目を向けてみると…
- 外角の大きさpi/Nラジアンあるいは180/N度の値は0。
- 内角の大きさ2*pi*(N-2)/Nの値は2*piラジアン、180*(N-2)/Nの値は180度。
- 内接円と外接円の差cos(pi/N)の値も0で、辺長の合計が2*piと一致。
こうして全体像を俯瞰すると、ある意味「基本円(Basic circle、半径1の円弧)」は、それに内接/外接するあらゆる多角形の性質を継承してる訳ですが、参照されるのはほとんど(直角を扱う)正方形の特徴ばかりというのが興味深い?