【フーリエ変換】円柱から球面を経てトーラスに？

「フーリエ変換なら、どんな波形も合成出来る」。本当に？

円柱を描く

libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(0,2,length=3000)
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01") 

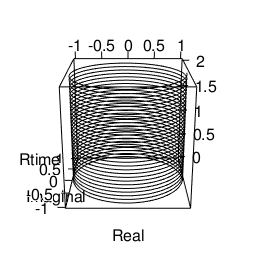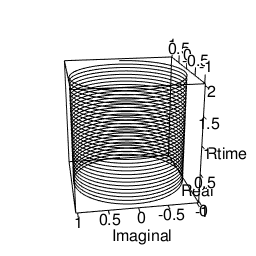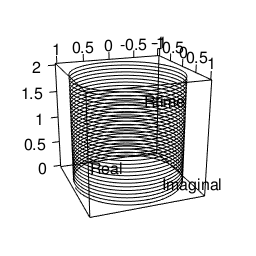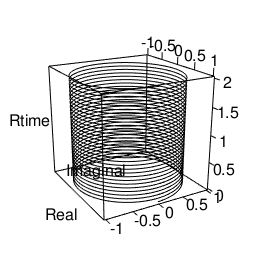
球を描く

libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-seq(0,2,length=3000)
#工夫
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=3000)
c1<-f1(c0)
#> plot(c0,c1,type="l",xlim=c(-1,1),ylim=c(0,1))
Real_c<-Real*c1
Imaginal_c<-Imaginal*c1

plot3d(Real_c,Imaginal_c,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01") 

トーラスを描くその１ 平面トーラス（折り返し円柱）を準備する。

libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
Real<-Re(f0(radians))
Imaginal<-Im(f0(radians))
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1.5,1.5),ylim=c(-1.5,1.5),zlim=c(-1.5,1.5))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test01") 

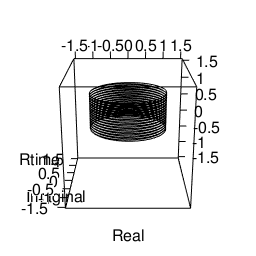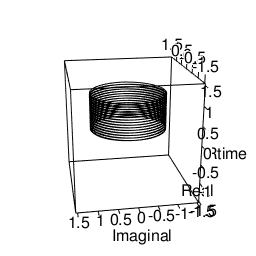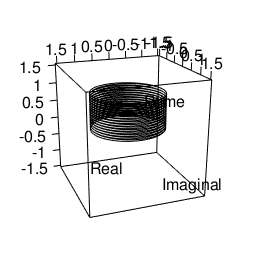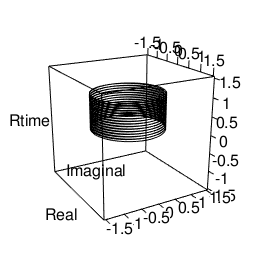
トーラスを描くその２ 平面トーラス（折り返し円柱）に曲率を設定。

libraly(rgl)
radians<-seq(0,60*pi,length=3000)
f0<-function(x){exp(x*(0+1i))}
r0<-f0(radians)
f1<-function(x){sqrt(1-x^2)}
c0<-seq(-1,1,length=1500)
c1<-c(f1(c0)/2,-1*f1(c0)/2)
#c1<-c(f1(c0),seq(0,0,length=1500))/2)
r1<-r0*(1+c1)
Real<-Re(r1)
Imaginal<-Im(r1)
Rtime<-c(seq(0,1,length=1500),seq(1,0,length=1500))
plot3d(Real,Imaginal,Rtime,type="l",xlim=c(-1.5,1.5),ylim=c(-1.5,1.5),zlim=c(-1.5,1.5))

movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test02") 

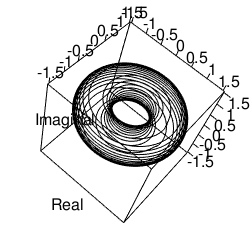
 確かに意外とやる…