「関数で円を描く」のは案外単純ではありません。
解析幾何学において「(a, b) を中心とする半径 r の円」は「(x-a)^2+(y-b)^2=r^2」を満たす点 (x, y) 全体の軌跡である。この方程式を、円の方程式と言う。これは、中心 (a, b) と円上の任意の点 (x, y) との二点間の距離が r であるということを述べたものに他ならず、半径を斜辺とする直角三角形にピタゴラスの定理を適用しすることで導出できる(直角を挟む二辺は、各座標の絶対差 |x − a|, |y − b| を長さとする)。
中心を原点に取れば、方程式は「x^2+y^2=r^2」と簡単になる。この形(x2, y2 の係数が等しく、xy の項を持たない)の方程式が与えられたとき、以下の何れか一つのみが成り立つ:
- ρ < 0 のときは、この方程式に解となる実点は存在しない。この場合を虚円(imaginary circle) の方程式と呼ぶ。
- ρ = 0 のとき、方程式 f(x, y) = 0 は中心となる一点 O := (a, b) のみを解とし、点円(point circle) の方程式と言う。
- ρ > 0 のときには、f(x, y) = 0 は O を中心とする半径 r := √ρ の円、あるいは実円 (real circle)の方程式になる。
α = 0 のとき f(x, y) = 0 は直線の方程式であり、a, b, ρ は(射影平面上で、あるいは見かけ上)無限大になる。実は、直線を「無限遠点を中心とする半径無限大の円」と考えることができる。
統計言語Rによる実証例
#「x^2+y^2=1」だけでは半円しか描けない
f0<-function(x){sqrt(1-x^2)}
plot(f0, xlim=c(-1,1),ylim=c(0,1),type="l",main="The Circle ploting x^2+y^2=1", xlab="x", ylab="y")

統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#円関数
yacas("Solve(Sqrt(x^2+y^2)-1,y)")
Yacas vector:
[1] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos(argument(1 - x^2)/2), sin(argument(1 - x^2)/2))
[2] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos*1
実際的な対応策は実にシンプル。プラス領域で半円を描く関数y=sqrt(1-x^2)のグラフとマイナス領域で半円を描く関数y=-sqrt(1-x^2)のグラフを同時表示すれば良いのです。
統計言語Rによる実証例
#y=-sqrt(1-x^2)のグラフ
f0<-function(x){-sqrt(1-x^2)}
plot(f0, xlim=c(-1,1),ylim=c(-1,0),type="l",main="The Circle ploting x^2+y^2=1(reverse)", xlab="x", ylab="y")

#y=sqrt(1-x^2)のグラフとy=-sqrt(1-x^2)のグラフの同時表示
f0<-function(x){sqrt(1-x^2)}
plot(f0, xlim=c(-1,1),ylim=c(-1,1),type="l",main="The Circle ploting x^2+y^2=1", xlab="x", ylab="y")
par(new=T)#上書き指定
f1<-function(x){-sqrt(1-x^2)}
plot(f1, xlim=c(-1,1),ylim=c(-1,1),type="l",main="", xlab="", ylab="")

問題は理論上この事が何を意味してるかなんですね。ここではxの動きに注目して見たいと思います。
- sqrt(1-x^2)関数は0(x=-1)で始まり0(x=1)で終わる。ピークはy=1の時でx=1
- -sqrt(1-x^2)関数も0(x=-1)で始まり0(x=1)で終わる。ピークはy=1の時でx=-1
円の角度と照会してみると…
統計言語Rによる作表例
target_names<-c("0 radian & 0 degree","π/2 radian & 90 degree","π radian & 180 degree","3/2π& 270 degree","2π & 360 degree")
target_values<-c("0","1","0","-1","0")
Circular_function<-data.frame(Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Circular_function), type = "html")
| Target_names | Target_values | |
|---|---|---|
| 1 | 0 radian & 0 degree | 0 |
| 2 | π/2 radian & 90 degree | 1 |
| 3 | π radian & 180 degree | 0 |
| 4 | 3/2π& 270 degree | -1 |
| 5 | 2π & 360 degree | 0 |
位相は90度ズレてますが、全く同じ振る舞いをする関数があります。三角関数に分類されているコサイン関数cos(Θ)がそうですね。
統計言語Rによる作表例
target_names<-c("0 radian & 0 degree","π/2 radian & 90 degree","π radian & 180 degree","3/2π& 270 degree","2π & 360 degree")
target_values<-c("1","0","-1","0","1")
Circular_function<-data.frame(Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Circular_function), type = "html")
| Target_names | Target_values | |
|---|---|---|
| 1 | 0 radian & 0 degree | 1 |
| 2 | π/2 radian & 90 degree | 0 |
| 3 | π radian & 180 degree | -1 |
| 4 | 3/2π& 270 degree | 0 |
| 5 | 2π & 360 degree | 1 |
統計言語Rによる実証例
#複素平面(球面)
Complex_plane<-function(x){
ifelse*2
theta <- c(seq(0, pi, length=180),seq(-pi, 0, length=180))
dr<-seq(0,2*pi,length=360)theta00<- seq(1, -1, length=360)
theta01 <- c(theta[x:360],theta[1:x-1])
theta_cos<-cos(theta01)
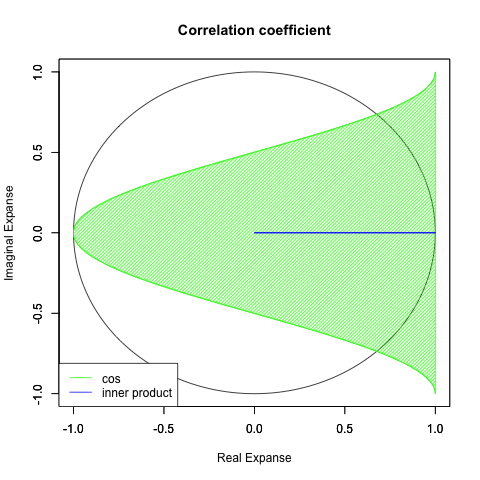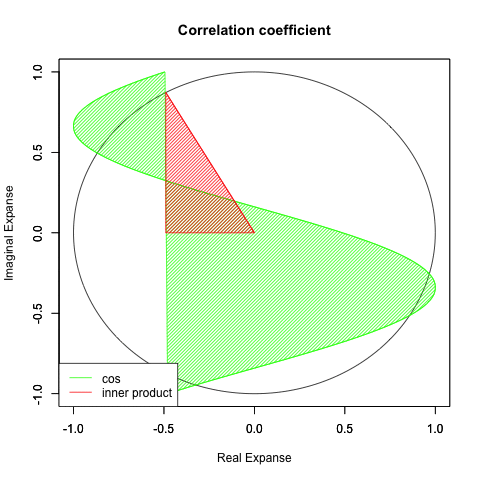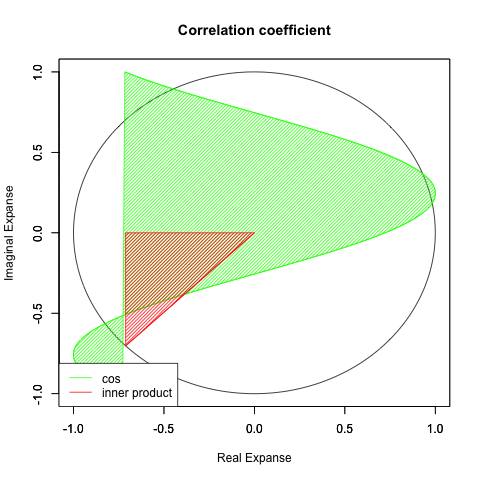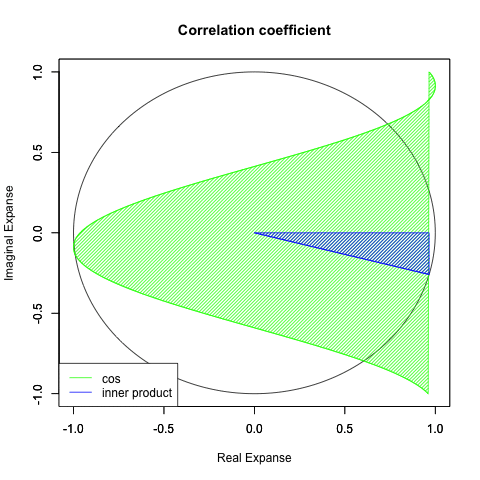
plot(cos(theta), sin(theta), xlim=c(-1,1), ylim=c(-1,1), type="l", main="Correlation coefficient",xlab="Real Expanse", ylab="Imaginal Expanse")
par(new=T)#上書き指定
plot(theta_cos,theta00,xlim=c(-1,1), ylim=c(-1,1), type="l",col=rgb(0,1,0),main="",xlab="", ylab="")
#cos(x)を塗りつぶす
polygon(theta_cos, #x
theta00, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
#線を引く
segments(cos(dr[x]),sin(dr[x]),0,0,col=segC)#内積を塗りつぶす
polygon(c(cos(dr[x]),cos(dr[x]),0), #x
c(sin(dr[x]),0,0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=segC) #塗りつぶす色
legend("bottomleft", legend=c("cos", "inner product"), lty=c(1,1),col =c(rgb(0,1,0),segC))}
#アニメーションさせてみる。library("animation")
Time_Code=c(1,15,30,45,60,75,90,105,120,135,150,165,180,195,210,225,240,255,270,285,300,315,330,345)
saveGIF({
for (i in Time_Code){
Complex_plane(i)
}
}, interval = 0.1, movie.name = "TEST.gif")
要するにそれはこういう事なのです。

①コサイン関数cos(Θ)の推移は統計学でいう相関係数そのもの。すなわち「0ラジアン=0度」の時に正の相関係数(2つの変数の一方が増減するにつれ、対象変数もそれに従って増減する関係)が最大の「1.0」を迎え、「πラジアン=180度」の時に負の相関係数(2つの変数の一方が増減するにつれ、対象変数がその真逆に増減する関係)が最小の「-1.0」を迎える。
②すなわちどちらの世界観においても相関係数「0」はそれより先がない極限値となる。これを数学的には「軸が直交する」あるいは「線型独立関係にある」という。
線型独立(linearly independent)または一次独立 - Wikipedia
線型代数学(linear algebra)において、ベクトルの集合が線型従属(一次従属)でないこと、つまり集合のベクトルの線型結合によるゼロベクトルの表示が自明なものに限ることをいう。
例:ベクトル空間 R2 の部分集合 {(1, 0), (0, 1), (-2, 1)} は非自明な線型関係 2(1, 0) - (0, 1) + (-2, 1) = 0 を満たすので線型従属である。他方 {(1, 0), (0, 1)} は線型独立である。
地理的な例は線型独立性の概念を明確にする助けとなるだろう。ある場所の位置を記述している人は「それはここから3キロ北で4キロ東」と言うかもしれない。これは位置を記述するのに十分な情報である、なぜならば地理的な座標系は 2-次元ベクトル空間と考えることができるからである(高度と地球の表面の曲がりは無視して)。その人は「その場所はここから北東に5キロ」と付け加えるかもしれない。この主張は正しいが、必要でない。
この例において「3キロ北」ベクトルと「4キロ東」ベクトルは線型独立である。つまり、北ベクトルを東ベクトルの言葉では記述できないし、逆もまたしかり。三番目の「5キロ北東」ベクトルは他の 2 つのベクトルの線型結合であり、ベクトルの集合を「線型従属」にする、つまり、3つのベクトルのうち1つは不要である。
また次のことにも注意しよう。高度が無視されない場合、線型独立な集合に第三のベクトルを付け加えることが必要になる。一般に、n 個の線型独立なベクトルは n-次元空間の任意の位置を記述するために必要である。
文学の世界には「愛の反対は憎悪、それとも無関心?」なる問い掛けが存在し得ますが、数理の世界における解(Solution)は至ってシンプル。
- 愛と憎悪の関係を、本来なら素直に喜ぶべき局面でドス黒い嫉妬心が渦巻く状況と捉えるなら、前者は「正の相関」。後者は「負の相関」と捉えられる。
- どちらの感情も湧かないのが完全なる「無関心状態」で、そこには如何なる形でも感情の再生産も起こり得ない。
一方、この概念の導入により「オイラーの原始量(Euler's primitive sweep)」は「直行する座標軸」を獲得し、次の段階へと進んでいくのです。
