ネット上の数学世界界隈あるある…

人類史上もっとも美しい式、オイラーの等式についても、教えてくれたのは彼女だった――
— 阿良々木暦 (@Araragi219) April 8, 2019
オイラーの等式、こんな風に随所で強烈に持ち上げられながら、実際には「オイラーの等式の特別解」程度の言及で逃げてしまうケースが大半だったりします。何しろ本当に「神=人類に認識可能な世界の外側を跋扈する絶対他者と人類(というより生物の進化)との不可分な紐帯」を扱う恐ろしい式なので、文字通り「(その不可解さ故に敬いながら遠ざける)敬遠感情の対象」にされてしまっているのです。
オイラーの公式は、物理学者のリチャード・ファインマンによって「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」と評されたことで有名です。
まず一般的アプローチについて統計言語Rで検証してみましょう。
#オイラーの方程式
complex(real=cos(pi*0.5),imaginary=sin(pi*0.5)) #ラジアン表記で90度
[1] 0+1i
#特殊解としての「オイラーの等式」
exp(pi*complex(real=0,imaginary=1))
[1] -1+0i
確かに素晴らしいのですが、複素座標上の円の軌跡が(互いに直行する)Cos波とSin波の合成で再現可能な事を前提とした時点で、もはや何処にも「奴」すなわち「我々の認識可能範囲外を跋扈する絶対他者」の居場所がありません(すなわちx座標とy座標の直行を既に前提として受容済みの2次元(面の世界)世界での出来事)。それに対しオイラーの等式は以下のシステムによって「任意の観測原点が何らか観測対象の捕捉に成功した事によって認識範囲が0次元(点の世界)から(最低でも)1次元(線の世界)に拡張される瞬間」を扱っているのが特徴となります。
- 任意の観測原点「0」を設置する。この時点ではまだ何も起こってはいない。
*ヤコブ・ベルヌーイが自然対数eの導出に用いた指数関数の計算式(1+1/N)^Nの大源流は複利計算だが、そもそもこの計算式自体「元手=0」だと「元手に対する利息」も0となって計算自体が成立しないのである。
- 何か優位な観測結果が得られた事によって観測原点「0」との間に広がり(Expanse)が発生。この段階では比較対象が存在していないので、それが如何なる距離でも基準値「1」となる。また角度の概念も存在していない。
*おそらく宗教次元における「1にして全」「全にして1」なる感覚の大源流にある何か。そしてこの概念は所謂「生存バイアス問題」と結びついていく。生物がこうした原理と紐付けられたのはおそらく「目とそれから得た情報を処理する脊髄」を備えた生物が登場したカンブリア爆発時代。当時食物連鎖の頂点にあった捕食動物アノマロカリスは、何らかの形でここでいう「1」への到達を通じて当時最大最強の生物の座を獲得し(ライバル等の登場により)その優位を手放さざるを得なくなった結果あっけなく滅び去っていった。その意味合いにおいてアノマロカリスは今日における「ビジネスモデル」の大源流ともいえそうなのである。アノマロカリス(Anomalocaris) - Wikipedia
約5億2,500万- 約5億0,500万年前、古生代カンブリア紀の海に棲息していた捕食性動物。完全復元される以前から触手の化石は以前から発見されており、当初はエビの仲間の腹部と考えられたことから、1892年にカナダの古生物学者であるジョセフ・フレデリック・ホワイティーブス(Joseph Frederick Whiteaves)によって「anomalo- (奇妙な) + caris (エビ)」、すなわち「奇妙なエビ」との意味で Anomalocaris(Anomalocaris canadensis)という学名を与えられた。中国語でも「奇蝦(きか)」である。

その後、バージェス動物群(約5億0,500万年前)の代表的動物として広く一般に知られるようになったが、更に古い時代に属する澄江動物群(約5億2,500万- 約5億2,000万年前)にも、アノマロカリス属と思われる種類がいくつか発見されている。一方で、バージェス頁岩累層より新しい地層からの出土はほとんど無い。
最大の個体は約1メートルにも及ぶと推測され、既知カンブリア紀最大の動物であり、当時の頂点捕食者(生態ピラミッドの最高次消費者)であったと考えられる。
直接と思われる子孫を残さずに絶滅した動物群に属するものであり、かつては所属タクソン(分類群)不明の「プロブレマティカ(不詳化石)」の代表例として語られてきた。その後は研究が進んでおり、他のアノマロカリス類などと共に、基盤的な節足動物であると認められ、節足動物の起源に繰り広げる議論において重要視される古生物になった。*この生物がどうして成功し、かつあっけなく滅んでいったかについて真相は定かではない。また全ての生存バイアスに具体的理由が伴うとも限らない。とはいえあらゆる「ビジネスモデル」と「数理モデル」の根底には確実に「欠かせない/有意な/意義ある(Significantly)事象」と「黙殺し得る/有意でない/無意味な(ignorable)事象」を峻別する何らかのシステムが不可欠であり、この(後期ハイデガーいうところの)集-立(Gestell)システム(特定意図実現の為に手持ちリソースを総動員しようとする体制)に先行して存在する「想像上のアノマロカリス(Imaginary Anomalocaris)」の階層だけが伝統主義やヒューリスティック(英heuristic, 独Heuristik)な解法を含み得る点だけが重要なのである。
伝統主義やヒューリスティック(英heuristic, 独Heuristik)な解法…思えば「物語」の起源からしてこれである。一時期あれほどの繁栄を誇った古代エジプト王朝は、十字軍運動ばかりか英仏内政にまで干渉したリュジニャン家は、シチリア王国をも支配下に置いた神聖ローマ帝国皇統ホーエンシュタフェン家は、日本の平氏はどうして零落を余儀なくされたのか? 彼らにとって「1」とは何だったのか? そういう事を気にする名家、すなわち伝統的にインテリ=ブルジョワ=政治的エリート階層を構築してきた王侯貴族や聖職者の家系が物語消費の主体だった時代には、幽霊も主に「没落した末裔の救済を求めて権力者に粘着する」形で出現したという逸話が興味深い。
*そして産業革命到来によって消費経済の主要な担い手が個人主義者の庶民に推移すると、今度はナポレオン・ヒル「思考は現実化する(Think and Grow Rich、初版1987年)」が国際的ベストセラーに。
- とりあえずこの状況を「オイラーの原始円/球面(Euler’s primitive circle/spherical surface)」とでも呼ぶ事にする。この段階において広がり(Expanse)「1」は観測原点「0」を中心とする半径「1」の同心円/球としてイメージされるからである。
*この「オイラーのドラムスティック(Euler's Drum sticks)の先端(観測原点より距離「1」だけ離れた地点)の旋回範囲」という概念こそが統計学や量子力学との接点となる。
そしてこの状態においてのみ任意の観測点「1」と観測原点「0」を通る直径「2」の線分の先、あるいはラジアン表記による「π」、すなわち同心円/球の半周先に存在する筈と仮定される極限値「−1」が想定可能となる。
*そう、このシステムにおいては「奴」すなわち「我々の認識可能範囲外を跋扈する絶対他者」はそういう形で顕現化してくるのである。#オイラーの原始円/球(Euler’s primitive circle/sphere)
theta <- seq(pi, -pi, length=360)
plot(cos(theta), sin(theta), type="l",col=rgb(0,1,0), main="Euler’s primitive circle/sphere", xlab="Real Expanse", ylab="Imaginary Expanse")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
小学校の頃、ユークリッド幾何学に基づいて「線分とは2点間の間にたった一つだけ存在する最短距離である」と教わりましたが、実際に「1」がどうやって発見されたかについて突き詰めて考えていくとこういうシステムへと到達してしまう訳ですね。これがまさに(今日の数学からは相対的に省みられる機会が減少した)指数関数・対数関数・複素数の世界。そこでは観測原点「0」と観測対象「1」を結ぶ線分だけが「(実在する対象のみに立脚する)実数解(Real solutions)」であり、観測対象を点として特定するとオイラーの原始円/球面(Euler’s primitive circle/spherical surface)上を半周した先や観測原点「0」と観測対象「1」を結んだ線分の延長線上に現れる「−1」は「(想定上においてのみ存在する)虚数解(Imaginary solutions)」に分類される事になるのです。
*まだ確証までは至ってないが、実はこうした諸概念は最終的にガウス平面に0から始まり無限大に至るZ軸を加えたリーマン球面(Riemann sphere)へと発展的に解消されていくのかもしれない。
それでは「1」の具体的振る舞いは? ここではWikipediaにある以下の記述から出発したいと思います。
*この証明法自体、不思議なまでに一般的な数学入門書では目にする事がない気がするのは気のせい?
オイラーの等式(Euler's identity) - Wikipedia
指数関数 e^z は (1+z/N)^NのN が無限に大きくなるときの極限として定義でき、e^iπは その極限値となる。このアニメーションでは、N の値を1から100まで増加させている。複素数平面において1 + iπ/Nの累乗を点で表示しており、折れ線の端点が (1+iπ/N)^Nとなる。これにより、N の増加に伴って (1 + iπ/N)^N が−1に近付く様子が観察される。
統計言語Rで追証してみましょう。そもそも上掲の式はヤコブ・ベルヌーイが自然対数eの導出に用いた複利計算式(1+1/N)^Nに立脚しています。
Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)}
theta <- seq(pi, -pi, length=360) #円周率(ラジアン表記)Eulers_identity00_plot<-function(n){
plot(cos(theta), sin(theta), xlim=c(-2,1),ylim=c(0,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定plot(Re(Eulers_identity(n)),Im(Eulers_identity(n)),xlim=c(-2,1),ylim=c(0,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}#アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
Eulers_identity00_plot(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

一方、オイラーはネイピアの対数表の底「0.9999999」から出発してるので、最初は(1-1/N)^Nの計算式でこの問題を解いたと考えられています。
Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a-a*b}, Tarm, accumulate = T)}
theta <- seq(pi, -pi, length=360) #円周率(ラジアン表記)Eulers_identity00_plot<-function(n){
plot(cos(theta), sin(theta), xlim=c(-2,1),ylim=c(-4,0),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定plot(Re(Eulers_identity(n)),Im(Eulers_identity(n)),xlim=c(-2,1),ylim=c(-4,0),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}#アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
Eulers_identity00_plot(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

この2つの計算結果は複素図表上において共役関係にあります。
まぁ要するに「オイラーの原始円/球面(Euler’s primitive circle/spherical surface)」において同一平面上にあるので、その振る舞いに数多くの共通点が見られるという事ですね。
#オイラーの等式(全周分)
Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)}
theta <- seq(pi, -pi, length=360) #円周率(ラジアン表記)
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta), xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}#アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

これはすなわち、観測対象「1」を中心とする観測原点「0」の視界(Perspective)範囲の変化そのものを表しているといえましょう。
#オイラーの等式(全周分)
Eulers_identity<-function(n){
rim01<-pi*complex(real=0,imaginary=1)
Tarm=c(complex(real=1,imaginary=0),seq(rim01/n,rim01/n,length=n))
Reduce(function(a,b) {a+a*b}, Tarm, accumulate = T)}
theta <- seq(pi, -pi, length=360) #円周率(ラジアン表記)
#グラフを描画してみる。
Eulers_identity01_plot<-function(n){
ei01<-Eulers_identity(n)
ei02<-Conj(ei01)
plot(cos(theta), sin(theta), xlim=c(-2,1),ylim=c(-4,4),type="l",col=rgb(0,1,0), main="Euler’s identity", xlab="Real Expanse", ylab="Imaginary Expanse")
par(new=T) # 上書き指定
plot(Re(ei01),Im(ei01),xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
par(new=T) # 上書き指定
plot(Re(ei02),Im(ei02),xlim=c(-2,1),ylim=c(-4,4),type="l",main="", xlab="", ylab="")
#観測原点からの視界(Perspective)追加。
Expanse01<-c(1,Re(ei01),0,rev(Re(ei02)),1)
Expanse02<-c(0,Im(ei01),0,rev(Im(ei02)),0)
polygon(Expanse01, #x
Expanse02, #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0)) #塗りつぶす色
text(0, 0, "0",col=rgb(0,0,0))
text(1, 0, "1",col=rgb(0,0,1))
text(-1, 0, "-1",col=rgb(1,0,0))
text(0, 1, "π",col=rgb(0,1,0))
text(0, -1, "π",col=rgb(0,1,0))
segments(0,0,1,0,col=rgb(0,0,1))
segments(0,0,-1,0,col=rgb(1,0,0))
}#アニメーションさせてみる。
library("animation")
Time_Code=c(1,2,4,8,16,32,64,128)
saveGIF({
for (i in Time_Code){
Eulers_identity01_plot(i)
}
}, interval = 0.1, movie.name = "TEST.gif")

①N(分割数)=1の時、観察対象の広がり(Expanse)、すなわち観測原点「0」からの視界(Perspective)は、とりあえず観測原点「0」から距離「1」先で任意の観測点と接する「半径πの円盤」と映る。

- ところでこの世界観、何処かで見覚えがないだろうか? そう、まさにこれは古代メソポタミア地方(チグリス・ユーフラテス川流域)や、エジプト王朝(ナイル川流域)やフェニキア人交易圏(地中海・黒海沿岸全域)や、ギリシャ人植民圏(ギリシャ半島中心にアナトリア半島やイタリア半島や南仏まで含む)や、古代ローマ帝国(地中海・黒海沿岸に加え中東進出を企てる)や、イスラム文化圏といった地中海沿岸地域を「文明圏」とし、これを「未開人が跋扈する辺境地帯」や「大海の向こう側にある世界の果て(絶えず滝の様に海水が流れ続けており、その向こう側で大海蛇(Giant Sea Serpent)が獲物が落ちてくるのを待ってる)」を同心円状に配置した正距方位図法(azimuthal equidistant projection)めいた古代地図の背後にあった地理感覚そのものなのである。


正距方位図法(azimuthal equidistant projection)
飛行機の最短経路や方位を見るために使われる。図の中心から他の1地点を結ぶ直線が、図の中心からの正しい方位、最短経路を表し、図の中心からの距離を正しく求めることができる。
*「大航海時代(Age of Discovery、15世紀中旬〜17世紀中旬)」の発端となったのは十字軍運動(11世紀初頭〜15世紀中旬)終焉と黒死病大流行(15世紀)のせいで(人口減少によって)農業立国の道も(国際交易量激減によって)商業立国の道も閉ざされたイベリア半島の「騎士修道会国家」ポルトガルの決死の起死回生策だった「アフリカ十字軍(1415年〜1440年代)」だった。この過程でそれまで「不帰の岬」として恐れられてきた西サハラのボジャドール岬(1434年)を越え1488年には喜望峰へと到達。かくして欧州は「Giant Sea Serpentsの壁」を乗り越えるパラダイムシフトを達成した。

②Nが増大するにつれ、それは急速に観測原点「0」を観察対象「1」を中心に覆わんとする半球へと成長を遂げていく。
*実際には「半球」というより「3/4球」という感じ。そもそも複利計算式(1+1/N)^Nがベースになってるくらいだから、出足の伸びは物凄くグイグイ迫ってくる。


*こうした展開はある意味近世以降の欧州において「未踏の地」が急速に減少し、20世紀に入ると南極やチョモランマ山渓、さらには深海や宇宙といった僻地に限定されていくプロセスに対応。
③Nが十分に増大すると、それは観測原点「0」を覆う全球としか映らなくなるが、それでもなお決して極限値「−1」に到達する事はない。
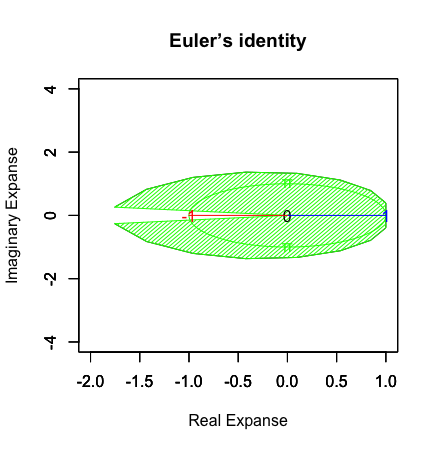
*かくして「人類の認識可能範囲外を跋扈する絶対他者」は海底で眠る巨大怪獣や流星に付着して地球に到達する流行病、不可視の次元より襲来するフランク・ベルナップ・ロング「ティンダロスの猟犬(The Hounds of Tindalos、1929年)」における使役動物、さらには電波や放射能の類似物といった特殊な形態でしか存在し得なくなる。
そろそろお気付きでしょうか、こうした検討を経て浮かび上がってくる虚数解(
Imaginary solutions)の視界とTVゲームの世界におけるFPS(First-Person Shooter)やTPS(Third-Person Shooter)の視界の類似性に。
*FPS(First-Person Shooter)の視界は、ここでいう「0」の視界そのもの。

TPS(Third-Person Shooter)の視界は、ここでいう「−1」の視界そのもの。
要するに「Imaginal(想像上の)」とはこうした意味合いにおける「外界とのインターフェイス(操縦席)」の事でもある訳です。こうした観点が来るべき「VR(Virtual Reality)の時代」には益々重要となってくるんじゃないでしょうか?


