私の時空間にまつわる源イメージはあくまでこれです。
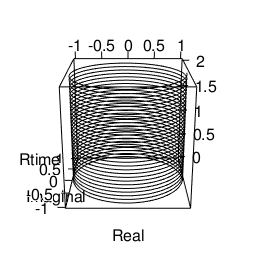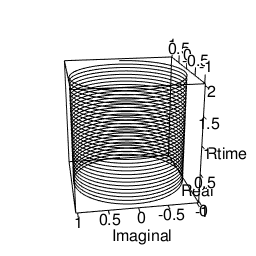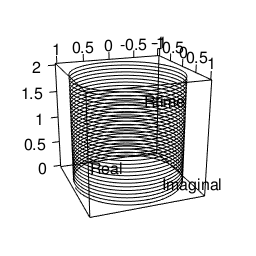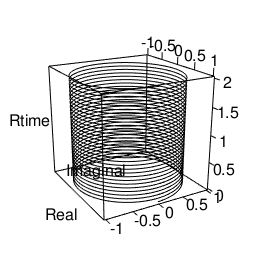
- 数直線なるもの、その目盛りの反復単位に応じた螺旋構造としてイメージ可能。
*要するに半径R=1の基本円の円弧2πの空間移動で度数を表示するラジアン法を全ての単位の基底に置く。するとラジアン毎秒(Radian/s)の単位が桁上がりに対応する事になる。 - 無論、実際に目盛りをどう振るかは全て観察者の主観に任されている。
*観察対象は様々な形態における「反復可能単位(周期)」を供給するに過ぎない。
位取り記数法もしくはもしくはN 進法 - Wikipedia
数の表現方法の一種で、予め定められたN 種類の記号(数字)を列べることによって数を表す方法である。(位取りのことを桁ともいう。)数の表現方法の一種で、予め定められたN 種類の記号(数字)を列べることによって数を表す方法である。(位取りのことを桁ともいう。)
今日の日本において通常使われているのは、 N が十である十進法であるが、コンピューターでは二進法、八進法、十六進法といった「二の冪数」進法が用いられている。用語としては、「十進法」など「N進法」は「N進位取り記数法」を意味する語ではあるが、記数法以外にも「N進(Nで桁上がりする)命数法」という意味や、単に「ある特定の単位から上の単位を作る、冪乗による規則」という意味でも使用される。一方「N進法」はほぼ「base-N positional system/N進位取り記数法」の意味でしか使われない。
p進数
N進表記と関連が深い概念として、素数p毎に定まるp進数というものもある。 別概念ではあるが、両者は非常に関連があり、整数の p進表記を(可算)無限桁の自然数の範囲に拡張したものが p進整数で、さらにそこに有限桁の小数部分を許したものが p進数となる。ただし「無限桁の整数」(の一部は有理数として再解釈できるもののほとんど)は普通の数(実数)とは異なる。
p進数(p-adic number) - Wikipedia
1897年にクルト・ヘンゼルによって導入された、数の体系の一つである。文脈によっては、その体系の個々の数を指して p 進数と呼ぶこともある。
有理数の体系を実数や複素数の体系に拡張するのとは別の方法で各素数 p に対して p 進数の体系が構成される。それらは有理数のつくる空間の局所的な姿を記述していると考えられ、数学の中でも特に数論において重要な役割を果たす。数学のみならず、素粒子物理学の理論などで使われることもある。
「p 進数」とは「2進数」や「3進数」の総称に過ぎないので、文字 p がすでに他の場所で用いられている場合、q 進数や l 進数などと表現されることもある。
なお、自然数や実数を 0 と 1 で表現する方法(2進法)やその結果得られる記号列(2進列)も「2進数」と呼ぶ場合があるが、本項の意味での「2進数」とは異なる。
例えば、お遊びとしては「三進数系の世界」なんてのも考えられる訳です。




実際、広く普及してるのは以下あたり?
①二進数系の世界…コンピューターが実際に稼働してる環境。



あまりに味気ないので、補助的な「上級目盛りへの置換」も盛んに行われています。
四進数


八進数


十六進数


②10進数の世界…厳密にいうと素数ベースではないが、多くの人間に最も親しまれている表示方法?

10進数、小数点なし

10進数、小数点あり

③12進数の世界…厳密にいうと素数ベースではないが、例えば音楽理論の世界。純正律(Just Intonation)と平均律(Equal Temperament)のズレなんて問題も抱える。


この最後の一文まで混乱する事なく辿り着けた人なら、冒頭で私が何を言おうとしてたのか既に納得済みなのでは? 多くのSF作品において異星人は「3進数系」や「5進数系」や「7進数系」を用いていると設定されますが、それも人類に馴染みのない進数系が(人類と心の在り方が異なる)エイリアンらしさを引き立てるからなんですね。
H・G・ウェルズ「宇宙戦争(The War of the Worlds、1898年)」に登場するエイリアンは伝統的に「三進数系で思考する」と描写されてきた。

H.P.ラヴクラフト「狂気の山脈にて(At the Mountains of Madness、執筆1931年、初出1936年、完全版発表1985年)」に登場する「旧支配者(Elder Thing)」の頭部は五芒星型とされる。

テッド・チャンのSF短編小説「あなたの人生の物語(Story of Your Life、1998年)」に登場する異星人ヘプタポッドは「7本足」である。

こうした形での人類の想像力の限界すら乗り越ようとするのが「数学の世界」?