今回は三平方の定理、すなわちいわゆる「ピタゴラスの定理」の証明から。
三平方の定理の証明
①直角三角形を4個集めると正方形が出来る。
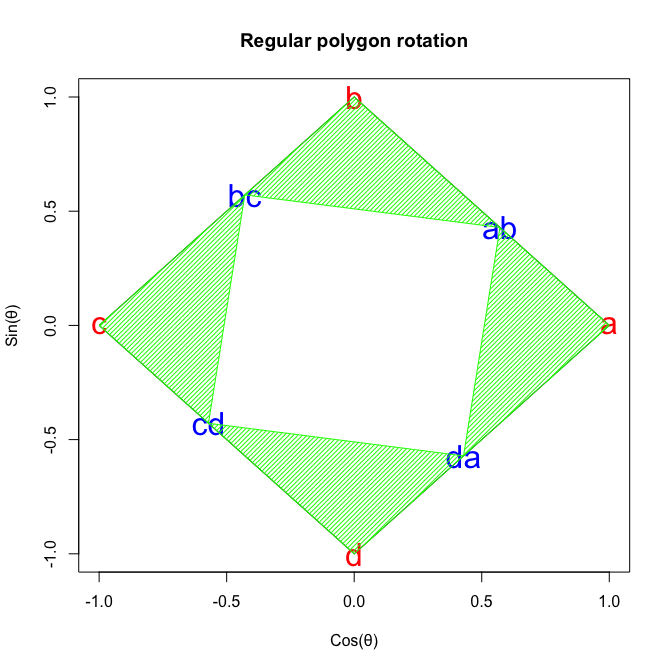
②大きな正方形の面積Sは一辺が{a,ab}={b,bc}={c,cd}={d,da}(Aとする)で、かつ{ab,b}+{bc,c}+{cd,c}={da,a}(Bとする)にして{a,ab}+{ab,b}={b,bc}+{bc+b}={c,cd}+{cd,d}={d,da}+{da,a}なので
S=(A+B)^2
③またSは一辺が{ab,bc}={bc,cd}={cd,da}={da=ab}(Cとする)の正方形とABの直角三角形4つの和でもあるので
S=C^2+4*1/2*A*B
④よって
A^2+2AB+B^2=C^2+2AB
⑤これを整理すると
A^2+B^2=C^2
a^2+b^2=c^2からsinθ^2+cosθ^2=1へ
ここに登場する直角三角形ABCは(プログラム中での扱いを見ても分かる様に)以下とも置ける。
a=cos(θ)
b=sin(θ)
c=1
よって同時に任意の角度θに対して以下が成立。
cos(θ)^2+sin(θ)^2=1

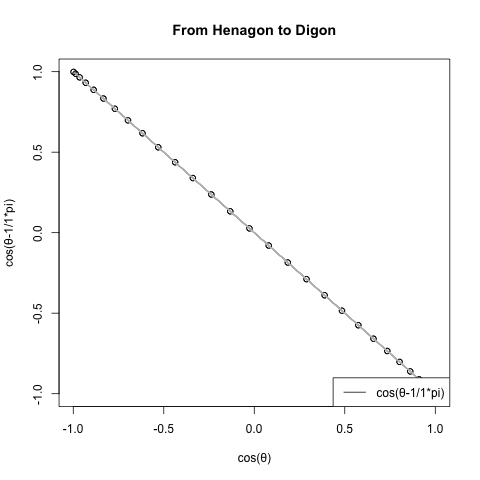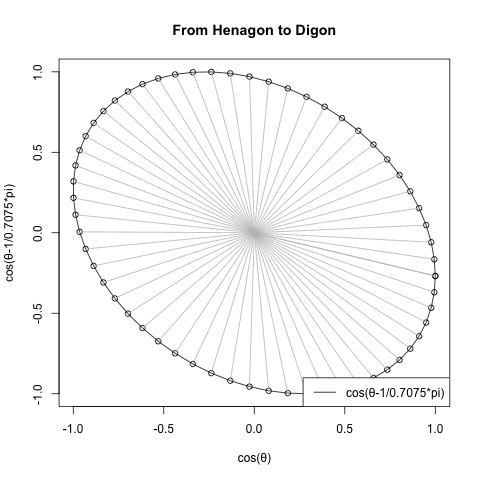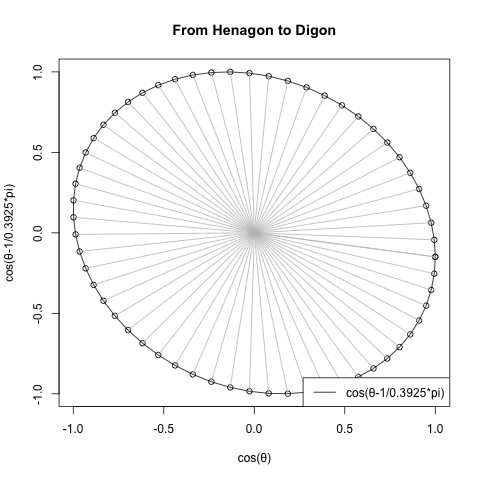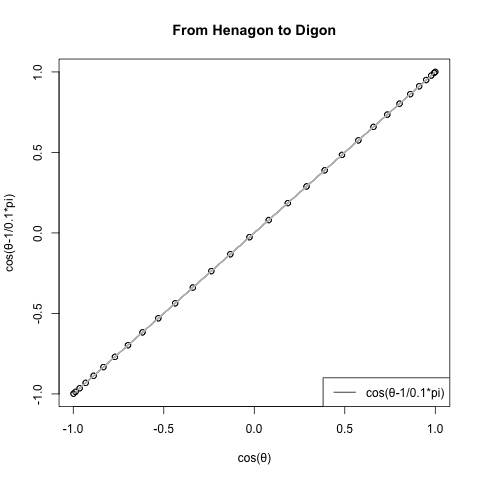
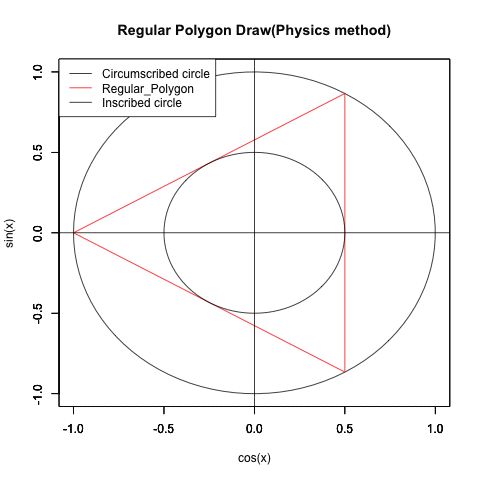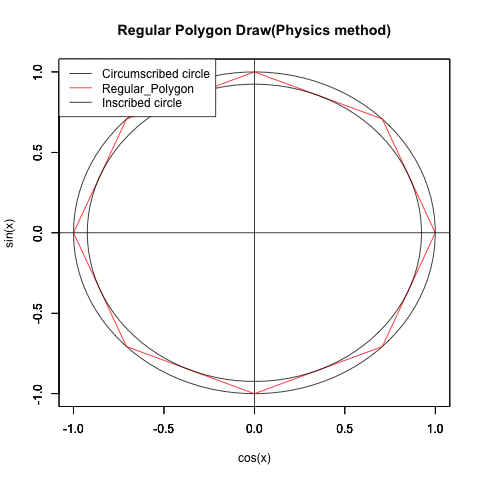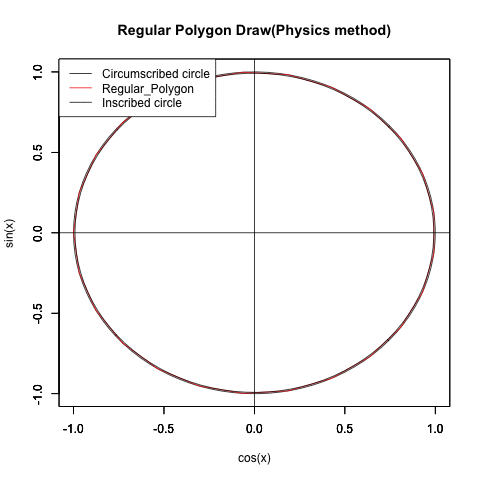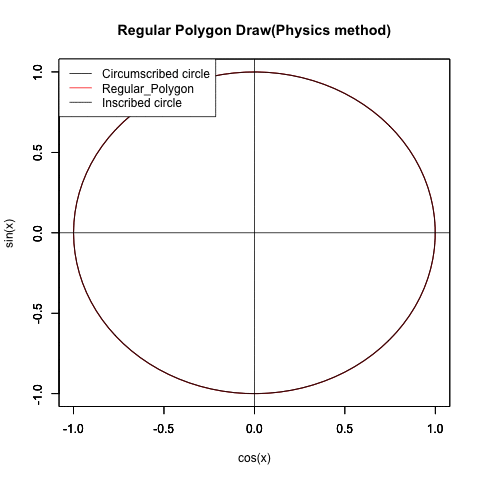
ところでこの図形、グルグル回せます。

①x+y(cos(θ)+sin(θ))…内接する正方形と外接する正方形の辺長比の最大は2の0.5乗すなわち{…1/2(2^-1),sqrt(2)/2(2^-0.5),1(2^0),sqrt(2)(2^0.5),2(2^1)…}の対数比に準拠して推移する。この時円周2πは4分割される。
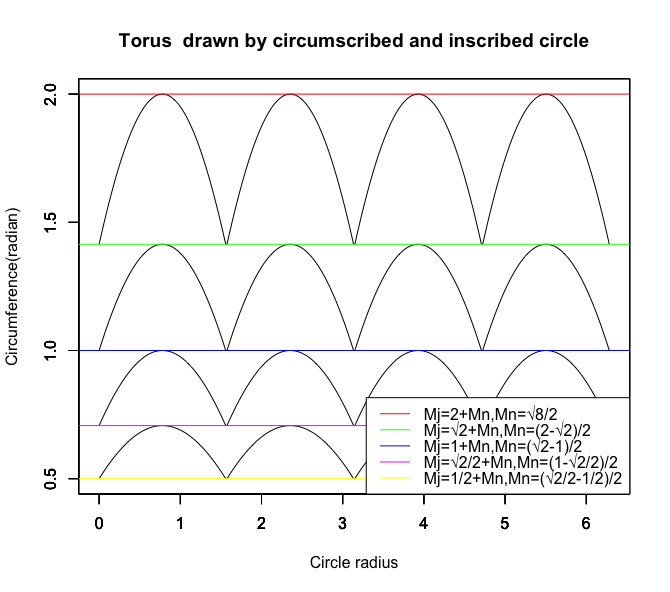
これは(正三角形同様に2の1乗の対数比で無限連鎖する)正方形の内接円と外接円の比率の推移に対応する(ちなみに正三角形の場合、円周2πは3分割される)。

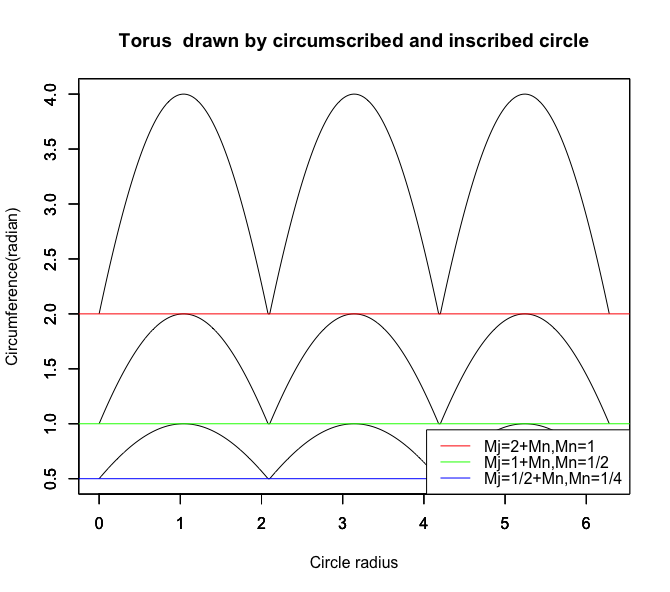
ちなみにx*y(cos(θ)*sin(θ))はx=y(cos(45度=1/4π)=sin(45度=1/4π))の時最大値0.5に。それぞれ1辺の長さはsqrt(2)/2(2乗して0.5=2^-1)となる。

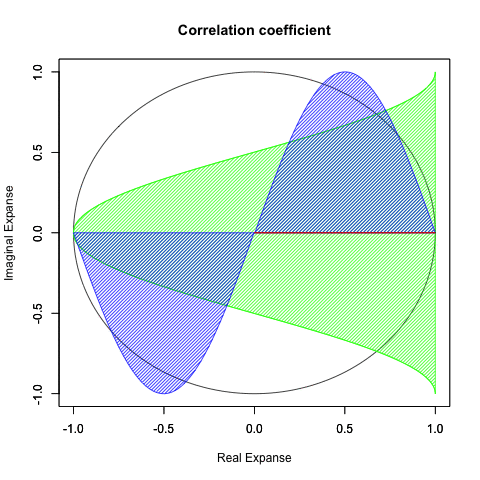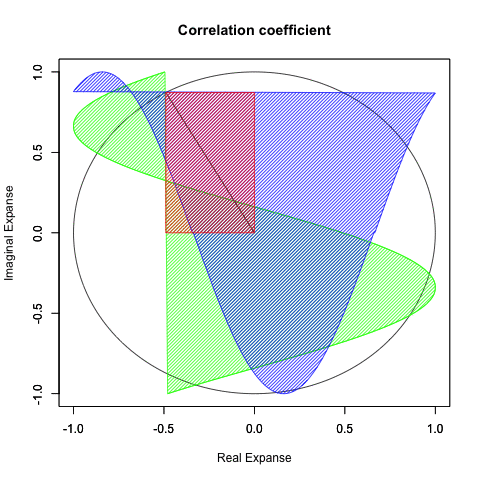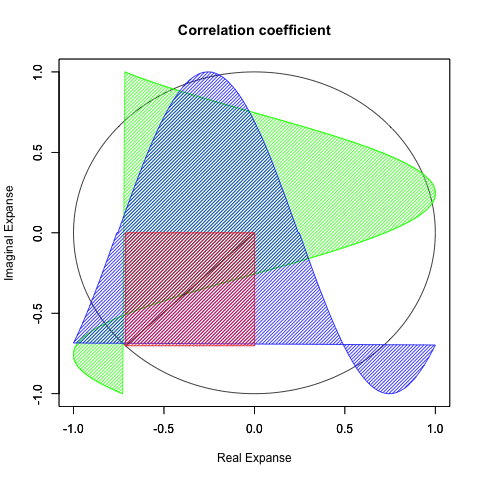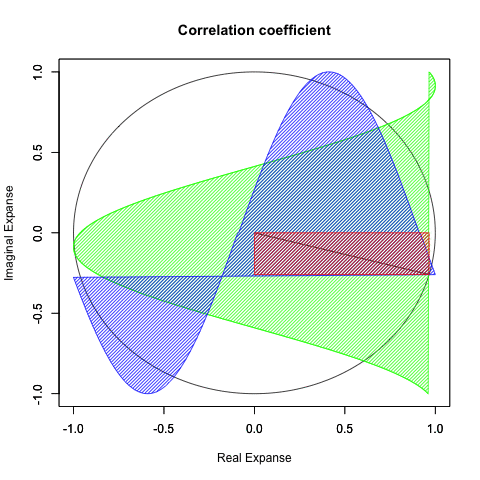
まとめると以下。
- cos(θ)+sin(θ)の最小値は1(cos(0)=1&sin(0)=0もしくはcos(π/2)=0&sin(π/2)=1)
- cos(θ)+sin(θ)の最大値は1+sqrt(2)(最小値+sqrt(2)/2*2)
- cos(θ)*sin(θ)の最小値は0(sin(0)=0もしくはcos(π/2)=0の時)
- cos(θ)*sin(θ)の最大値は0.5(sqrt(2)/2^2)
- cos(θ)^2+sin(θ)^2の結果は常に1(1+0~0.5+0.5~0+1)
要するに単位円上のcos(θ)とsin(θ)は以下の関係にある。
- cos(0)=1の時にsin(0)=0、sin(π/2)=1の時にcos(π/2)=0
- cos(π/4)=sin(π/4)=sqrt(2)/2*2。これは単位円に内接する正方形の1辺の長さ/2に対応する。
実はこれ、波形全体の1/4つまり第一象限においてのみ成立する特徴なのです。

ただしその回転アニメーションをみても分かる様に、立方体は周期全体を角数(Number of Corners)に合わせて1/4に分割した上で、その先頭部分だけを4回再生しているのみ。だから何の問題も生じないのです。


同様に正3角形(Equilateral triangle)は周期の先頭1/3を3回、正五角形(Regular pentagon)は周期の先頭1/5を5回繰り返してるのみ。

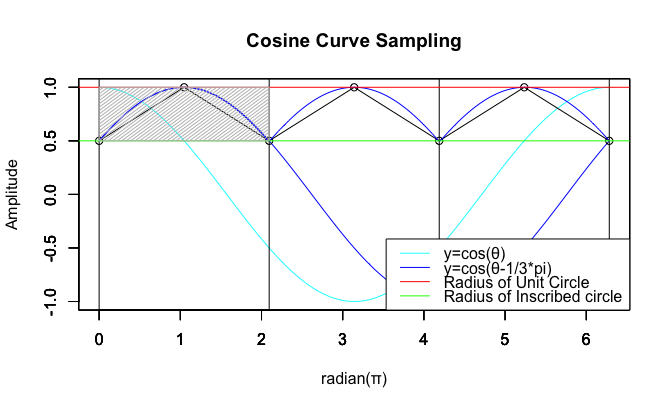


(調べてもそれらしい呼称が発見出来なかったので)とりあえずこの現象を「辺長サンプリング効果(Side length sampling effect)」と呼ぶ事にしたいと思います。多角形方程式(Poligons equattion)Cos(θ)+Cos(θ-π/NoC)i(ただしNoC=Number of Corners=角数)の結論に逆らって、正方形(Square)上においてオイラーの公式(Euler's formula)e^θi=cos(θ)+sin(θ)iが成立するのは、この現象のおかげとも。