正三角形(Equilateral triangle, 外角の大きさはpi/3=1.047198ラジアンあるいは180/pi=60度、内角の大きさは2*pi*(3-2)/3=2.094395あるいは180*(3-2)/3=60度)の場合

対象円に内接する正三角形の高さ(内接円の半径r*3)をh(height)とする。外接円の内接円に対する半径の比率は指数サイズ1すなわち対数比(...1/root^x,1/root,root/root,root,root^x...)で推移し平面充填性(同じ図面で平面を埋め尽くす能力)に加え空間充填性(同じ立体で空間を埋め尽くす能力)も備える。立体としては正四面体(Regular tetrahedron, 辺数6、頂点数4)を構成し、その表面積はsqrt(2)*a^2、体積はsqrt(2)/12*a^3で表される。正八面体(Regular octahedron, 辺数12、頂点数6、表面積2*sqrt(2)*a^2、体積sqrt(2)/3*a^3)や正二十面体(regular icosahedron、辺数30、頂点数12、表面積5*sqrt(2)*a^2、体積12/5*(3+sqrt(5))*a^3)とは双対の関係にある。
- 2*tan(pi/3)=3.464102
- 2*tan(pi/3)/cos(pi/3)=6.928203
- cos(pi/3)=1/2=0.5
一辺の長さがaの正3角形に内接する円の半径r
- r=a*(2*tan(pi/3))=a*3.464102
- a=r/(2*tan(pi/3))=r/3.464102
一辺の長さがaの正3角形に外接する円の半径R
- R=a/(2*tan(pi/3))/cos(pi/3)=a/6.928203
- a=R*(2*tan(pi/3))/cos(pi/3)=R*6.928203
一辺の長さがaの正3角形の外接円の半径と内接円の関係
- r=R*cos(pi/3)=R/2
- R=r/cos(pi/3)=2r
円周率近似計算の結果はなんと「7.348469<=π<=10.3923」で「不正解」範囲…
統計言語Rによる作表例
target_size<-c("3^-1","3^-1","3^-1","3^-1","3^0","3^0","3^0","3^0","3^1")
target_names<-c("3^-1(3^0r)","3^-1h=3^-1*3","3^-1a1=3^0a0","3^-1a1(3^0a0)*3","3^0(3^-1R,3^1r)","3^0h=3^0*3","3^0a1=3^1a0","3^0a1(3^1a0)*3","3^1(3^0R)")
target_values<-c("1/2=0.5","3/2=1.5","2*sqrt(1.5)=2.44949","6*sqrt(1.5)=7.348469","1.0","3.0","2*sqrt(3)=3.464102","6*sqrt(3)=10.3923","3.0")
Regula_falsi03<-data.frame(Target_size=target_size,Target_names=target_names,Target_values=target_values)
library(xtable)
print(xtable(Regula_falsi03), type = "html")
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 3^-1 | 3^-1(3^0r) | 1/2=0.5 |
| 2 | 3^-1 | 3^-1h=3^-1*3 | 3/2=1.5 |
| 3 | 3^-1 | 3^-1a1=3^0a0 | 2*sqrt(1.5)=2.44949 |
| 4 | 3^-1 | 3^-1a1(3^0a0)*3 | 6*sqrt(1.5)=7.348469 |
| 5 | 3^0 | 3^0(3^-1R,3^1r) | 1.0 |
| 6 | 3^0 | 3^0h=3^0*3 | 3.0 |
| 7 | 3^0 | 3^0a1=3^1a0 | 2*sqrt(3)=3.464102 |
| 8 | 3^0 | 3^0a1(3^1a0)*3 | 6*sqrt(3)=10.3923 |
| 9 | 3^1 | 3^1(3^0R) | 3.0 |
「1の原始冪根級数(One Primitive Sone series)」の一環としてζ^3に従う以下の三点は基本円(Basic circle,半径1,円周2π)に内接する正三角形を描く。
- 1
- (-1+sqrt(3)*(0+1i))/2
- (-1-sqrt(3)*(0+1i))/2
ちなみに(-1±sqrt(3)*(0+1i))/2はしばしば ω と書かれる。
統計言語Rによる立体図
#正三角形
library(rgl)
Rtime<-seq(0,2,length=4)
tr01<-c(1,(-1+sqrt(3)*(0+1i))/2,(-1-sqrt(3)*(0+1i))/2,1)
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test11")


基本円(Basic circle)上に同心円を描く任意の正三角形内で正三角形を回すと、その片長の比は2:2と1:2の間を反復し続ける。その比は多層化された内接円と外接円のサイズ比に等しい。
正三角形 統計言語Rによる実装例
Three_square_theorem03<-function(x){
c0<-c(0,2/3*pi,-2/3*pi,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("a","b","c",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[1]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x]), labels=c("ab","bc","ca"),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2))#塗りつぶし
polygon(c(c0_cos[1],line_scale_03_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_03_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))}
#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
Three_square_theorem03(i)
}
}, interval = 0.1, movie.name = "TEST003.gif")

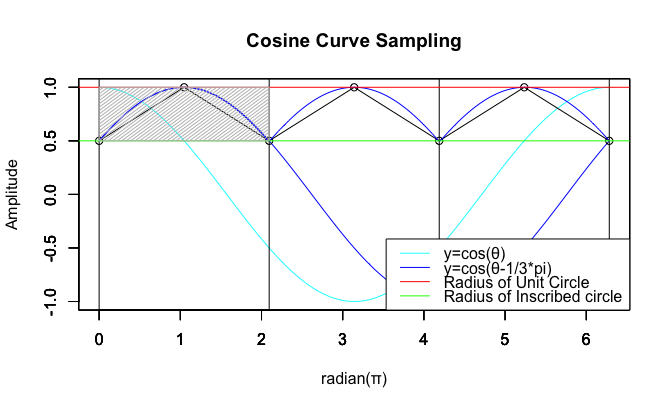
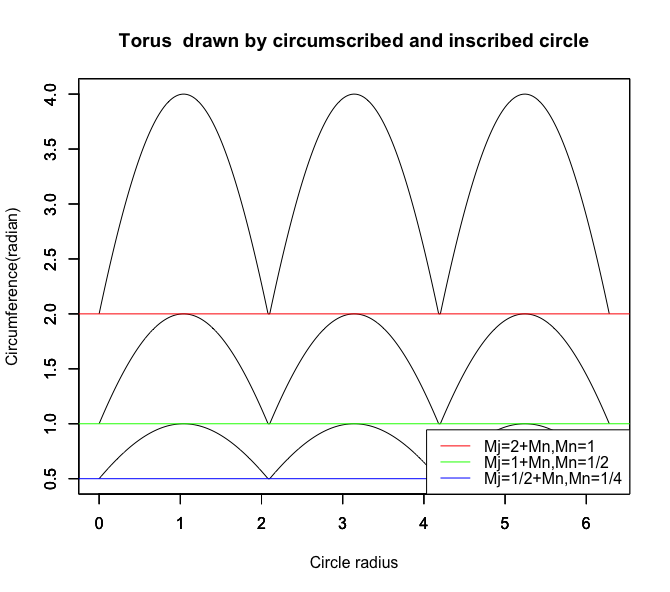
実はこれcos(2/3π-θ)と60度(-1/3pi)位相をズラした正弦波を120度(-2/3pi)単位で「サンプリング」して繰り返した内容。同心円単位で積層し、多層化されたトーラス(単torus, 複tori)を構築する。
正三角形 統計言語Rによる実装例(3進数)
Three_square_theorem03<-function(x){
c0<-c(0,2/3*pi,-2/3*pi,0)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",xlim=c(-1,1),ylim=c(-1,1),main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("00","01","02",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[1]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x]), labels=c("00-02","10-12","20-22"),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2))#塗りつぶし
polygon(c(c0_cos[1],line_scale_03_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_03_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))}
#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
Three_square_theorem03(i)
}
}, interval = 0.1, movie.name = "TEST003.gif")
