「正九角形(Regular pentagon、外角の大きさはpi/9=0.3490659ラジアンあるいは180/9=20度、内角の大きさは2*pi*(9-2)/9=4.886922ラジアンあるいは180*(9-2)/9=140度)」の場合

「1の原始冪根級数(One Primitive Sone series)」の一環としてζ^9の答えとなる9点は基本円(Basic circle,半径1,円周2π)に内接する正八角形を描く。
#現状、計算結果しか解らない。
Rtime<-seq(0,2,length=10)
tr01<-exp(seq(0,2*pi,length=10)*(0+1i))
tr01
- 1.0000000+0.0000000i
- 0.7660444+0.6427876i
- 0.1736482+0.9848078i
- -0.5000000+0.8660254i
- -0.9396926+0.3420201i
- -0.9396926-0.3420201i
- -0.5000000-0.8660254i
- 0.1736482-0.9848078i
- 0.7660444-0.6427876i
統計言語Rによる作図例
#正9角形
Rtime<-seq(0,2,length=10)
tr01<-exp(seq(0,2*pi,length=10)*(0+1i))
Real<-Re(tr01)
Imag<-Im(tr01)
#plot(Real,Imag,type="l")
plot3d(Real,Imag,Rtime,type="l",xlim=c(-1,1),ylim=c(-1,1),zlim=c(0,2))
movie3d(spin3d(axis=c(0,0,1),rpm=5),duration=10,fps=25,movie="~/Desktop/test09")


正九角形 統計言語Rによる実装例01
Three_square_theorem09<-function(x){
c0<-seq(0,2*pi,length=10)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("a","b","c","d","e","f","g","h","i",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[1]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x]), labels=c("ab","bc","cd","de","ef","fg","gh","hi","ia",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(2,2,2,2,2,2,2,2,2,2))#塗りつぶし
polygon(c(c0_cos[1],line_scale_09_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_09_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))}
#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
Three_square_theorem09(i)
}
}, interval = 0.1, movie.name = "TEST009.gif")

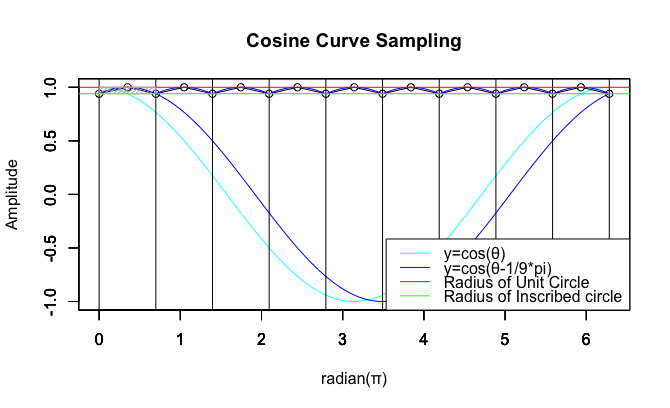
基本円(Basic circle)上に同心円を描く任意の正九形内で正九角形を回すと、その片長の比は1と内接円や外接円のサイズ比cos(pi/9)=0.9396926の間を反復し続ける。
正九角形 統計言語Rによる実装例(3進数)
Three_square_theorem09<-function(x){
c0<-seq(0,2*pi,length=10)
c0_cos<-cos(c0)
c0_sin<-sin(c0)
plot(c0_cos,c0_sin,type="l",main="Regular polygon rotation",xlab="Cos(θ)",ylab="Sin(θ)")
text(c0_cos,c0_sin, labels=c("000","010","020","100","110","120","200","210","220",""),col=c(rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0),rgb(1,0,0)),cex=c(2,2,2,2,2,2,2,2,2,2))
line_scale_01_cos<-seq(cos(c0[1]),cos(c0[2]),length=15)
line_scale_01_sin<-seq(sin(c0[1]),sin(c0[2]),length=15)
line_scale_02_cos<-seq(cos(c0[2]),cos(c0[3]),length=15)
line_scale_02_sin<-seq(sin(c0[2]),sin(c0[3]),length=15)
line_scale_03_cos<-seq(cos(c0[3]),cos(c0[4]),length=15)
line_scale_03_sin<-seq(sin(c0[3]),sin(c0[4]),length=15)
line_scale_04_cos<-seq(cos(c0[4]),cos(c0[5]),length=15)
line_scale_04_sin<-seq(sin(c0[4]),sin(c0[5]),length=15)
line_scale_05_cos<-seq(cos(c0[5]),cos(c0[6]),length=15)
line_scale_05_sin<-seq(sin(c0[5]),sin(c0[6]),length=15)
line_scale_06_cos<-seq(cos(c0[6]),cos(c0[7]),length=15)
line_scale_06_sin<-seq(sin(c0[6]),sin(c0[7]),length=15)
line_scale_07_cos<-seq(cos(c0[7]),cos(c0[8]),length=15)
line_scale_07_sin<-seq(sin(c0[7]),sin(c0[8]),length=15)
line_scale_08_cos<-seq(cos(c0[8]),cos(c0[9]),length=15)
line_scale_08_sin<-seq(sin(c0[8]),sin(c0[9]),length=15)
line_scale_09_cos<-seq(cos(c0[9]),cos(c0[1]),length=15)
line_scale_09_sin<-seq(sin(c0[9]),sin(c0[1]),length=15)
text(c(line_scale_01_cos[x],line_scale_02_cos[x],line_scale_03_cos[x],line_scale_04_cos[x],line_scale_05_cos[x],line_scale_06_cos[x],line_scale_07_cos[x],line_scale_08_cos[x],line_scale_09_cos[x]),c(line_scale_01_sin[x],line_scale_02_sin[x],line_scale_03_sin[x],line_scale_04_sin[x],line_scale_05_sin[x],line_scale_06_sin[x],line_scale_07_sin[x],line_scale_08_sin[x],line_scale_09_sin[x]), labels=c("000-002","010-012","020-022","100-102","110-112","120-122","200-202","210-212","220-222",""),col=c(rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1),rgb(0,0,1)),cex=c(1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5,1.5))#塗りつぶし
polygon(c(c0_cos[1],line_scale_09_cos[x],line_scale_01_cos[x],c0_cos[1]), #x
c(c0_sin[1],line_scale_09_sin[x],line_scale_01_sin[x],c0_sin[1]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[2],line_scale_01_cos[x],line_scale_02_cos[x],c0_cos[2]), #x
c(c0_sin[2],line_scale_01_sin[x],line_scale_02_sin[x],c0_sin[2]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[3],line_scale_02_cos[x],line_scale_03_cos[x],c0_cos[3]), #x
c(c0_sin[3],line_scale_02_sin[x],line_scale_03_sin[x],c0_sin[3]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[4],line_scale_03_cos[x],line_scale_04_cos[x],c0_cos[4]), #x
c(c0_sin[4],line_scale_03_sin[x],line_scale_04_sin[x],c0_sin[4]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[5],line_scale_04_cos[x],line_scale_05_cos[x],c0_cos[5]), #x
c(c0_sin[5],line_scale_04_sin[x],line_scale_05_sin[x],c0_sin[5]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[6],line_scale_05_cos[x],line_scale_06_cos[x],c0_cos[6]), #x
c(c0_sin[6],line_scale_05_sin[x],line_scale_06_sin[x],c0_sin[6]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[7],line_scale_06_cos[x],line_scale_07_cos[x],c0_cos[7]), #x
c(c0_sin[7],line_scale_06_sin[x],line_scale_07_sin[x],c0_sin[7]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))#塗りつぶし
polygon(c(c0_cos[8],line_scale_07_cos[x],line_scale_08_cos[x],c0_cos[8]), #x
c(c0_sin[8],line_scale_07_sin[x],line_scale_08_sin[x],c0_sin[8]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))
#塗りつぶし
polygon(c(c0_cos[9],line_scale_08_cos[x],line_scale_09_cos[x],c0_cos[9]), #x
c(c0_sin[9],line_scale_08_sin[x],line_scale_09_sin[x],c0_sin[9]), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=rgb(0,1,0))}
#アニメーション
library("animation")
Time_Code=c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)
saveGIF({
for (i in Time_Code){
Three_square_theorem09(i)
}
}, interval = 0.1, movie.name = "TEST009.gif")
