発端はこの記事。
数列の極限は,
- 1…(有限の値に)収束する。
- 2A…正の無限大に発散する。
- 2B…負の無限大に発散する。
- 3…振動する。
のいずれかである。2と3の場合をいずれも発散すると言う。
例題5「数列 An=(−1)^n の極限を調べよ」の解答
Anは−1 と 1 をひたすら交互に繰り返す。収束,正の無限大に発散,負の無限大に発散,のいずれにも当てはまらないので振動に分類される。

だが、本当に? とっさに脳裏に浮かんだはこういうイメージ。
- (-1)^-3=1/(-1*-1*-1)=-1
- (-1)^-2=1/(-1*-1)=1
- (-1)^-1=1/(-1)=-1
- (-1)^0=-1/(-1)=1
- (-1)^1=-1
- (-1)^2=-1*-1=1
- (-1)^3=-1*-1*-1=-1
どうやら計算上もこの考え方で合ってる様だ?
上記計算の検証例
#(-1)^-3
1/(-1*-1*-1)
[1] -1
#(-1)^-2
1/(-1*-1)
[1] 1
#(-1)^-1
1/(-1)
[1] -1
#(-1)^0
-1/(-1)
[1] 1
#(-1)^1
-1
[1] -1
#(-1)^2
-1*-1
[1] 1
#(-1)^3
-1*-1*-1
[1] -1
上掲データの統計言語Rによる作表・作図例
cx<-c(-3,-2,-1,0,1,2,3)
cy<-c(-1,1,-1,1,-1,1,-1)
Vibration <- data.frame(Period=cx, Amplitude=cy)#作表する
library(xtable)
print(xtable(Vibration),type = "html")
#作図する
plot(cx,cy,type="l",main="An=(−1)^n",xlab="X",ylab="Y=(−1)^X")
| Period | Amplitude | |
|---|---|---|
| 1 | -3.00 | -1.00 |
| 2 | -2.00 | 1.00 |
| 3 | -1.00 | -1.00 |
| 4 | 0.00 | 1.00 |
| 5 | 1.00 | -1.00 |
| 6 | 2.00 | 1.00 |
| 7 | 3.00 | -1.00 |

ところがコンピューターにこれをそのまま計算させようとすると、小数点下がうまく補完出来ず躓いてしまうのです。
上掲グラフの統計言語Rによるプログラミング例
cx<-seq(-3,3,length=61)
f0<-function(x){(-1)^x}
cy<-f0(cx)
Vibration <- data.frame(Period=cx, Amplitude=cy)#変数内のデータの直接表示
cy#作表する
library(xtable)
print(xtable(Vibration),type = "html")
cy

作表結果
| Period | Amplitude | |
|---|---|---|
| 1 | -3.00 | -1.00 |
| 2 | -2.90 | |
| 3 | -2.80 | |
| 4 | -2.70 | |
| 5 | -2.60 | |
| 6 | -2.50 | |
| 7 | -2.40 | |
| 8 | -2.30 | |
| 9 | -2.20 | |
| 10 | -2.10 | |
| 11 | -2.00 | 1.00 |
| 12 | -1.90 | |
| 13 | -1.80 | |
| 14 | -1.70 | |
| 15 | -1.60 | |
| 16 | -1.50 | |
| 17 | -1.40 | |
| 18 | -1.30 | |
| 19 | -1.20 | |
| 20 | -1.10 | |
| 21 | -1.00 | -1.00 |
| 22 | -0.90 | |
| 23 | -0.80 | |
| 24 | -0.70 | |
| 25 | -0.60 | |
| 26 | -0.50 | |
| 27 | -0.40 | |
| 28 | -0.30 | |
| 29 | -0.20 | |
| 30 | -0.10 | |
| 31 | 0.00 | 1.00 |
| 32 | 0.10 | |
| 33 | 0.20 | |
| 34 | 0.30 | |
| 35 | 0.40 | |
| 36 | 0.50 | |
| 37 | 0.60 | |
| 38 | 0.70 | |
| 39 | 0.80 | |
| 40 | 0.90 | |
| 41 | 1.00 | -1.00 |
| 42 | 1.10 | |
| 43 | 1.20 | |
| 44 | 1.30 | |
| 45 | 1.40 | |
| 46 | 1.50 | |
| 47 | 1.60 | |
| 48 | 1.70 | |
| 49 | 1.80 | |
| 50 | 1.90 | |
| 51 | 2.00 | 1.00 |
| 52 | 2.10 | |
| 53 | 2.20 | |
| 54 | 2.30 | |
| 55 | 2.40 | |
| 56 | 2.50 | |
| 57 | 2.60 | |
| 58 | 2.70 | |
| 59 | 2.80 | |
| 60 | 2.90 | |
| 61 | 3.00 | -1.00 |
ここで「虚数(Imaginary number)」や「複素数(complex number)」といった概念導入による「それまで(離散的な)整数としてしか扱えなかった数理を(連続的な)実数に拡張する」数理上のパラダイムシフトが必要となる訳ですね。
二乗すると-2となる虚数(Imaginary number)は現実に存在しない数なので、虚数を含む複素数a+biも現実には存在しない数です。この言葉を初めて書物で用いたのは「我思う、故に我あり」で有名なデカルトとされていますが、活用方法も思いつかず「想像上の数(Nombre Imaginaire)」と否定的ニュアンスでしか捉えてませんでした。
それから数百年間は「詭弁的な数字であり、実用性はない」「ただの想像上の数に過ぎない」と否定的に評価されていたそうですが、オイラーの等式で有名なレオンハルト・オイラーが虚数のもつ重要性を解き明かした後、その評価は一変。
さらに研究が進むにつれ、その存在を仮定して計算に使ってみたら非常に便利であることが分かり、数学者の間で広く使われるようになったようです。
統計言語Rによるプログラミング例
cx<-seq(-3,3,length=61)
f0<-function(x){(-1)^(x*(0+1i))}
cyr<-Re(f0(cx))
cyi<-Im(f0(cx))
#CA=Correct Answer
CA_cy<-Re(f0(cx*2))
#作表する
Vibration01 <- data.frame(Period=cx, Real=cyr,Imaginal=cyi,CA=CA_cy)
library(xtable)
print(xtable(Vibration01),type = "html")
#「実数」領域の作図
plot(Vibration$Period,Vibration$Real,type="l",ylim=c(-1,1),col=rgb(0,1,0),main="An=(−1)^n",xlab="X",ylab="Y=(−1)^X")
par(new=T)#上書き指定
#「虚数」領域の作図
plot(Vibration$Period,Vibration$Imaginal,type="l",ylim=c(-1,1),col=rgb(0,0,1),main="",xlab="",ylab="")par(new=T)#上書き指定
#正解領域の作図
plot(cx,CA_cy,type="l",ylim=c(-1,1),col=rgb(1,0,0),main="",xlab="",ylab="")#凡例
legend("topright", legend=c("Real number","Imaginaly number","Correct Answer"),lty=c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))
作表結果
| Period | Real | Imaginal | CA | |
|---|---|---|---|---|
| 1 | -3.00 | 0.00 | -1.00 | -1.00 |
| 2 | -2.90 | -0.16 | -0.99 | -0.95 |
| 3 | -2.80 | -0.31 | -0.95 | -0.81 |
| 4 | -2.70 | -0.45 | -0.89 | -0.59 |
| 5 | -2.60 | -0.59 | -0.81 | -0.31 |
| 6 | -2.50 | -0.71 | -0.71 | 0.00 |
| 7 | -2.40 | -0.81 | -0.59 | 0.31 |
| 8 | -2.30 | -0.89 | -0.45 | 0.59 |
| 9 | -2.20 | -0.95 | -0.31 | 0.81 |
| 10 | -2.10 | -0.99 | -0.16 | 0.95 |
| 11 | -2.00 | -1.00 | -0.00 | 1.00 |
| 12 | -1.90 | -0.99 | 0.16 | 0.95 |
| 13 | -1.80 | -0.95 | 0.31 | 0.81 |
| 14 | -1.70 | -0.89 | 0.45 | 0.59 |
| 15 | -1.60 | -0.81 | 0.59 | 0.31 |
| 16 | -1.50 | -0.71 | 0.71 | 0.00 |
| 17 | -1.40 | -0.59 | 0.81 | -0.31 |
| 18 | -1.30 | -0.45 | 0.89 | -0.59 |
| 19 | -1.20 | -0.31 | 0.95 | -0.81 |
| 20 | -1.10 | -0.16 | 0.99 | -0.95 |
| 21 | -1.00 | -0.00 | 1.00 | -1.00 |
| 22 | -0.90 | 0.16 | 0.99 | -0.95 |
| 23 | -0.80 | 0.31 | 0.95 | -0.81 |
| 24 | -0.70 | 0.45 | 0.89 | -0.59 |
| 25 | -0.60 | 0.59 | 0.81 | -0.31 |
| 26 | -0.50 | 0.71 | 0.71 | -0.00 |
| 27 | -0.40 | 0.81 | 0.59 | 0.31 |
| 28 | -0.30 | 0.89 | 0.45 | 0.59 |
| 29 | -0.20 | 0.95 | 0.31 | 0.81 |
| 30 | -0.10 | 0.99 | 0.16 | 0.95 |
| 31 | 0.00 | 1.00 | 0.00 | 1.00 |
| 32 | 0.10 | 0.99 | -0.16 | 0.95 |
| 33 | 0.20 | 0.95 | -0.31 | 0.81 |
| 34 | 0.30 | 0.89 | -0.45 | 0.59 |
| 35 | 0.40 | 0.81 | -0.59 | 0.31 |
| 36 | 0.50 | 0.71 | -0.71 | 0.00 |
| 37 | 0.60 | 0.59 | -0.81 | -0.31 |
| 38 | 0.70 | 0.45 | -0.89 | -0.59 |
| 39 | 0.80 | 0.31 | -0.95 | -0.81 |
| 40 | 0.90 | 0.16 | -0.99 | -0.95 |
| 41 | 1.00 | -0.00 | -1.00 | -1.00 |
| 42 | 1.10 | -0.16 | -0.99 | -0.95 |
| 43 | 1.20 | -0.31 | -0.95 | -0.81 |
| 44 | 1.30 | -0.45 | -0.89 | -0.59 |
| 45 | 1.40 | -0.59 | -0.81 | -0.31 |
| 46 | 1.50 | -0.71 | -0.71 | 0.00 |
| 47 | 1.60 | -0.81 | -0.59 | 0.31 |
| 48 | 1.70 | -0.89 | -0.45 | 0.59 |
| 49 | 1.80 | -0.95 | -0.31 | 0.81 |
| 50 | 1.90 | -0.99 | -0.16 | 0.95 |
| 51 | 2.00 | -1.00 | 0.00 | 1.00 |
| 52 | 2.10 | -0.99 | 0.16 | 0.95 |
| 53 | 2.20 | -0.95 | 0.31 | 0.81 |
| 54 | 2.30 | -0.89 | 0.45 | 0.59 |
| 55 | 2.40 | -0.81 | 0.59 | 0.31 |
| 56 | 2.50 | -0.71 | 0.71 | 0.00 |
| 57 | 2.60 | -0.59 | 0.81 | -0.31 |
| 58 | 2.70 | -0.45 | 0.89 | -0.59 |
| 59 | 2.80 | -0.31 | 0.95 | -0.81 |
| 60 | 2.90 | -0.16 | 0.99 | -0.95 |
| 61 | 3.00 | 0.00 | 1.00 | -1.00 |
作図結果

あぁ、こりゃもう完全にオイラーの公式(Euler's formula)cos(θ)+sin(θi)が成立して円とか描いちゃうパターンですわ。
*楕円とかもっと歪な形で現れると思いきや、あら不思議…どうして? まぁ別に、歪む要因も見当たらない訳ですが。
統計言語Rによるプログラミング例
cx<-seq(-3,3,length=61)
f0<-function(x){(-1i)^x}
cxr<-Re(f0(cx))
cyi<-Im(f0(cx))
#複素空間の作図
plot(cxr,cyi,asp=1,type="l",ylim=c(-1,1),col=rgb(1,0,0),main="An=(−1)^n",xlab="Real number",ylab="Imaginaly number")
#凡例
legend("topright", legend=c("Real+Imaginal*i"),lty=c(1),col=c(rgb(1,0,0)))

周期が倍だと円を2回描きます。
統計言語Rによるプログラミング例
cx<-seq(-3,3,length=61)
f0<-function(x){(-1i)^(2*x)}
cxr<-Re(f0(cx))
cyi<-Im(f0(cx))
#複素空間の作図
plot(cxr,cyi,asp=1,type="l",ylim=c(-1,1),col=rgb(1,0,0),main="An=(−1)^n",xlab="Real number",ylab="Imaginaly number")
#凡例
legend("topright", legend=c("Real+Imaginal*i"),lty=c(1),col=c(rgb(1,0,0)))

そしていよいよ、冒頭図の作画に。
統計言語Rによるプログラミング例
*赤が削除箇所と修正箇所
cx<-seq(-3,3,length=61)
f0<-function(x){(-1i)^x}
cyr<-Re(f0(cx))
cyi<-Im(f0(cx))
#CA=Correct Answer
CA_cy<-Re(f0(cx*2))
#作表する
#Vibration01 <- data.frame(Period=cx, Real=cyr,Imaginal=cyi,CA=CA_cy)
#library(xtable)
#print(xtable(Vibration01),type = "html")
#「実数」領域の作図
#plot(Vibration$Period,Vibration$Real,type="l",ylim=c(-1,1),col=rgb(0,1,0),main="An=(−1)^n",xlab="X",ylab="Y=−1i^2X")
#par(new=T)#上書き指定
#「虚数」領域の作図
#plot(Vibration$Period,Vibration$Imaginal,type="l",ylim=c(-1,1),col=rgb(0,0,1),main="",xlab="",ylab="")#par(new=T)#上書き指定
#正解領域の作図
plot(cx,CA_cy,type="l",ylim=c(-1,1),col=rgb(0,0,0),main="-1^θ=-1i^2^θ=-1i^2θ",xlab="X",ylab="Y=-1i^2X")#凡例
#legend("topright", legend=c("Real number","Imaginaly number","Correct Answer"),lty=c(1,1,1),col=c(rgb(0,1,0),rgb(0,0,1),rgb(1,0,0)))

「円を自然に回してみせるにはタイムラインと座標変換にSin波を射影すると良い」現象と何か関係ありそうですが、現段階ではよく分かりません…
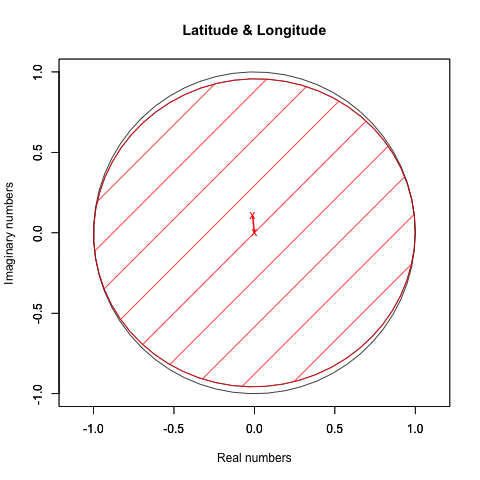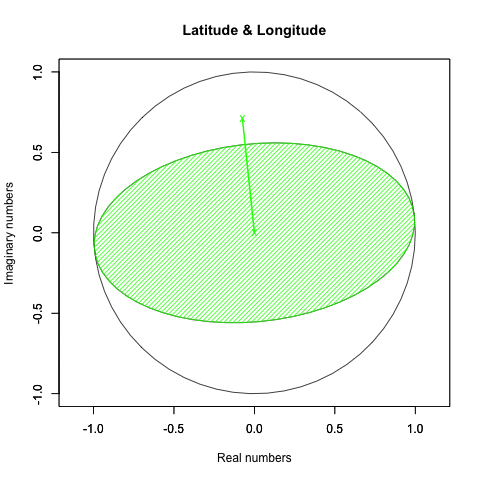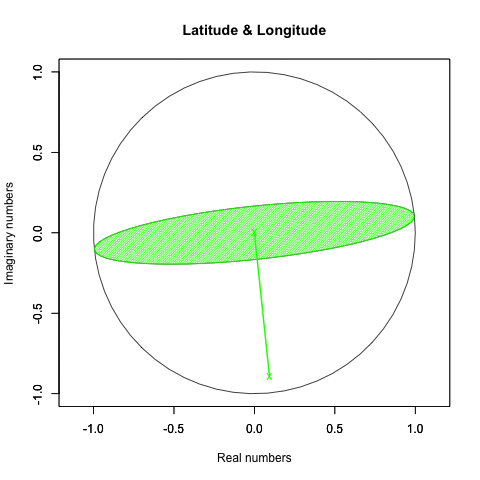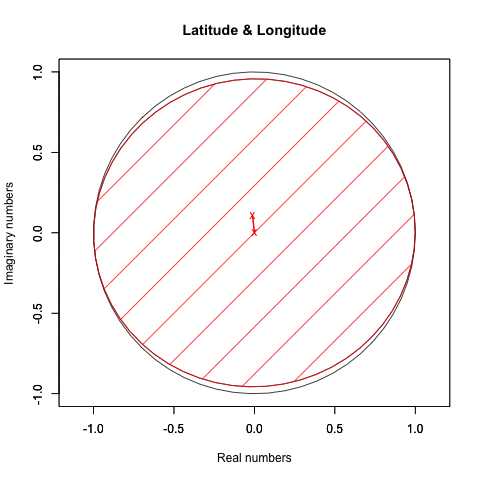
この一例だけ見ても「虚数や複素数は(実数域まで含む数理を扱う上で必ず必須になるとはいえない)思想実験屋が弄ぶ玩具に過ぎない」なる発想が間違っているのは明らか。むしろおそらく「(観察物理学者ならとっくの昔に気付いていた筈の、伝統的方法を継承して研鑽するだけでは克服不可能な)近世以前の数学の欠陥を補う重要な方便として近代数学以降に採用された」と考える方がよほ自然なのです。
回転運動を回転面上の観測者が真横から見ると物体は単振動しているように見える。あるいは、物体のx座標とy座標は互いに位相が90度=π/2ずれた単振動を行っている。
振動運動では回転速度のことを周波数または振動数と呼ぶ。
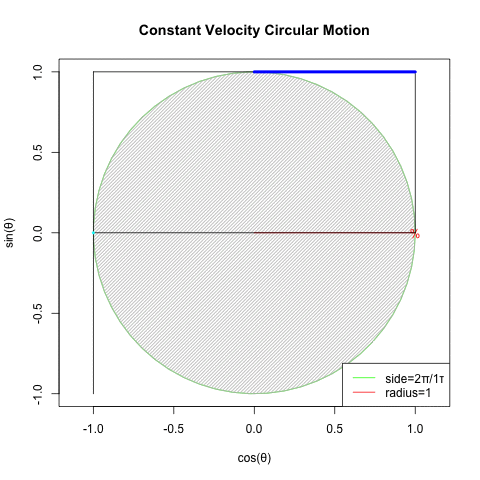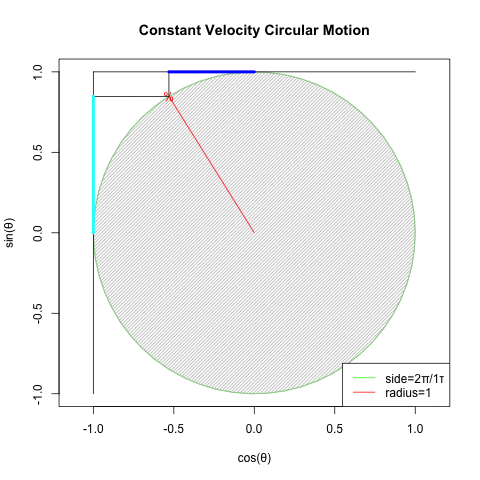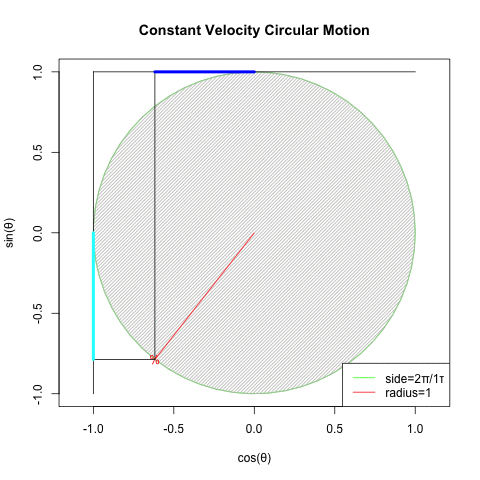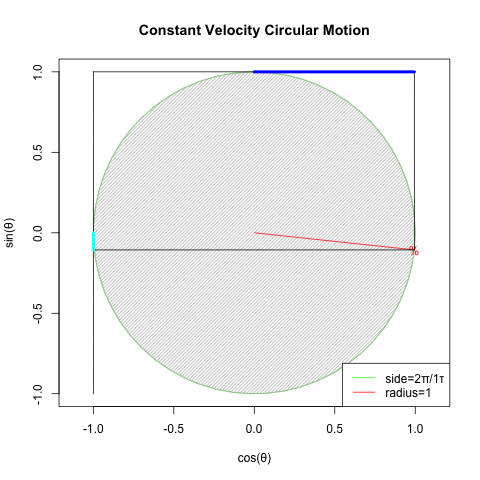
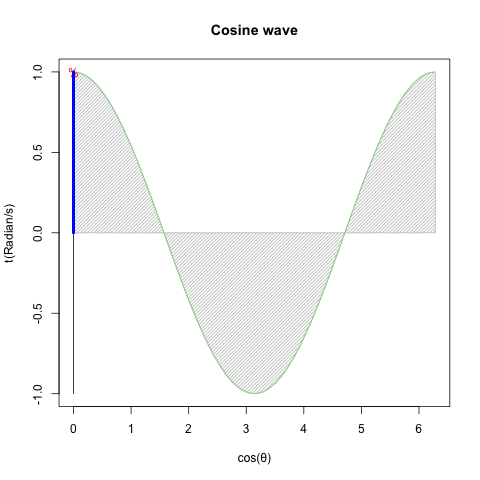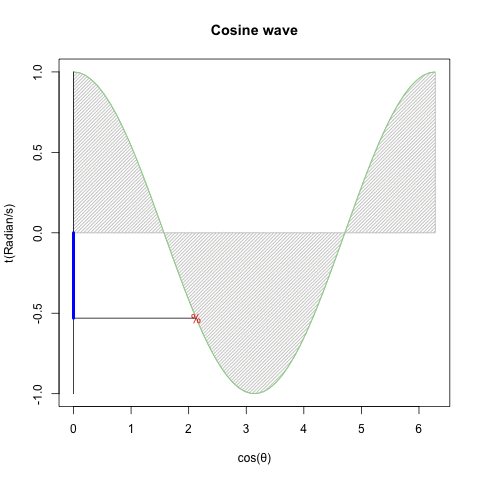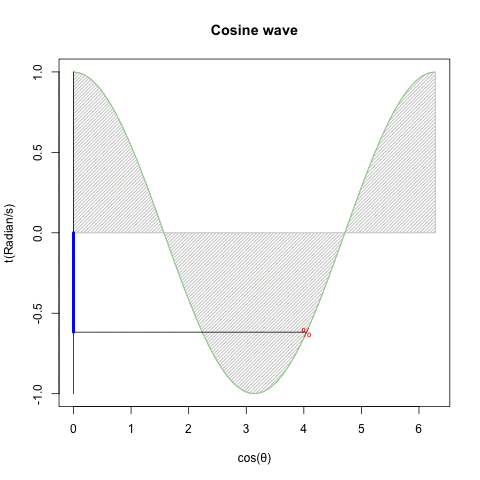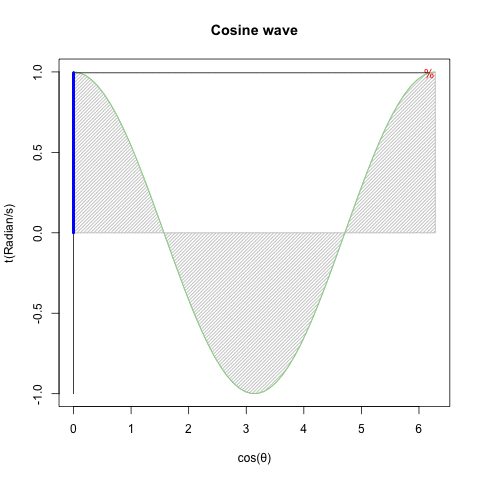

確かに手段は何であれ「X軸にCos波、Y軸にSin波」を配する事さえ思いつけば円は描けてしまうのです。とはいえ実際にはこうした振動観自体、オイラーの公式(Euler's formula)cos(θ)+sin(θi)がにインスパイアされて生まれたという話も。何れにせよ単振動(Simple Harmonic Oscillation)の研究史自体が「フックの法則(Hooke's law、ラテン語アナグラムによる「鍵付き」発表1676年、正解の発表1678年)」までしか遡れないので、現代人の感覚では誤差範囲に過ぎないという話も。