Yacas (ˈjækəs, やかす) - Wikipedia
GNU General Public License にしたがった利用と配布が認められているフリーソフトウェアの汎用計算機代数ソフトウェアで、名前は Yet Another Computer Algebra System から来ている。
計算機代数の演算を行うシステムであるため、数式の記号操作ができる。また記号計算および任意精度の数値計算を行うための独自のプログラミング言語処理系を備えている。多くの数式処理操作を実装したスクリプトのライブラリを持っており、新たに実装したアルゴリズムの追加が容易に行えるようになっている。スクリプト言語および実装されている機能とアルゴリズムについての文書が多数用意されている。
例えばこう使います。分母をそのまま残し、約分までしてくれる…
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
yacas("4/6")
expression(2/3)
#Rの計算結果
4/6
[1] 0.6666667
とはいえ、頻繁に利用されてる有用な箇所以外は色々とポンコツ?
高校数学の内容への挑戦
1956年の学習指導要領で登場。1947年度から1951年度の学習指導要領まで、高校1年生を対象とした数学の初歩的内容としては、会計などに関係しているような実務的な内容が多く一般教養の一環といった趣旨の強い「一般数学」と、将来数学を必要とする生徒、あるいは、数学をもっと深く学習したい生徒に対し、その必要と関心に基いて行われた「解析I」「幾何」に分かれていた。こうした仕分けを廃し、高校数学の基礎的内容を一本化して登場したのが数学Iという科目である。
1章 2次関数
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#Ryacasにおける関数の定義と典型的利用例
yacas("f001(x):= 2*x^2+1")
expression(TRUE)
yacas("f001(3)")
expression(19)
yacas("f001(a)")
expression(2 * a^2 + 1)
#Rにおける関数の定義と典型的利用例
f0<-function(x){2*x^2+1}
f0(3)
[1] 19
a<-c(1,2,3,4,5)
f0(a)
[1] 3 9 19 33 51#注意:Ryacasの関数はRからは使えない。
f001(3)
f001(3) でエラー: 関数 "f001" を見つけることができませんでした 。
RYacasのgnuplotを使ったグラフ描画は省略(コマンドライン経由の連携なので上手く動かすのが難しい)。この単元では傾きの変化を見る為に以下の関数を扱います。
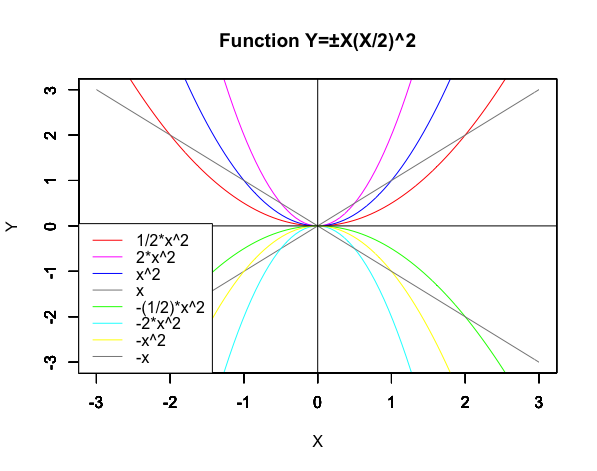
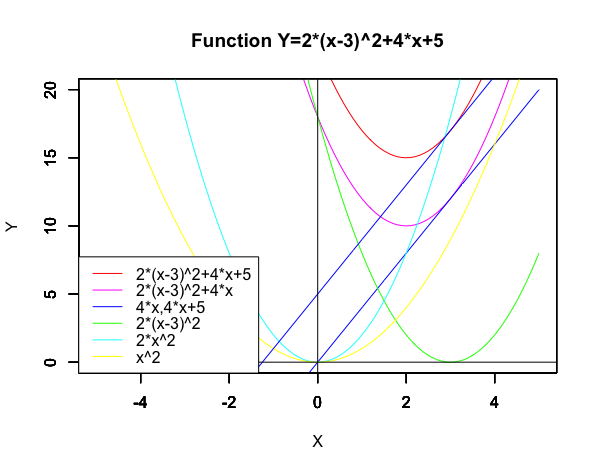
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#2次方程式の解の公式yacas("Solve(a*(x-b)^2+c*x+d,x) ")
Yacas vector:
[1] x == (root*2, 2) - (a * (-2 * b) + c))/(2 * a)
[2] x == -(a * (-2 * b) + c + root*3, 2))/(2 * a)
yacas("PSolve(a*(x-b)^2+c*x+d,x) ")
Yacas vector:
[1] (root*4, 2) - (a * (-2 * b) + c))/(2 * a)
[2] -(a * (-2 * b) + c + root*5, 2))/(2 * a)
yacas("PSolve(2*(x-3)^2+4*x+5,x) ")
Yacas vector:
[1] complex_cartesian(2, root(15/2, 2)) complex_cartesian(2, -root(120, 2)/4)
#Rによる計算結果>
a<-2; b<--3; c<-4; d<-5
(sqrt*6/(2 * a)
[1] -1.87868
-(a * (-2 * b) + c + sqrt*7/(2 * a)sqrt(15/2)[1] 2.738613sqrt(120)/4[1] 2.738613*計算が合ってない気がするがさて置く 統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例 library(Ryacas)#円関数yacas("Solve(Sqrt(x^2+y^2)-1,y)")Yacas vector:[1] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos(argument(1 - x^2)/2), sin(argument(1 - x^2)/2">*1
[2] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos*2
2章 三角比
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#三角比
yacas("TrigSimpCombine(Sin(a)^2+Cos(a)^2)")
expression(1)
yacas("Sin(a)/Cos(a)")
expression(tan(a))
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#円関数
yacas("Solve(Sqrt(x^2+y^2)-1,y)")
Yacas vector:
[1] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos(argument(1 - x^2)/2), sin(argument(1 - x^2)/2))
[2] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos*3
3章 個数の処理
階乗(factorial)
組み合わせの数やポアソン分布など、確率にまつわる様々な場面で登場する数。数学において非負整数 n のそれは1 から n までのすべての整数の積と定義されている。ちなみに0!=1。
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
yacas("5!")
expression(120)
#Rではガンマ関数を使ってn! = gamma(n+1)と計算する。さらに同じ計算をするfactorial(n)も追加された。
n<-5
gamma(n+1)
[1] 120
factorial(n)
[1] 120#大きな数の階乗を求めようとするとエラーが出る。Rでは階乗を計算するときに、Γ函数と呼ばれる函数を用いているのだが、このエラーは、あまりにも数が大きすぎてΓ函数の計算範囲を超えていることを示している。
factorial(171)
[1] Inf
警告メッセージ:
factorial(171) で: 'gammafn' 中の値が範囲を超えています#yacasもほぼ同じ反応だが警告なし。
yacas("171!")
expression(Inf)
順列(英sequence without repetition、仏arrangement、nPr=n!/(n-r)!)
異なるn個の中から異なるr個を取り出して1列に並べる数の事。記号Pで表す。例えば5人(A、B、C、D、E)の中から2人を並べる場合を考えると並べ方はAB、BA、AC、CA、DE、EDで合計は20通りになる。ABとBAを違うものとして考えるのがポイント。
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#nPr=n!/(n-r)!
yacas("(5!)/*4")
expression(4 * x^3 - 4 * x^2 + 3 * x - 9)
#乗法公式Ⅰ(中学数学範囲)…(x+a)*(x+b)と(a*x+b)*(c*x+d)、(a+b)^2と(a-b)^2の解法は本質的に同じだが,両方覚えておいて機械的に計算できる方が若干早いとも。
yacas("Expand*5")
expression(x^2 + (a + b) * x + b * a)
yacas("Expand*6")
expression(a^2 - b^2)
yacas("Expand*7")
expression*8")
expression(a^3 + b^3)
yacas("Expand*9")
expression(a^3 - b^3)
yacas("Expand*10#大学受験レベルの乗法公式。二項定理で計算してもよいが,4 乗の展開公式までは一瞬で言えるようにしておいた方がよいとされる。
yacas("Expand*11")
expression*12
#数学的に無意味な上に指数規則的にも無意味?パスカルの三角形(1)yacas("Expand*13")
expression(x^3 + x^2*y - x*y^2-y^3)
yacas("Expand*14")
expression(a^4 + 2 * (b * a^3) - 2 * (b^3 * a) - b^4)
*五乗
yacas("Expand*15")
expression(a^6 + 4 * (b * a^5) + 5 * (b^2 * a^4) - 5 * (b^4 *
a^2) - 4 * (b^5 * a) - b^6)
#その他の重要公式
yacas("Expand*16")
expression(x^3 + (a + (b + c)) * x^2 + *17")
#答えがa3+b3+c3−3abcとなる極めて重要な因数分解公式(3つの立方和)だがyacasは解かない。
yacas("Expand(a*(b^2-c^2)+b*(c^2-a^2)+c*(a^2-b^2))")
expression*18#あれ?テストでは(a-b)*(b-c)*(c-a)が答えとして要求されるみたいだけど?
#そして乗法公式
yacas("Expand*19")
expression*20
yacas("Expand*21
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#Factorは次数が1の場合のみ因数分解できる。
yacas("Factor(9*x^2+12*x+4)")
expression(9 * (x + 2/3)^2)
yacas("Factor(a^2+7*a+12)")
expression*22
整式の除法
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#商はDiv
yacas("Div(2*x^3-x^2-x+5,x^2-2*x+2)")
expression(2 * x + 3)
yacas("Div(2*x^3-x^2-x+5,x^2-2*x+2)")
yacas("Mod(2*x^3-x^2-x+5,x^2-2*x+2)")
#余りはMod
yacas("Mod(2*x^3-x^2-x+5,x^2-2*x+2)")
expression(x - 1)
平方根と立方根
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#Ryacasの計算結果(というかほとんど自動で計算してくれない)
yacas("Scrt(2)")
expression(Scrt(2))
yacas("2^0.5")
expression(2^0.5)
yacas("Root(2,2)")
expression(Root(2, 2))
yacas("Scrt(4)")
expression(Scrt(4))
yacas("Root(4)")
expression(Root(4))
yacas("Scrt(8)")
expression(Scrt(8))
yacas("Root(8)")
expression(Root(8))
yacas("2^(1/3)")
expression(2^(1/3))
yacas("Root(2,3)")
expression(Root(2, 3))
Rでの計算結果
sqrt(2)#平方根
[1] 1.414214
2^0.5
[1] 1.414214
sqrt(4)
[1] 2
sqrt(8)
[1] 2.8284272^(1/3)#立方根
[1] 1.259921
2章 数列
第1項がaで,公差がdであるような等差数列の第n項anはan=a+(n-1)d ,第1項がa,公比がrの等比数列の第n項anはan=a*r^(n-1)で表わされる。このように数列の第n項をnに関する式で表わせば,n に順次 1,2,3,… と数値を与えることにより,その数列のすべての項が得られ,数列が定まる。このように,第 n 項が n に関する式で記述されているとき,これを一般項という。二項定理による (a+b)^n=ΣnCr,a^(n-r)b^r の展開式において nCr,a^(n-r)b^r をその一般項ということがある。
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#一般項4n-1の数列を第1項から第5項まで。 最後の1は間隔。
yacas("Table(4*i-1,i,1,5,1)")
Yacas vector:
[1] 3 7 11 15 19
#1から50までの奇数。間隔は2。
yacas("Table(i,i,1,50,2)")
Yacas vector:
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
#数列の合計(一般項4n-1の第1項から第10項までの合計)
yacas("Sum(i,1,10,4*i-1) ")
expression(210)
統計言語Rでの同等の機能実現
#一般項4n-1の数列を第1項から第5項まで。 最後の1は間隔。
f00<-function(x){4*x-1}
d00<-seq(1,5,1)#c(1:5)でも良い
f00(d00)
[1] 3 7 11 15 19
#数列の合計(一般項4n-1の第1項から第10項までの合計)
f00<-function(x){4*x-1}
sum(f00(seq(1,10,1)))
[1] 210#1から50までの奇数。間隔は2。
seq(1,50,2)
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
#ついでに1以上50以下の奇数(2n+1)の「正しい」求め方
f11<-function(x){2*x+1}
d11<-seq(0,50,1)#ここでの50は「使われる可能性のある計算結果の上限」
d11
[1] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
[31] 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
d12<-f11(d11)
d12
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43
[23] 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 81 83 85 87
[45] 89 91 93 95 97 99 101
d12[0<d12& d12<50]
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49
#ついでに1以上50以下の偶数(2n)の「正しい」求め方
f21<-function(x){2*x}
d21<-seq(0,50,1)#ここでの50は「使われる可能性のある計算結果の上限」
d21
[1] 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
[31] 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
d22<-f21(d21)
d22
[1] 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42
[23] 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86
[45] 88 90 92 94 96 98 100
d22[0<d22& d22<50]
[1] 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48
ゼロは偶数である。このことを数学的に証明することは簡単であり、それを理解することも容易である。ゼロが偶数であることを証明するもっとも簡単な方法は、それが「偶数」の定義(2の倍数である整数)に当てはまることを確認することである。すなわち0=0×2である。結果的に、ゼロは偶数の特徴であるような性質をすべて持っている。例えば、0は2で割りきれる。0の両隣は奇数である、0はある整数(0)とそれ自身との和である。0要素の集合(空集合)は、二つの等しい集合に分割できる、等々。ゼロは、他の偶数が満たすべきパターンにもまた合致している。例えば、偶数-偶数=偶数のような算術における規則は、0が偶数であることを要求する。
しかしながら、一般社会において、ゼロの偶奇性を認識することは、他の整数の偶奇性に比較して困難が伴い、混乱の元になるようだ。ある研究によれば、小学校の生徒たちは半数程度がゼロが偶数であることを正しく認識できなかった。また、数学専攻の学生や数学の教師でさえ、0が偶数であることに対して、しばしば誤った認識を持つ。反応時間試験において、大部分の人々は、0が偶数と認識するのに要する時間は、2,4,6,8などより明らかに遅かった。
1956年の学習指導要領で登場。高等学校数学の初歩的内容から発展させていくものとしてはそれまで「解析II」という科目があった。しかし、「解析II」で扱う内容は、現在の数学IIと数学IIIの両方に大体相当する内容とさらに確率・統計内容を含むかなり広いものであった。一方でベクトルがなく、線形代数学に関する内容が少ないという問題があった。
こうしたことを受けて1956年度の学習指導要領では、高校数学の履修内容を段階化することと、発展的な内容を学習できるようにするために数学I、数学II、数学IIIという科目を設置したのである。
1章 図形と式
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#絶対値
yacas("Abs(x)")
expression(abs(x))
#三角関数の加法定理はできない。
#2倍角の公式もできない。
#積を和や差に変形する公式はできる。
#逆の公式はできない。
yacas("TrigSimpCombine(Sin(a)*Cos(b))")
expression(sin(b + a)/2 - sin(b - a)/2)
2章 数列と関数の極限
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
yacas("Limit(x,Infinity) (x^2+x+1)/(2*x^2+1)")
expression(1/2)
yacas("Limit(x,0) Sin(x)/x")
expression(1)
yacas("Limit(x,0) (1-Cos(x))/x^2")
expression(1/2)
3章 指数・対数関数
*正直この方面はYacasの得意分野ではなさそう。
3章 微分法
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#以下の様な連続計算も可能
yacas("f1(x) := 2*x+3")
expression(TRUE)
yacas("f2(x) := 2*x^2+3*x-1")
expression(TRUE)
yacas("D(x) f1(x)*f2(x)")
expression*23
yacas("Simplify(%)")
expression(12 * x^2 + 24 * x + 7)
#その他いろいろ
yacas("Simplify(%)")
expression(12 * x^2 + 24 * x + 7)
yacas("D(x) 1/(2*x+1) ")
expression(-2/(2 * x + 1)^2)
yacas("D(x) (3*x-1)/(x^2+1)")
expression*24/(x^2 + 1)^2)
yacas("Simplify(%)")
expression*25
yacas("D(x) (2*x^3-1)^4")
expression(24 * (x^2 * (2 * x^3 - 1)^3))
yacas("Simplify(%)")
expression(24 * (8 * x^11 - 12 * x^8 + 6 * x^5 - x^2))
yacas("D(x) Tan(x)")
expression(1/cos(x)^2)
yacas("D(x) Ln(x)")
expression(1/x)
yacas("D(x) a^x")
expression(a^x * log(a))
yacas("Exp(x)")
expression(exp(x))
#高次導関数
yacas("Simplify(D(x,2) Exp(x)*Sin(x))")
expression(2 * (exp(x) * cos(x)))
#Simplifyしないとこう。
yacas("D(x,2) Exp(x)*Sin(x)")
expression(exp(x) * cos(x) - exp(x) * sin(x) + (exp(x) * cos(x) +
exp(x) * sin(x)))
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
yacas("D(x) x^n")
expression(n * x^(n - 1))
yacas("D(x) x^3-3*x^2+4*x-2")
expression(3 * x^2 - 6 * x + 4)
yacas("Integrate(x) x^n")
expression(x^(n + 1)/(n + 1))
#定積分
yacas("Integrate(x,x1,x2) Cos(x)")
expression(sin(x2) - sin(x1))
yacas("Integrate(x,0,2) Abs(x-1)")
expression(1)
5章 積分法
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#色々な積分
yacas("Integrate(x) x^a")
expression(x^(a + 1)/(a + 1))
yacas("Integrate(x) 1/x")
expression(log(x))
yacas("Integrate(x) 1/Cos(x)^2")
expression(tan(x))
yacas("Integrate(x) a^x")
expression(a^x/log(a))
日本の高等学校における数学の科目の一つである。現行学習指導要領下での本科目は2012年度より学年進行で実施されている。
1994年4月施行…数学Iを履修した後に履修させ、4項目中2項目以上を選択履修させることとされた。
複素数と複素数平面ベクトル
確率分布(数学II、確率・統計)
- 確率の計算:条件付き確率、確率の乗法定理、事象の独立・従属
- 確率分布:確率変数と確率分布、確率変数の平均・分散・標準偏差、二項分布
算法とコンピュータ(数学II)
- コンピュータの機能、いろいろな算法のプログラム
2003年4月施行…原則として数学Iを履修した後に履修させ、4項目中2項目以上を選択履修させることとされた。
- 数列(数学A)
数列とその和:等差数列、等比数列、数列{n2}、階差数列など
漸化式と数学的帰納法:隣接2項間の漸化式、数学的帰納法- ベクトル(数学B)
平面上のベクトル:ベクトルとその演算、ベクトルの成分、ベクトルの内積、ベクトルの応用
空間座標とベクトル:空間座標、空間におけるベクトル- 統計とコンピュータ
資料の整理:度数分布表(小6、中2)、散布図(中2)
資料の分析:代表値(中2)、分散、標準偏差、相関係数(数学C)- 数値計算とコンピュータ(数学A、数学B、数学C)
簡単なプログラムいろいろなアルゴリズム:整数の計算、近似値の計算2012年4月施行…原則として数学Iを履修した後に履修させ、3項目中2項目以上を選択履修させることとされている。
数列(数学B)…数列とその和:等差数列、等比数列、数列{n2}、階差数列漸化式と数学的帰納法:隣接2項間の漸化式、数学的帰納法
ベクトル(数学B)…平面上のベクトル:ベクトルとその演算、ベクトルの成分、ベクトルの内積、ベクトルの応用空間座標とベクトル:空間座標、空間におけるベクトル
確率分布と統計的な推測(数学C)…確率分布:確率変数と確率分布、確率変数の平均・分散・標準偏差、二項分布、正規分布統計的な推測:母集団と標本、統計的な推測の考え(推定、検定)
1章ベクトル
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#内積の計算
yacas("{a,b,c}.{d,e,f}")
expression(a * d + b * e + c * f)
2章 複素数と複素数平面
*正直この方面はYacasの得意分野ではなさそう。
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#ド・モアブルの定理
yacas("(1+Sqrt(3)*I)^6")
expression(64)
yacas("(1+Sqrt(3)*I)^6")
高次方程式
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
yacas("PSolve(x^3-1,x)")
yacas vector:
[1] 1 complex_cartesian(-1/2, root(3/4, 2))
[3] complex_cartesian(-1/2, -root(3/4, 2))
yacas("PSolve(x^3-1==0,x)")
expression(PSolve(MakeUni(x^3 - 1 == 0, x)))
#本来は{1,Complex*3,Complex*4}とか表示される筈?
日本の高等学校における数学の科目の一つである。2012年度入学生から適用の現行学習指導要領下では他科目への統廃合が行われたため、本科目は廃止された。なお、学年進行のため、2011年度までの入学生に対し、全日制高校では2013年度まで授業が実施された。
1994年4月施行…数学Iを履修した後に履修させ、4項目中2項目以上を選択履修させることとされた。ほとんどの学校で、1と2が選択された。数学Cの科目を範囲とする大学の多くでは1と2を試験範囲とした。
行列(代数・幾何)
- 行列とその演算:和、差、実数倍、積、逆行列
- 連立1次方程式:行列による表現、消去法による解法
平面上の曲線(代数・幾何)
数値計算(新規)
- 方程式の近似解
- 数値積分法:区分求積法、面積の近似計算
統計処理(数学II、確率・統計)
- 資料の整理:代表値、散布度、相関
- 統計的な推測:正規分布、母集団と標本、推定
2003年4月施行…原則として数学I及び数学Aを履修した後に履修させ、4項目中2項目以上を選択履修させることとされた。主に高等教育で自然科学・社会科学を学ぶことを希望する者が履修するのが望ましいとされた科目である。実際普通科の理系では履修させる学校が多かった。多くの理系学部において入試でも出題範囲として出題された。一方で看護・医療系学部、薬学部の一部、農学部の一部などで出題範囲から外される大学もあった。そのため、高等学校で理系であっても数学Cを選択しない選択が出来るようになっていた。
行列
- 行列とその演算:和、差、実数倍、積、逆行列(数学C)
- 行列の応用:連立1次方程式(数学C)、点の移動(復活)
平面上の曲線(数学C)
確率分布(数学B)
- 確率の計算:条件付き確率、確率の乗法定理、事象の独立・従属
- 確率分布:確率変数と確率分布、確率変数の平均・分散・標準偏差、二項分布
統計処理(数学C)
- 正規分布、母集団と標本、推定
2012年4月施行…内容の取扱いは以下。
- 平面上の曲線が数学IIIに移行。
- 確率分布(条件付き確率を除く)と統計処理は数学Bに移行。条件付き確率は数学Aに移行。
- 行列は新科目「数学活用」で引用されるだけになり、普通科での履修科目から事実上消滅する。理数科向け理数科目「理数数学特論」では、行列は単元として残るが実際には理数科でもほとんど履修されてない。履修していた内容は大学における「線形代数」で履修することが多くなった。
かくして「線形代数」が選択科目から外されていったという次第。
1章 行列と線形計算
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#直線の公式(ただしb≠0)
yacas("Solve(a*x+b*y == c,y)")
Yacas vector:
[1] y == -*26
yacas("Identity(3)")
Yacas matrix:
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 1
#行列の累乗(MatrixPower(matrix,n))
yacas("MatrixPower({{1,-3},{1,-2}},4) ")
Yacas matrix:
[,1] [,2]
[1,] 1 -3
[2,] 1 -2
#逆行列(Inverse(matrix))
yacas("Inverse({{a,b},{c,d}}) ")
Yacas matrix:
[,1] [,2]
[1,] 1/a + c * b/(a^2 * (d - b * c/a)) -(b/a)/(d - b * c/a)
[2,] -(c/a)/(d - b * c/a) 1/(d - b * c/a)
#連立1次方程式の解法(SolveMatrix(matrix, vector) )
yacas("SolveMatrix({{1,2},{3,4}},{5,6})")
Yacas vector:
[1] -4 9/2
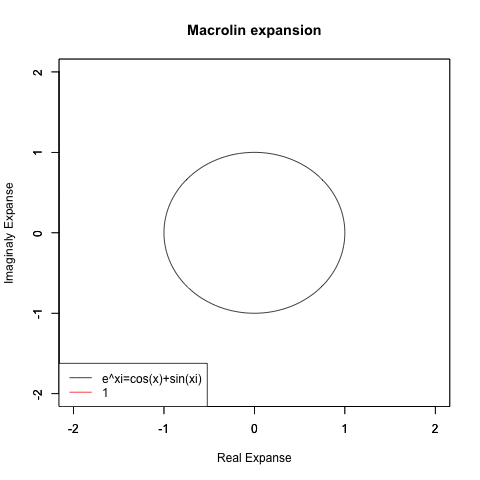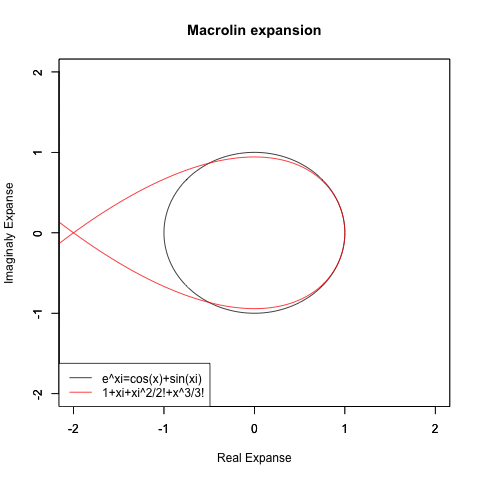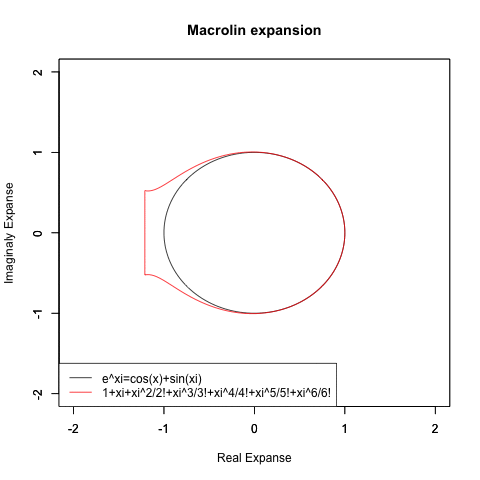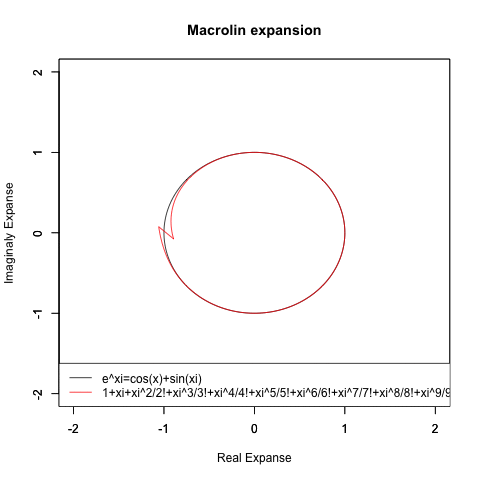
【追記】マクローリン展開
統計言語Rによる「オイラーの公式」の検証例
#まずは統計言語Rから呼べるYacasライブラリを導入
library(Ryacas)
#コサイン関数Cos(x)=x/1! - x^2/2! + x^4/4! - x^6/6! + x^8/8!...
yacas("Taylor(x, 0, 8) Cos(x)") #マクローリン展開
expression(1 - x^2/2 + x^4/24 - x^6/720 + x^8/40320)
#サイン関数sin(x)=x/1! - x^3/3! + x^5/5! - x^7/7! + x^9/9!...
yacas("Taylor(x, 0, 11) Sin(x)") #マクローリン展開
expression(x - x^3/6 + x^5/120 - x^7/5040 + x^9/362880それぞれ自然対数eのマクローリン展開の一部っぽい。
#自然対数Exp(x)=x/1! + x^2/2! + x^3/3! + x^4/4! + x^4/5! + x^6/6! + x^7/7! + x^8/8! + x^9/9!...
yacas("Taylor(x, 0, 9) Exp(x)") #マクローリン展開
expression(x + x^2/2 + x^3/6 + x^4/24 + x^5/120 + x^6/720 + x^7/5040 +
x^8/40320 + x^9/362880 + 1)ただし、ただ合算しただけではCos関数とSin関数の合成関数を近似するのみである。
yacas("Taylor(x, 0, 9) Sin(x)+Cos(x)")
expression(x - x^2/2 - x^3/6 + x^4/24 + x^5/120 - x^6/720 - x^7/5040 +
x^8/40320 + x^9/362880 + 1)
Yacasで計算可能なのはここまで。
ここで「2乗すると-1になる複素数i」の概念を導入すると符号違いの問題が解決されてオイラーの公式Exp(xi)=Cos(x)+Sin(xi)が成立する。
- Exp(xi)=xi/1!+xi^2/2!+xi^3/3!+xi^4/4!+xi^4/5!+xi^6/6!+xi^7/7!+xi^8/8!+xi^9/9!…
- Exp(xi)=1+xi-x^2/2-xi^3/3!+x^4/4!+xi^5/5!-x^6/6!-xi^7/7!+x^8/8!+xi^9/9!…
- Exp(xi)=(1-x^2/2+x^4/4-x^6/6!+x^8/8!…)+(xi-xi^3/3!+xi^5/5!-xi^7/7!+ xi^9/9!…)
- Exp(xi)=Cos(x)+Sin(xi)
さらに「複素数平面」の概念を導入し、虚数部Sin(x)実数部Cos(x) をY軸に取ると円関数の近似過程が見受けられる。
まぁ、これからも使える機会があれば使っていきます。
*1:a * (-2 * b) + c)^2 - 4 * (a * (a * b^2 + d))) - (a * (-2 * b) + c" style="background-color: transparent; color: #5684d7; overflow-wrap: break-word; text-decoration: underline;">*7/(2 * a)
sqrt(15/2)
[1] 2.738613
sqrt(120)/4
[1] 2.738613
*計算が合ってない気がするがさて置く
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#円関数
yacas("Solve(Sqrt(x^2+y^2)-1,y)")
Yacas vector:
[1] y == root(abs(x^2 - 1), 2) * complex_cartesian(cos(argument(1 - x^2)/2), sin(argument(1 - x^2)/2*2:argument(1 - x^2) + 2 * pi)/2), sin((argument(1 - x^2) + 2 * pi)/2
*3:argument(1 - x^2) + 2 * pi)/2), sin((argument(1 - x^2) + 2 * pi)/2
*4:5-2)!)")
expression(20)#Rには順列を直接計算する函数はないので例えば相乗の函数prodを用いる。nPrはprod((n-r+1):n)と計算するが、この方法はr=0のときうまくいかない。
n<-5; r<-2
prod((n-r+1):n)
[1] 20
#なおRの場合、e1071というパッケージに含まれるpermutationsという函数は、引数にとった数までの順列のパターンをすべて表示してくれる。例えばpermutations(3)とすれば、1から3までの数をすべて1回ずつ使った場合、どういう並べ方があるかを教えてくれる。
library(e1071)
permutations(3)
[,1] [,2] [,3]
[1,] 1 2 3
[2,] 2 1 3
[3,] 2 3 1
[4,] 1 3 2
[5,] 3 1 2
[6,] 3 2 1
組み合わせ(combination, choose、nCr=nPr/r!)
異なるn個の中から異なるr個とる組み合わせの数の事。記号Cで表す。例えば5人(A、B、C、D、E)の中から2人を選ぶ組み合わせを考えると{AB}、{CD}、{AC}…のようになり合計10通り。{AB}と{BA}のチームを同じと考えるので順列の総数の半分となる。
#統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
#yacasでは組合せnCr=nPr/r!はBin(n,r) 。bin はbinomial coeffients(2項係数)から来ている。これは2項係数の係数がnCrだからである。
yacas("Bin(5,2)")
expression(10)#Rで組み合わせの数を求めるには函数chooseを用いる。 nCrを求めたければchoose(n, r)となる。
n<-5; r<-2
choose(n, r)
[1] 10
#なおRではcombnという函数を用いると、ありうる組み合わせのすべてを行列の形で表示させることができる。
people <- c("A", "B", "C", "D")
combn(people, 3)
[,1] [,2] [,3] [,4]
[1,] "A" "A" "A" "B"
[2,] "B" "B" "C" "C"
[3,] "C" "D" "D" "D"
日本の高等学校における数学の科目の一つである。
- 1994年4月施行版では数学Iとの並行履修、あるいは数学Iを履修した後に履修させ、4項目中2項目以上を選択履修させることとされた。
- 2003年4月施行版では原則として数学基礎または数学Iとの並行履修、あるいは数学基礎または数学Iを履修した後に履修させ、すべての項目を履修させることとされた。
- 2012年4月施行版では原則として数学Iとの並行履修、あるいは数学Iを履修した後に履修させ、3項目中2項目以上を選択履修させることとされている。
現行学習指導要領下での本科目は2012年度より学年進行で実施されている。
1章 数と式
統計言語Rでの汎用計算機代数ソフトウェアYacasによる計算例
library(Ryacas)
yacas("Expand((2*x^2+x+3)*(2*x-3*5:x+a)*(x+b
*6:a+b)*(a-b
*7:a+b)^2)")
expression(a^2 + 2 * (b * a) + b^2)
yacas("Expand((a-b)^2)")
expression(a^2 - 2 * (b * a) + b^2)
yacas("Expand((a*x+b)*(c*x+d*8:c * x^2 + d * x) * a + (c * b * x + d * b)
#乗法公式Ⅱ (高校数学範囲)
yacas("Expand((a+b)^3)")
expression(a^3 + 3 * (b * a^2) + 3 * (b^2 * a) + b^3)
yacas("Expand((a−b)^3)")
expression(a^3 - 3 * (b * a^2) + 3 * (b^2 * a) - b^3)
yacas("Expand((a+b)*(a^2-a*b+b^2*9:a-b)*(a^2+a*b+b^2
*10:a+b+c)^2)")
expression(a^2 + (2 * b + 2 * c) * a + (b^2 + 2 * (c * b) + c^2*11:a+b)^4)")
expression(a^4 + 4 * (b * a^3) + 6 * (b^2 * a^2) + 4 * (b^3 *
a) + b^4)
yacas("Expand((a-b)^4)")
expression(a^4 - 4 * (b * a^3) + 6 * (b^2 * a^2) - 4 * (b^3 *
a) + b^4)
#逆を言えば以下までは求められない。
yacas("Expand((a+b)^-2)")
expression((a + b)^-2)
#数学的に無意味なので全く解いてくれないが指数規則的に1/(a^2+2*a*b+b^2)では? パスカルの逆三角形…
yacas("Expand((a-b)^-2)")
expression((a - b)^-2)
#数学的に無意味なので全く解いてくれないが指数規則的に1/(x^2-2*a*b+b^2)では? パスカルの逆三角形…
yacas("Expand((a+b)^-1)")
expression((a + b)^-1)
#数学的に無意味なので全く解いてくれないが指数規則的に1/(a+b)では? パスカルの逆三角形…
yacas("Expand((a-b)^-1)")
expression((a - b)^-1)
#数学的に無意味なので全く解いてくれないが1/(a-b)では? パスカルの逆三角形…
yacas("Expand((a+b)^0)")
expression(1)
#(a+b)/(a+b)=1
yacas("Expand((a-b)^0)")
expression(1)
#(a-b)/(a-b)=1
yacas("Expand((a+b)/(a-b*12:a + b)/(a - b
*13:a+b)^1)")
expression(a + b)
yacas("Expand((a-b)^1)")
expression(a - b)
#三乗レベルにおける(x+y)と(x-y)の混在。係数(1,1)
yacas("Expand((x+y)^2*(x-y*14:x+y)*(x-y)^2)")
expression(x^3 - y * x^2 - y^2 * x + y^3)
#四乗レベルにおける(x+y)と(x-y)の混在。係数(1,2,2,1)(2,2)
yacas("Expand((a+b)*(a-b)^3)")
expression(a^4 - 2 * (b * a^3) + 2 * (b^3 * a) - b^4)
yacas("Expand((a+b)^2*(a-b)^2)")
expression(a^4 - 2 * (b^2 * a^2) + b^4)
yacas("Expand((a+b)^3*(a-b*15:a+b)^5)")
expression(a^5 + 5 * (b * a^4) + 10 * (b^2 * a^3) + 10 * (b^3 *
a^2) + 5 * (b^4 * a) + b^5)
yacas("Expand((a-b)^5)")
expression(a^5 - 5 * (b * a^4) + 10 * (b^2 * a^3) - 10 * (b^3 *
a^2) + 5 * (b^4 * a) - b^5)
*五乗レベルにおける(x+y)と(x-y)の混在。係数(3,2,2,3)(1,2,2,1)
yacas("Expand((a+b)*(a-b)^4)")
expression(a^5 - 3 * (b * a^4) + 2 * (b^2 * a^3) + 2 * (b^3 *
a^2) - 3 * (b^4 * a) + b^5)
yacas("Expand((a+b)^2*(a-b)^3)")
expression(a^5 - b * a^4 - 2 * (b^2 * a^3) + 2 * (b^3 * a^2) +
b^4 * a - b^5)
yacas("Expand((a+b)^3*(a-b)^2)")
expression(a^5 + b * a^4 - 2 * (b^2 * a^3) - 2 * (b^3 * a^2) +
b^4 * a + b^5)
yacas("Expand((a+b)^4*(a-b)^1)")
expression(a^5 + 3 * (b * a^4) + 2 * (b^2 * a^3) - 2 * (b^3 *
a^2) - 3 * (b^4 * a) - b^5)
*六乗
yacas("Expand((a+b)^6)")
expression(a^6 + 6 * (b * a^5) + 15 * (b^2 * a^4) + 20 * (b^3 *
a^3) + 15 * (b^4 * a^2) + 6 * (b^5 * a) + b^6)
yacas("Expand((a-b)^6)")
expression(a^6 - 6 * (b * a^5) + 15 * (b^2 * a^4) - 20 * (b^3 *
a^3) + 15 * (b^4 * a^2) - 6 * (b^5 * a) + b^6)*六乗レベルにおける(a+b)と(a-b)の混在。係数(4,5,5,4)(2,4,4,2)(3,3)
yacas("Expand((a+b)*(a-b)^5)")
expression(a^6 - 4 * (b * a^5) + 5 * (b^2 * a^4) - 5 * (b^4 *
a^2) + 4 * (b^5 * a) - b^6)
yacas("Expand((a+b)^2*(a-b)^4)")
expression(a^6 - 2 * (b * a^5) - b^2 * a^4 + 4 * (b^3 * a^3) -
b^4 * a^2 - 2 * (b^5 * a) + b^6)
yacas("Expand((a+b)^3*(a-b)^3)")
expression(a^6 - 3 * (b^2 * a^4) + 3 * (b^4 * a^2) - b^6)
yacas("Expand((a+b)^4*(a-b)^2)")
expression(a^6 + 2 * (b * a^5) - b^2 * a^4 - 4 * (b^3 * a^3) -
b^4 * a^2 + 2 * (b^5 * a) + b^6)
yacas("Expand((a+b)^5*(a-b*16:x+a)*(x+b)*(x+c
*17:b + c) * a + c * b) *
x + c * b * a)
yacas("Expand((a+b+c)*(a^2+b^2+c^2−a*b−b*c−c*a*18:c - b) * a^2 + (b^2 - c^2) * a + (c^2 * b - c * b^2
*19:a+b)*(b+c)*(c+a
*20:b + c) * a^2 + (b^2 + 2 * (c * b) + c^2) * a + (c *
b^2 + c^2 * b*21:a+b+c)^3)")
expression(a^3 + (3 * b + 3 * c) * a^2 + (3 * b^2 + 6 * (c *
b) + 3 * c^2) * a + (b^3 + 3 * (c * b^2) + 3 * (c^2 * b) +
c^3*22:a + 4) * (a + 3
*23:2 * x + 3) * (4 * x + 3) + 2 * (2 * x^2 + 3 * x -
1*24:3 * (x^2 + 1) - (3 * x - 1) * (2 * x
*25:-3 * x^2 + 2 * x + 3)/(x^4 + 2 * x^2 + 1
*26:a * x - c)/b)
#表現形式
yacas("{{a,b},{c,d}}")
Yacas matrix:
[,1] [,2]
[1,] a b
[2,] c dyacas("{{1,3},{5,-2}}")
Yacas matrix:
[,1] [,2]
[1,] 1 3
[2,] 5 -2yacas("{{1,3},{5,-2}}+{{6,-7},{4,8}}")
Yacas matrix:
[,1] [,2]
[1,] 7 -4
[2,] 9 6
yacas("2*{{1,2},{3,4}}")
Yacas matrix:
[,1] [,2]
[1,] 2 4
[2,] 6 8
yacas("{{800,700},{1000,500}} . {2,3}")
Yacas vector:
[1] 3700 3500
yacas("{{1,3},{6,7}} . {{2,0},{4,5}}")
Yacas matrix:
[,1] [,2]
[1,] 14 15
[2,] 40 35#零行列
yacas("ZeroMatrix(2,3)")
Yacas matrix:
[,1] [,2] [,3]
[1,] 0 0 0
[2,] 0 0 0
yacas("ZeroMatrix(2)")
Yacas matrix:
[,1] [,2]
[1,] 0 0
[2,] 0 0
#単位行列
yacas("Identity(n)")
expression(Identity(n