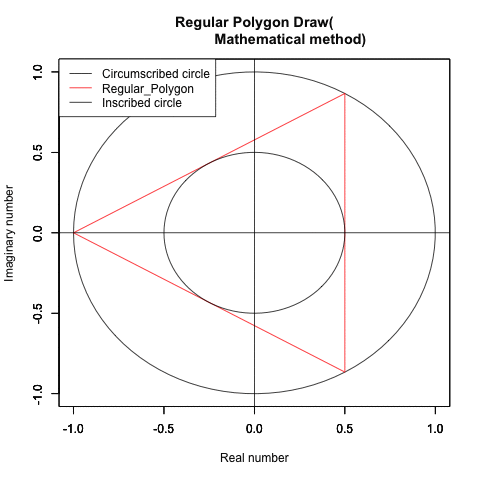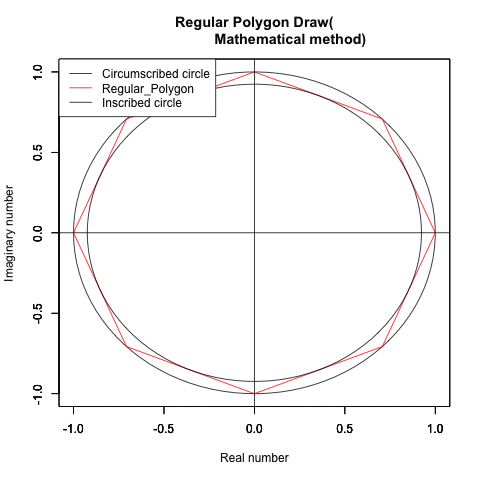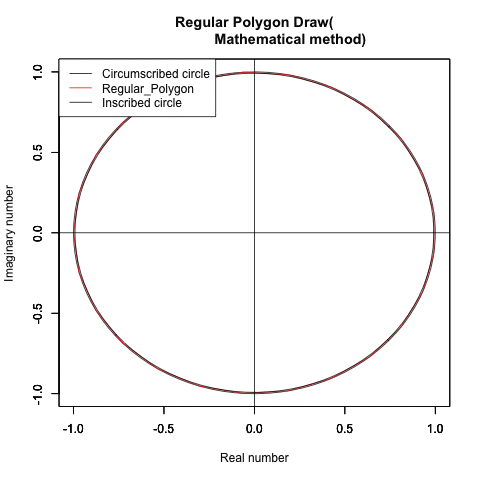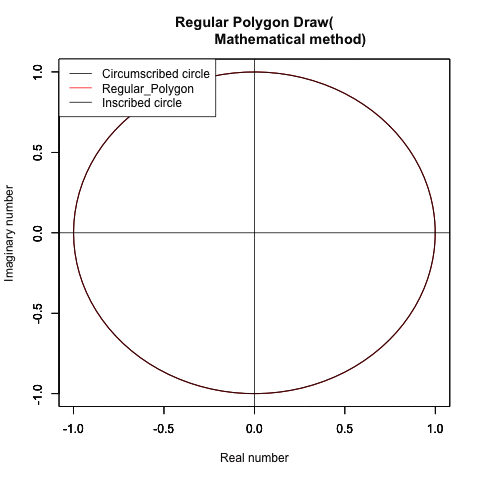
「対象円(Target circle)に外接(circumscribe)あるいは内接(inscribe)する正多角形(regular polygon)」と「その多角形に外接あるいは内接する円周(circle)」については以下の法則が成り立ちます。
一辺の長さがaの正n角形に外接する円の半径r
- r=a/(2*tan(pi/n))
- a=r*(2*tan(pi/n))
一辺の長さがaの正n角形に内接する円の半径R
- R=a/(2*tan(pi/n))/cos(pi/n)
- a=R*(2*tan(pi/n))/cos(pi/n)
一辺の長さがaの正n角形の外接円の半径と内接円の半径の関係
- r=R*cos(pi/n)
- R=r/cos(pi/n)
【注釈】この法則を上手く使えばa*nすなわち「対象円に外接する正n角形の全周」と「対象円に内接する正n角形の全周」で「半径1の円の全周=2*π(=6.283185…)」を挟み撃ちにする形で円周率「π(3.141593…)」をある程度の精度まで求められる筈である。要するに「対象円に内接する正n角形の一辺の長さ=a0」「対象円に外接する正n角形の一辺の長さ=a1」とすると「a1*n-a0*n」で近似していく。
それでは実際にやってみるとどんな具合になるか試してみましょう。各円周のサイズはnに対応する指数関数n^x(ただし-1>=x>=1)で示します。
①正1角形(pi=3.141593ラジアンあるいは360度)の場合…概ね「球面上において出発点と終点を等しくする円周(距離も不定なら円面積全体)もしくは球表面(距離も不定なら球体積全体)」として想像される。その外接円の内接円に対する半径の比率は1倍、すなわち円周のそれと一致する。
「一角形は1つの辺と1つの内角しかもたないため、定義より全ての一角形は正一角形になる。」(wikipedia:一角形)
— κねこせん (@necocen) August 25, 2013
- 2*tan(pi)=-2.449294e-16
*これは「0に限りなく近い」という意味。 - 2*tan(pi)/cos(pi)=2.449294e-16
*符号にかかわらずこれも同様。 - cos(pi)=-1
②正2角形(pi/2=3.141593ラジアンあるいは180度)の場合…概ね「任意の円弧を2分割する2点(直線距離1に対して円弧上の距離はπ/2倍)、あるいは出発地点と到着定点の間を等しい測地線で結ぶ球表面上の円弧を観測原点とその面幾何学においておける原点出発点と終点を等しくする円周もしくは球上の一点」を指す。例えば任意の球表面上において出発点「1」とその座標上正反対に位置する対蹠地「−1」の間を(両者の直線距離1に対してπ/2倍の距離で結ぶ)無数の測地線など。
直線の概念を曲がった空間において一般化したものである。測地線の中でその長さが2点間の距離に等しくなるものを最短測地線という。
言葉の由来は、測地学からであり、地球上の2点間の最短ルート(大円の一部)による。この概念は、数学的な空間にも拡張され、例えばグラフ理論ではグラフ上の2つの頂点(vertex)や結節点 (node) 間の測地線が定義されている。一般相対性理論では、光は曲がった空間での測地線を進むという原理に基づいて構築されている。
概要として、単純な例を示す。 地球を単純に球面であるとしよう.地球表面上で生活する我々は,例えば 東京とニューヨークの間を最短距離で移動するためには、東京とニューヨークを通る大円に沿った移動を行えばよく、この大円の一部こそ、測地線と呼ばれるものになる。
しかしながら、一般に、大円をその上の2点で分けると優弧と劣弧に分かれる。東京からニューヨークへ大円に沿った移動をしても、東京からニューヨークに行くには大円の周り方によって遠い移動と近い移動とある。この場合、劣弧に沿って移動すれば最短距離、優弧に沿えば直線的な移動としては最も遠回りになるわけである。大円の一部である弧は測地線となるが、必ずしも2点間の最短距離を示す曲線とはならない。
逆に2点間の最短距離を示す曲線は測地線となるので、2点を結ぶ測地線の中で最短のものが2点の最短距離を示すと考えてよい。その意味で、測地線というのは、2点間の最短距離を測るための曲線の候補の集まりであるともいえる。
ちなみに、2点を北極と南極のような対極の位置に取れば、この2点を結ぶ最短測地線は無数にあることにも注意されたい。
球面では測地線は閉曲線となるが、回転楕円体面上など一般には測地線は閉曲線とならない。
地球あるいは他の天体上で、ある場所とは180°逆に位置する場所。地球においては俗にいう「地球の裏側」である。対蹠点(たいせきてん、たいしょてん)とも言う。数学では3次元のいわゆる球以外の、抽象的な球面に対しても対蹠点という表現を使う。なお、対称点(たいしょうてん)は誤り。
「対蹠」の「蹠」は、「足裏」を意味する語である。従って、「対蹠」とは、「足裏を対する」という意味で、即ち「正反対」を意味する語である。英語の「antipode」は、“anti”(反対)と“pode”(足)の合成語で、「足を対した所」を意味する。日本で「蹠」を「しょ」と読むのは慣用読みであり、本来の漢音は「せき」である。

- 2*tan(pi/2)=3.266248e+16
*∞(無限大)とも。単位円の様な実数領域には存在し得ない値。オイラーの等式「e^πi=-1」によって「1+πi」が究極的には「-1+0i」と等価とされる複素数表示だと「1+1i」となる。

- 2*tan(pi/2)/cos(pi/2)=2.667094e+32
*∞(無限大)/0とかそういう感じで定義不可。 - cos(pi/2)=6.123234e-17
*これは「0に限りなく近い」という意味。
③正三角形(Equilateral triangle, pi/3=1.047198ラジアンあるいは60度)の場合
対象円に内接する正三角形の高さ(内接円の半径r*3)をh(height)とする。外接円の内接円に対する半径の比率は指数サイズ1すなわち対数比(...1/root^x,1/root,root/root,root,root^x...)で推移し平面充填性(同じ図面で平面を埋め尽くす能力)に加え空間充填性(同じ立体で空間を埋め尽くす能力)も備える。立体としては正四面体(Regular tetrahedron, 辺数6、頂点数4)を構成し、その表面積はsqrt(2)*a^2、体積はsqrt(2)/12*a^3で表される。正八面体(Regular octahedron, 辺数12、頂点数6、表面積2*sqrt(2)*a^2、体積sqrt(2)/3*a^3)や正二十面体(regular icosahedron、辺数30、頂点数12、表面積5*sqrt(2)*a^2、体積12/5*(3+sqrt(5))*a^3)とは双対の関係にある。

- 2*tan(pi/3)=3.464102
- 2*tan(pi/3)/cos(pi/3)=6.928203
- cos(pi/3)=1/2=0.5
一辺の長さがaの正3角形に内接する円の半径r
- r=a*(2*tan(pi/3))=a*3.464102
- a=r/(2*tan(pi/3))=r/3.464102
一辺の長さがaの正3角形に外接する円の半径R
- R=a/(2*tan(pi/3))/cos(pi/3)=a/6.928203
- a=R*(2*tan(pi/3))/cos(pi/3)=R*6.928203
一辺の長さがaの正3角形の外接円の半径と内接円の関係
- r=R*cos(pi/3)=R/2
- R=r/cos(pi/3)=2r
結果はなんと「7.348469<=π<=10.3923」で「不正解」範囲…
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 3^-1 | 3^-1(3^0r) | 1/2=0.5 |
| 2 | 3^-1 | 3^-1h=3^-1*3 | 3/2=1.5 |
| 3 | 3^-1 | 3^-1a1=3^0a0 | 2*sqrt(1.5)=2.44949 |
| 4 | 3^-1 | 3^-1a1(3^0a0)*3 | 6*sqrt(1.5)=7.348469 |
| 5 | 3^0 | 3^0(3^-1R,3^1r) | 1.0 |
| 6 | 3^0 | 3^0h=3^0*3 | 3.0 |
| 7 | 3^0 | 3^0a1=3^1a0 | 2*sqrt(3)=3.464102 |
| 8 | 3^0 | 3^0a1(3^1a0)*3 | 6*sqrt(3)=10.3923 |
| 9 | 3^1 | 3^1(3^0R) | 3.0 |
④正方形(Square, pi/4=0.7853982ラジアンあるいは45度)の場合
対象円に内接する正方形の対角線(外接円の一辺の長さ)をd(diagonal)とする。外接円に対する内接円の半径の比率は指数サイズ0.5すなわち対数比の半分(...1/root^x,,1/root,2/sqrt(root),root/root,sqrt(root),root,2*sqrt(root),root^x...)で推移し平面充填性(同じ図面で平面を埋め尽くす能力)に加え空間充填性(同じ立体で空間を埋め尽くす能力)も備える。立体としては正六面体(Regular tetrahedron, 辺数12、頂点数8)を構成し、その表面積は6*a^2、体積はa^3で表される。
- 2*tan(pi/4)=2
- 2*tan(pi/4)/cos(pi/4)=2.828427
- cos(pi/4)=0.7071068
一辺の長さがaの正方形に内接する円の半径r
- r=a*(2*tan(pi/4))=a/2
- a=r/(2*tan(pi/4))=r*2
一辺の長さがaの正方形に外接する円の半径R
- R=a/(2*tan(pi/4))/cos(pi/4)=a/2.828427
- a=R*(2*tan(pi/4))/cos(pi/4)=R*2.828427
一辺の長さがaの正方形の外接円の半径と内接円の関係
- r=R*cos(pi/4)=R/2
- R=r/cos(pi/4)=2r
結果は「5.656854<=π<= 8」で正解範囲…
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 2^-1 | 2^-1(2^-0.5r) | 0.5 |
| 2 | 2^-1 | 2^-1d=2^-1*4 | 1 |
| 3 | 2^-1 | 2^-1a1=2^0a0 | sqrt(2)=1.414214 |
| 4 | 2^-1 | 2^-1a1(2^-0.5a0)*4 | 4sqrt(2)=5.656854 |
| 5 | 2^-0.5 | 2^-0.5(2^0r) | sqrt(2)/2=0.7071068 |
| 6 | 2^-0.5 | 2^-0.5d=2^-0.5*4 | sqrt(2)=1.414214 |
| 7 | 2^-0.5 | 2^-0.5a1=2^0a0 | 1 |
| 8 | 2^-0.5 | 2^-1a1(2^0.5a0)*4 | 4 |
| 9 | 2^0 | 2^0(2^-0.5R,2^0.5r) | 1 |
| 10 | 2^0 | 2^0d=2^0*4 | 2 |
| 11 | 2^0 | 2^0a1=2^0.5a0 | sqrt(8)=2sqrt(2)=2.828427 |
| 12 | 2^0 | 2^0a1(2^0.5a0)*4 | sqrt(32)=4sqrt(2)=5.656854 |
| 13 | 2^0.5 | 2^0.5(2^-0R,2^1r) | sqrt(2)=1.414214 |
| 14 | 2^0.5 | 2^0.5d=2^0.5*4 | 2sqrt(2)=2.828427 |
| 15 | 2^0.5 | 2^0.5a1=2^1a0 | 4 |
| 16 | 2^0.5 | 2^0.5a1(2^0a0)*4 | 8 |
| 17 | 2^1 | 2^1(2^1-0.5R,2^0.5r) | 2 |
⑤正五角形(Regular pentagon、pi/5=>0.6283185ラジアンあるいは36度)の場合
対象円に内接する正五角形の対角線(1+sqrt(5))/2)をd(diagonal)とする。外接円に対する内接円の半径の比率は指数サイズで推移せず(0.809017倍)、空間充填性(同じ立体で空間を埋め尽くす能力)は備えるも平面充填性(同じ図面で平面を埋め尽くす能力)は備えない。立体としては正12面体(Rregular dodecahedron, 辺数30、頂点数20)を構成し、その表面積は3*sqrt(25+10*sqrt(5))*a^2、体積は(15+7*sqrt(5))/4*a^3で表される。

- 2*tan(pi/5)=1.453085
- 2*tan(pi/5)/cos(pi/5)=1.796112
- cos(pi/5)=0.809017
一辺の長さがaの正五角形に内接する円の半径r
- r=a*(2*tan(pi/5))=a*1.453085
- a=r/(2*tan(pi/5))=r/1.453085
一辺の長さがaの正五角形に外接する円の半径R
- R=a/(2*tan(pi/5))/cos(pi/5)=a/1.796112
- a=R*(2*tan(pi/5))/cos(pi/5)=R*1.796112
一辺の長さがaの正五角形の外接円の半径と内接円の関係
- r=R*cos(pi/5)=R*0.809017
- R=r/cos(pi/5)=r/0.809017
結果は「3.440955<=π<=8.98056」で正解範囲…
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 5^-1 | 5^-1 | 1/5=0.2 |
| 2 | 5^-1 | 5^-1d | (1+sqrt(5))/2*0.2=0.3236068 |
| 3 | 5^-1 | 5^-1a1 | 0.2*1.796112=0.3592224 |
| 4 | 5^-1 | 5^-1a1*5 | 0.3592224*5=1.796112 |
| 5 | 5^-0.2722623 | 5^-0.2722623 | 0.3592224*1.796112=-0.2722623 |
| 6 | ... | ... | ... |
| 7 | 5^-0.131683 | 5^-0.131683 | 0.8090168 |
| 8 | 5^0 | 5^0a0 | 1/1.453085=0.688191 |
| 9 | 5^0 | 5^0a0*5 | 0.5567581*5=3.440955 |
| 10 | 5^0 | 5^0=1 | 1.0 |
| 11 | 5^0 | 5^0d | (1+sqrt(5))/2=1.618034 |
| 12 | 5^0 | 5^0a1 | 1.796112 |
| 13 | 5^0 | 5^0a1*5 | 1.796112*5=8.98056 |
| 14 | 5^0.1316829 | 5^0.7277376 | 1.796112*1.796112=3.226018 |
| 15 | ... | ... | ... |
| 16 | 5^0.535628 | 5^0.535628 | 3.440955*1.453085=2.368034 |
| 17 | 5^1 | 5^0a1 | 5/1.453085=3.440955 |
| 18 | 5^1 | 5^0a1*5 | 3.440955*5=17.20478 |
| 19 | 5^1 | 5^1 | 5 |
| 20 | 5^1 | 5^1d | *1/2)*5=8.09017 |
⑥正六角形(pi/6=0.5235988ラジアンあるいは60度)の場合
対象円の半径と内接する正六角形の1辺の長さが一致する。外接円に対する内接円の半径の比率は指数サイズで推移せず(0.8660254倍)、空間充填性(同じ立体で空間を埋め尽くす能力)は備えないが平面充填性(同じ図面で平面を埋め尽くす能力)は備える。
*平面充填性(同じ図面で平面を埋め尽くす能力)は備える。…まぁ平面上は「正三角形を6個寄せ集めたもの」なので当然といえば当然。これも双対関係の1種?


- 2*tan(pi/6)=1.154701
- 2*tan(pi/6)/cos(pi/6)=1.333333
- cos(pi/6)=0.8660254
一辺の長さがaの正6角形に内接する円の半径r
- r=a*(2*tan(pi/6))=a*1.154701
- a=r/(2*tan(pi/6))=r/1.154701
一辺の長さがaの正6角形に外接する円の半径R
- R=a/(2*tan(pi/6))/cos(pi/6)=a/1.333333
- a=R*(2*tan(pi/6))/cos(pi/6)=R*1.333333
一辺の長さがaの正3角形の外接円の半径と内接円の関係
- r=R*cos(pi/6)=R*0.8660254
- R=r/cos(pi/6)=r/0.8660254
結果は「6<=π<=7.999998」で正解範囲。概ね古代エジプトやバビロニア、インド、ギリシアの幾何学者達が挟み撃ち法で円周率を求める時はこの辺りから出発している。
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 6^-1 | 6^-1 | 1/6=0.1666666 |
| 2 | 6^-1 | 6^-1a1 | 1/6*1.154701=0.1924502 |
| 3 | 6^-1 | 6^-1a1*6 | 0.1924502*6=1.154701 |
| 4 | 6^-0.8394411 | 6^-0.8394411 | 0.1924502*1.154701=0.2222224 |
| 5 | ... | ... | ... |
| 6 | 6^-0.08027941 | 6^-0.08027921 | -0.8660254 |
| 7 | 6^0 | 6^0a0 | 1.0 |
| 8 | 6^0 | 6^0a0*6 | 6.0 |
| 9 | 6^0 | 6^0 | 1.0 |
| 10 | 6^0 | 6^0a1 | 1.333333 |
| 11 | 6^0 | 6^0a1*6 | 1.333333*6=7.999998 |
| 12 | 6^0.08027895 | 6^0.08027895 | 1.333333*0.8660254=1.333334 |
| 13 | ... | ... | ... |
| 14 | 6^0.7591625 | 6^0.7591625 | 4.500001*0.8660254=3.897115 |
| 15 | 6^1 | 6^1a0 | 6/1.333333=4.500001 |
| 16 | 6^1 | 6^1a0*6 | 4.500001*6=27.00001 |
| 17 | 6^1 | 6^1 | 6.0 |
⑦正7角形(pi/7=0.448799ラジアンあるいは51.42857度)の場合
人間にとって有意味な特徴を一切備えていないので無視されがち。そもそも三角定規やコンパスで正確に作図出来ない。

- 2*tan(pi/7)=0.9631492
- 2*tan(pi/7)/cos(pi/7)=1.069015
- cos(pi/7)=0.9009689
一辺の長さがaの正7角形に内接する円の半径r
- r=a*(2*tan(pi/7))=a*0.9631492
- a=r/(2*tan(pi/7))=r/0.9631492
一辺の長さがaの正7角形に外接する円の半径R
- R=a/(2*tan(pi/7))/cos(pi/7)=a/1.069015
- a=R*(2*tan(pi/7))/cos(pi/7)=R*1.069015
一辺の長さがaの正3角形の外接円の半径と内接円の関係
- r=R*cos(pi/7)=R*0.9009689
- R=r/cos(pi/7)=r/0.9009689
結果は「6.742045<=π<=7.483105」で正解範囲。概ね古代エジプトやバビロニア、インド、ギリシアの幾何学者達が挟み撃ち法で円周率を求める時はこの辺りから出発している。
| Target_size | Target_names | Target_values | |
|---|---|---|---|
| 1 | 7^-1 | 7^-1 | 1/7=0.1428571 |
| 2 | 7^-1 | 7^-1a1 | 0.1428571*1.069015=0.1527164 |
| 3 | 7^-1 | 7^-1a1*7 | 0.1527164*7=1.069015 |
| 4 | 7^-0.9464085 | 7^-0.9464085 | 0.1428571/0.9009689=0.1585594 |
| 5 | ... | ... | ... |
| 6 | 7^-0.05359165 | 7^-0.05359165 | 0.9009689 |
| 7 | 7^0 | 7^0a0 | 0.9009689*1.069015=1*0.9631492=0.96314933 |
| 8 | 7^0 | 7^0a0*7 | 6.742045 |
| 9 | 7^0 | 7^0 | 1.0 |
| 10 | 7^0 | 7^0a1 | 1.069015 |
| 11 | 7^0 | 7^0a1*7 | 1.069015*7=7.483105 |
| 12 | 7^0.05359155 | 7^0.05359155 | 1/0.9009689=1.109916 |
| 13 | ... | ... | ... |
| 14 | 7^0.9464083 | 7^0.9464083 | 7*0.9009689=6.306782 |
| 15 | 7^1 | 7^1a0 | 6/1.333333=4.500001 |
| 16 | 7^1 | 7^1a0*7 | 4.500001*6=27.00001 |
| 17 | 7^1 | 7^1 | 7.0 |
ここから読み取れる事。
①外接円に対する内接円の半径の比率はCos(π/n)で推移し、究極的には円のそれ、すなわち1倍(Cos(0))と合致する。
②この過程を外接円と内接円に挟まれた正多角形の側から見るとこうなる。
- この意味合いにおいて2πで表される円弧(あるいはそれを真横から見た地平線)には透視図法における消失点、すなわちある種の「事象の地平線(Event horizon)」性があるといえる。
- こうした振る舞いの背後に指数・対数関数的秩序や対数螺旋などの摂理が垣間見えるが、実数の世界には位相幾何学(Topology)やグラフ理論(Graph theory)の出発点となったオイラーの多面体定理、すなわち「穴の開いていない多面体、すなわち球面に位相同型な多面体については、頂点、辺、面の数について(頂点の数)-(辺の数)+ (面の数) = 2が成り立つ」に従う図形や立体のみが存在を許される。ただし「最適解のみが集中して現れるのはニュートン物理学サイズの世界のみ(量子力学サイズの世界では可能解全てを意識しなければならない)」とするファインマンの経路積分(Path integral)に照会すると、また違った答えが得られるかもしれない。
いずれにせよ生物界やデザインの世界はともかく、人類は空間分割認識の手段として平面充填性(同じ図面で平面を埋め尽くす能力)も空間充填性(同じ立体で空間を埋め尽くす能力)も備えた正三角形/四面体や正方形/六面体、平面充填性を備えた正六角形を主に選考していく道を選びます。そしてその結果、地図などの分野でそれらを「円の性質」とどう適合させていくかについて頭を悩まされる事になったのです。
*1:1+sqrt(5