統計言語Rによる検証例
#半径rの円の面積(pi*r^2)をrで微分(Differential)すると円周の長さ(2*pi*r)となる。
D01<-expression(pi*r^2)
D(D01,"r")
pi * (2 * r)#半径rの球の体積(4/3*pi*r^3)をrで微分(Differential)すると球の表面積(4*pi*r^2)となる。
D02<-expression(4/3*pi*r^3)
D(D02,"r")
4/3 * pi * (3 * r^2)
汎用計算機代数ソフトウェア"Yacas"による検証例
GNU General Public License にしたがった利用と配布が認められている汎用計算機代数アプリケーションのフリーソフトウェア。名前は Yet Another Computer Algebra System から来ている。
計算機代数の演算を行うシステムであるため、数式の記号操作ができる。また記号計算および任意精度の数値計算を行うための独自のプログラミング言語処理系を備えている。多くの数式処理操作を実装したスクリプトのライブラリを持っており、新たに実装したアルゴリズムの追加が容易に行えるようになっている。スクリプト言語および実装されている機能とアルゴリズムについての文書が多数用意されている。
ライブラリRyacasを使用した統計言語Rでの実証例
#ライブラリ読み込み
library(Ryacas)#半径rの球の体積(4/3*pi*r^3)をrで微分(Differential)すると球の表面積(4*pi*r^2)となる。
yac("D(r) 4/3 * pi * r^3")
[1] "r^2*4*pi"#逆に球の表面積(4*pi*r^2)をrで積分(Integrate)すると半径rの球の体積(4/3*pi*r^3)となる。
yac("Integrate(r) r^2 * (4 * pi)")
[1] "(r^3*4*pi)/3"
#半径rの円の面積(pi*r^2)をrで微分(Differential)すると円周の長さ(2*pi*r)となる。
yac("D(r) pi * r^2")
[1] "pi*2*r"
#逆に円周の長さ(2*pi*r)をrで積分(Integrate)すると半径rの円の面積(pi*r^2)になる。
yac("Integrate(r) pi * (2 * r)")
[1] "pi*r^2"
この数理モデルにおける半径rの球の体積と球の表面積の関係は「同心球の積層」 、円の面積と円周の長さの関係は「同心円の積層」というイメージ。
「オイラーの原始量(Euler's primitive sweep)」は、それこそ人間未満の生物に起源を有する様な粗雑な思考様式なので「とりあえず長さ1とみなした棒をグルグル振り回すと、その先端が円や球を描く」くらいの考え方しか出来ません。
統計言語Rによる作画例(線分から円の面積へ)複素数
#複素平面(球面)
Circle_Divide<-60 #円分割数Complex_plane01<-function(x){
#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- seq(0,2*pi,length=Circle_Divide)
cercle01<-exp(theta*(0+1i))
crcl_r<-Re(cercle01)
crcle_i<-Im(cercle01)
#塗りつぶし準備
segC<-rgb(0,1,0)
#円弧描写
plot(crcl_r, crcle_i,asp=1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="From Radius to Circle", xlab="Real numbers", ylab="Imaginary numbers")#インジケーターと塗り潰し
segments(crcl_r[x],crcle_i[x],0,0,col=segC)
polygon(c(crcl_r[1:x],0), #x
c(crcle_i[1:x],0), #y
density=c(30), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=segC) #塗りつぶす色}
#アニメーションさせてみる。
library("animation")
TC00=seq(0,2*pi,length=30)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
Time_Code<-TC01[TC01>=1 & TC01<=60 ]
saveGIF({
for (i in Time_Code){
Complex_plane01(i)
}
}, interval = 0.1, movie.name = "FRC01.gif")

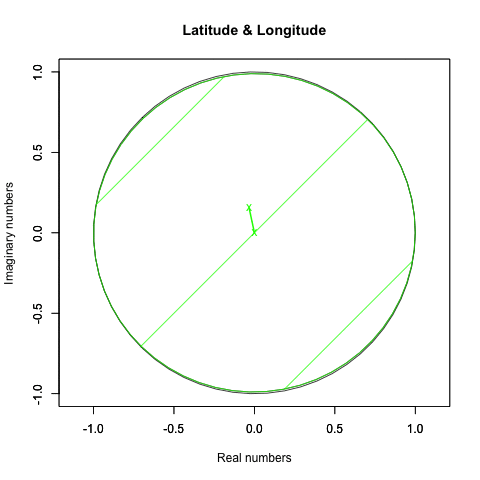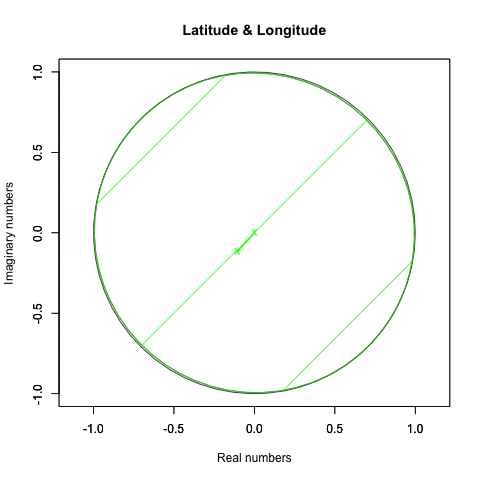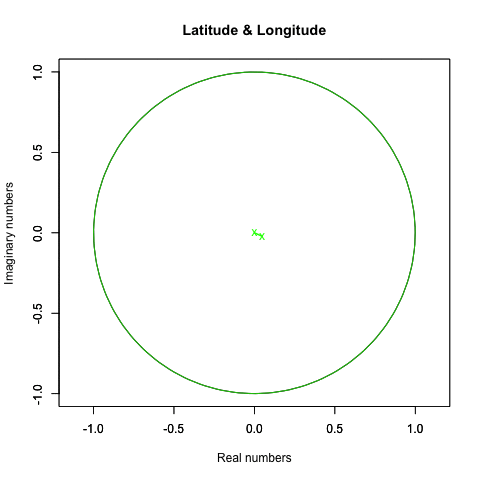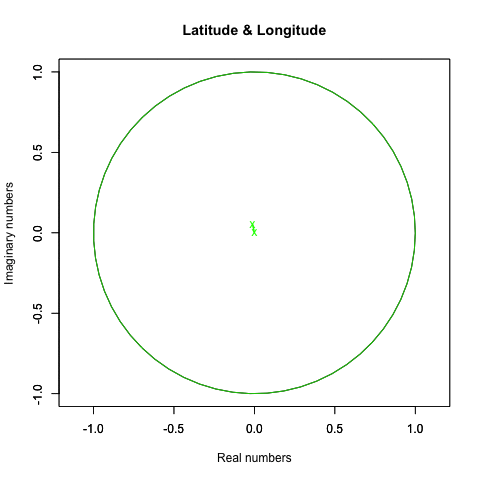
統計言語Rによる作画例(緯度と経度の回転)
#複素平面(球面)
Circle_Divide<-60 #円分割数
Complex_plane01<-function(x){#グラフのスケール決定
Graph_scale_x<-c(-1,1)
Graph_scale_y<-c(-1,1)
#円弧描写の準備
theta <- seq(0,2*pi,length=Circle_Divide)
cercle01<-exp(theta*(0+1i))
crcl_r<-Re(cercle01)
crcl_i<-Im(cercle01)#XY軸沿いの回転
xy_radian<-Re(x)
XY_Rotation_ratio<-cos(2*xy_radian/Circle_Divide*2*pi)/2+0.5
XYR_cos=crcl_r
XYR_sin=crcl_i*XY_Rotation_ratio#塗り潰し色(「右」が緑、「左」が赤)
ifelse*1
#Z軸沿いの回転
z_radian<-Im(x)
Z_Rotation_ratio<-z_radian/Circle_Divide*pi*2
XYZ_Rotation<-complex(real=XYR_cos,imaginary=XYR_sin)*(cos(Z_Rotation_ratio)+sin(Z_Rotation_ratio)*(0+1i))
XYZ_Rotation_cos<-Re(XYZ_Rotation)
XYZ_Rotation_sin<-Im(XYZ_Rotation)#Z軸沿いの回転(インジケーター)
ing<-complex(real=0,imaginary=crcl_i[xy_radian])*(cos(Z_Rotation_ratio)+sin(Z_Rotation_ratio)*(0+1i))
Ing_r<-Re(ing)
Ing_i<-Im(ing)#円弧描写
plot(crcl_r, crcl_i,asp=1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",col=rgb(0,0,0), main="Latitude & Longitude", xlab="Real numbers", ylab="Imaginary numbers")
par(new=T)#上書き指定#円弧の描写(回転)
plot(XYZ_Rotation_cos,XYZ_Rotation_sin,asp=1,xlim=Graph_scale_x,ylim=Graph_scale_y,type="l",main="", xlab="", ylab="")
segments(Ing_r,Ing_i,0,0,col=LR_color,lwd=2)
text(Ing_r,Ing_i,"x",col=LR_color)
text(0,0,"x",col=LR_color)
#円の塗り潰し
polygon(XYZ_Rotation_cos, #x
XYZ_Rotation_sin, #y
density=c(50*(1-XY_Rotation_ratio)), #塗りつぶす濃度
angle=c(45), #塗りつぶす斜線の角度
col=LR_color) #塗りつぶす色
}
X軸のみ回す。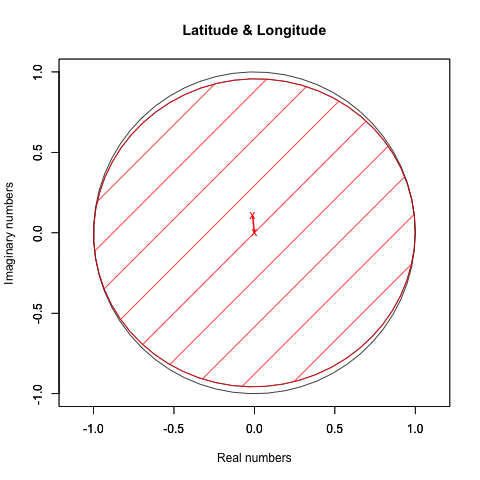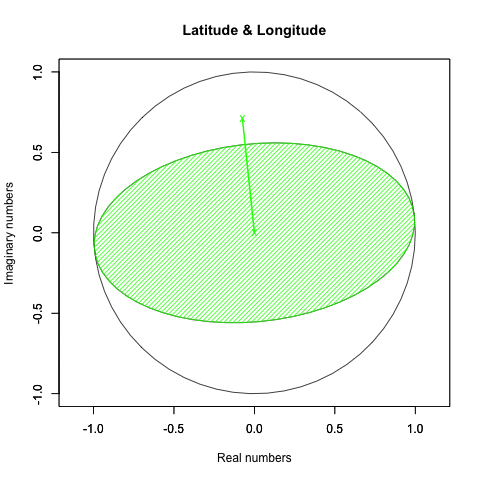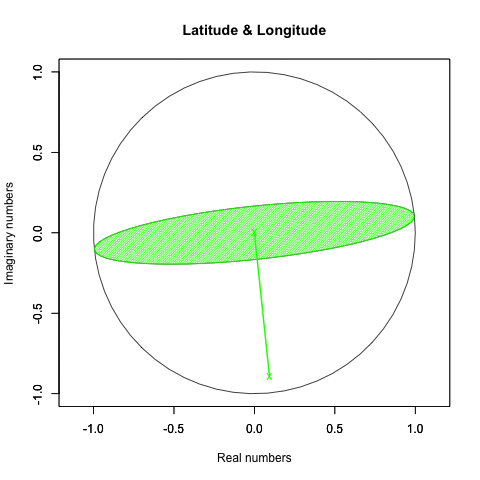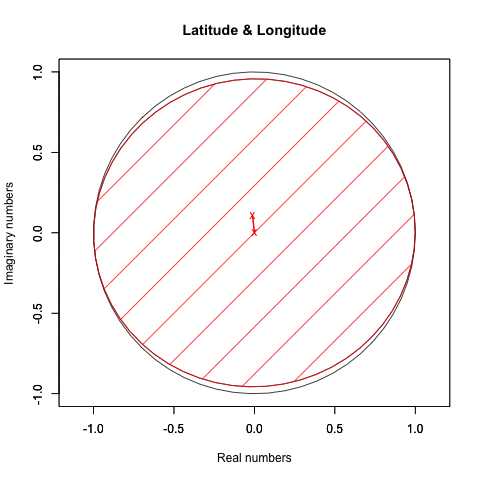
Y軸のみ回す。
library("animation")
#アニメーションさせてみる。
TC00=seq(0,2*pi,length=Circle_Divide/2)
TC01<-round(TC00/(2*pi)*Circle_Divide, digits = 0)
TC02<-TC01[TC01>=1 & TC01<=Circle_Divide ]
Time_Code<-complex(re=TC02, im=rep(Circle_Divide/4,length=Circle_Divide/2))
saveGIF({
for (i in Time_Code){
Complex_plane01(i)
}
}, interval = 0.1, movie.name = "LaLo02.gif")

Z軸のみ回す(ジンバルロック問題のせいで回って見えない)。
ここで合わせ技を投入?
*1:xy_radian%/%(Circle_Divide/4)==1 ||xy_radian%/%(Circle_Divide/4)==2),LR_color<-rgb(1,0,0),LR_color<-rgb(0,1,0









